«Геометрия показалась мне очень интересной и какой-то волшебной наукой». Это слова Архимеда, древнегреческого математика, физика и инженера из Сиракуз. Я полностью согласен со словами Архимеда, так как мне решение задач по геометрии доставляет удовольствие. Лично мне нравятся задачи, решение которых требует исследовательской работы. Поэтому, чтобы не тратить силы на знакомство с условием нескольких задач, достаточно рассмотреть решение только одной задачи, интересной по содержанию, богатой идеями, имеющей несколько способов решения.
Актуальность темы моей работы определяется необходимостью уметь решать задачи при сдаче ЕГЭ. Большинство задач по планиметрии не решается с помощью жестких алгоритмов, почти каждая требует своего подхода. В математике известно множество методов решения разных задач, к ним относятся: [3]
Ø Методы с использованием дополнительных построений.
Ø Методы, основанные на подобии треугольников.
Ø Методы, использующие соотношение между углами и сторонами прямоугольного треугольника.
Ø Координатный метод.
Ø Методы, использующие векторный аппарат.
Ø Проблема исследования заключается в изучении различных методов решения планиметрических задач и нахождении задач, решаемых разными методами, для того чтобы качественно подготовиться к ЕГЭ.
Объектом исследования являются геометрические задачи из раздела «Планиметрия».
Предметом исследования являются различные методы решения.
Гипотеза состоит в том, что изучать различные методы решения геометрических задач лучше на примере одной задачи, если она будет иметь их несколько.
Цель исследования – показать многообразие подходов при решении одной геометрической задачи и найти более рациональный способ решения задачи. Для достижения поставленной цели необходимо решить следующие задачи:
Ø изучить литературу по данной теме;
Ø исследовать разнообразные методы решений планиметрических задач;
Ø найти и решить геометрическую задачу всеми возможными изученными методами;
Ø проанализировать и сравнить полученные решения с целью нахождения наиболее эффективного подхода;
Ø создать устный журнал «Почти вся планиметрия в одной задаче».
Ø Предлагаемая исследовательская работа посвящена изучению различных методов решения одной задачи планиметрии.
Методы, использующие дополнительные построения.
При решении геометрических задач обычно используются три основных метода: геометрический – когда требуемое утверждение выводится с помощью логических рассуждений из ряда известных теорем; алгебраический – когда искомая геометрическая величина вычисляется на основании различных зависимостей между элементами геометрических фигур непосредственно или с помощью уравнений; комбинированный – когда на одних этапах решение ведется геометрическим методом, а на других – алгебраическим. Итак, я предлагаю следующую задачу решить различными методами и посмотреть, сколько получиться способов.
Задача. В трапеции диагонали длиной 6 см и 8 см взаимно перпендикулярны. Найти длину средней линии трапеции.
Методы дополнительного построения.
Способ №1 (построение прямой, параллельной диагонали). 1. Продолжим BC вправо. Проведем DK || AC. Так как ACKD – параллелограмм, то DK = 6 см.
2. BD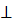 
DK, так как BD 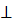AC. 
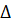BDK – прямоугольный.
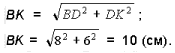
3. BK = BC + AD. Средняя линия равна половине BK, т. е. 5 см. Способ №2 (похожий на способ 1) Проведем CE || BD до пересечения с продолжением AD. DE = BC, так как DBCE – параллелограмм. AE вычислим по теореме Пифагора из 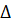ACE (CE || BD, но BD 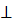AC, следовательно, CE 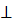AC):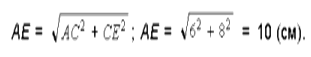 
AE = a + b. Но средняя линия равна: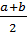 
т. е. равна 5 см. Ответ: 5 см.
Способ №3 (построение средних линий треугольников).
1. MN – средняя линия трапеции. Проведем MK || BD и соединим точки N и K.
2. NK – средняя линия ΔACD, следовательно, NK =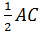
, NK=3cм
3. MK – средняя линия ΔABD, следовательно, MN =
BD, MK=4см
4. MKN = ΔAOD, как углы с соответственно параллельными сторонами.
5. ΔMNK прямоугольный.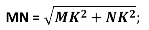 
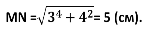
Ответ: 5 см.
Способ №4 (построение середин сторон трапеции).
Соединим середины сторон трапеции. Легко доказать, что MPNQ – параллелограмм с прямым углом, т. е. прямоугольник со сторонами 3 см и 4 см. Диагонали его MN = PQ = 5 см (египетский треугольник). Ответ: 5 см.
Способ № 5 (применение признаков равенства треугольников).
1.Продолжим CA на расстояние AM = CO. Через точку M проведем MN || AD. BD∩MN = N.
2. ΔOMN – прямоугольный, OM = 6 см, ON = 8 см. Следовательно, MN = 10 см (теорема Пифагора).
3. Проведем MK || ND. Продолжим AD до пересечения с MK. ΔMAK = ΔBOC (по I признаку), следовательно, AK = BC.
4. MKDN – параллелограмм, DK = MN = 10 см. Но DK = AD + BC.
Значит, средняя линия равна 5 см.
Ответ: 5 см.
Способ № 6 (применение признаков равенства треугольников). Продолжим AC за точку A так, что AM = OC. Продолжим BD за точку D так, что DN = BO. Итак, ΔOMN – прямоугольный с катетами 6 см и 8 см. По теореме Пифагора MN = 10 см. Проведем AE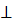 
MN, DF 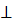MN, OK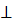BC.
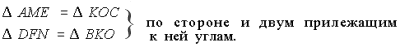Следовательно, ME = KC и FN = BK, т. е. MN = AD + BC = 10 (см).
Средняя линия равна: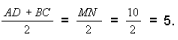 
Ответ: 5 см.
Способ №7 (Метод высот).
1.
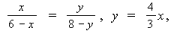
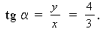
2. Из ΔACE: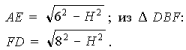 
3. 
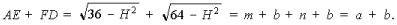
Средняя линия: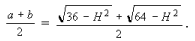 
(*)
4. Из ΔACE: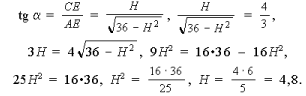 
5. Подставив в (*), находим: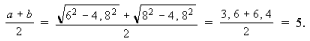 
Ответ: 5см.
Векторный метод.
Применение критериев коллинеарности векторов при решении задач. Переход от векторных равенств к скалярным происходит на основе единственности разложения вектора по двум неколлинеарным векторам.
Способ № 8 (с использованием векторного аппарата).
точки M и N – середины сторон BC и AD. Можно доказать, что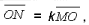 
т. е. векторы коллинеарны и точки M, O, N лежат на одной прямой. Известно, что
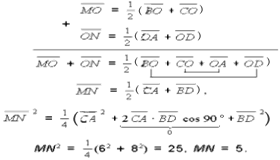
Используя предыдущий способ, легко показать, что MN равно длине средней линии в этой трапеции.
Ответ: 5 см. Способ №9 (с использованием векторного аппарата).
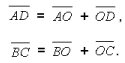
Сложим эти равенства почленно:
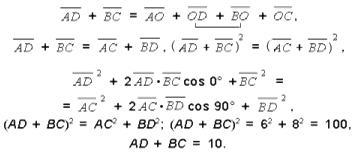
Но средняя линия равна полусумме AD и BC, т. е. 5 см. Ответ: 5 см.
Метод, основанный на подобии треугольников
Способ № 10
Пусть OC = x, BO = y; тогда AO = 6 – x, DO = 8 – y. MN – средняя линия.
1. Из подобия ΔBOC и ΔAOD имеем:
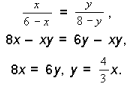
2. Из прямоугольного треугольника BOC имеем: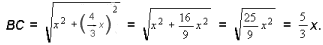 
3. Из подобия ΔBOC и ΔAOD имеем:
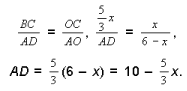
4.
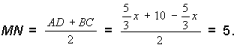
Ответ: 5 см.
Способ №11. 1. Из подобия ΔBOC и ΔAOD: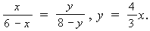
2. Продолжим диагонали на отрезки, равные CO и BO.
3. Из ΔMON: MN = 10 см.
4. ΔAOD подобен ΔMON;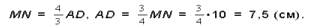
5. В ΔBOC: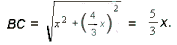 
6. ΔBOC подобен ΔAOD.
7.
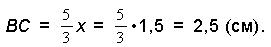
8. Средняя линия равна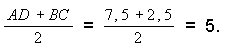 
Ответ: 5 см.
Метод введения вспомогательного неизвестного
Способ №12.
Пусть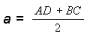 
– средняя линия.
OC = x, BO = y, OA = 6 – x, OD = 8 – y. Из подобия ΔBOC и ΔAOD:
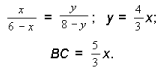
Пусть x < 3 (половины AC).
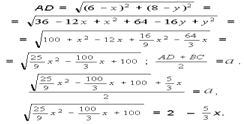
Возведем в квадрат: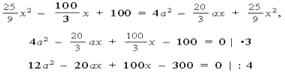
3a2 – 5ax + 25x – 75 = 0. Решим относительно a:
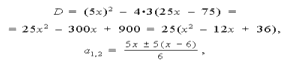
Ответ: 5 см.
Методы, использующие соотношение между углами и сторонами треугольника
Метод применения тригонометрии к решению геометрических задач
состоит в составлении формулы выражающей зависимость искомых отрезков (или углов) от данных отрезков (или углов), только формула эта содержит кроме отрезков тригонометрические функции углов.[2]
Способ №13 (тригонометрический).
1. Из подобия ΔBOC и AOD: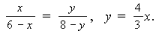 
Δ
2. ΔBOC – прямоугольный.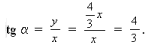 
3. Найдем cos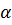
либо по формуле 
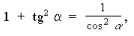либо методом треугольника: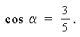
4. Из ΔBOC: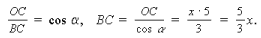 
5. Из ΔAOD: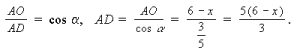
6. Средняя линия равна: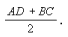
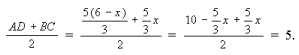
Ответ: 5 см.
Способ№ 14 (тригонометрический). 1. Из подобия треугольников BOC и AOD: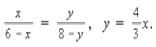 
2.
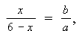,ax = 6b – bx, (a + b)x = 6b,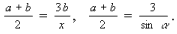 
3. 
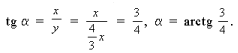
4.
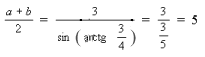
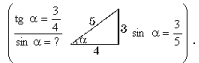Ответ: 5 см.
Метод площадей состоит в том, что главным объектом данного метода является площадь. Для треугольника площадь довольно просто выражается через разнообразные комбинации элементов треугольника.
Поэтому эффективным оказывается прием, когда сравниваются различные выражения для площади данной фигуры. В этом случае возникает уравнение, содержащее известные и искомые элементы фигуры, разрешая которое можно определить неизвестное. Особенность метода площадей в том, что из геометрической задачи он «делает» алгебраическую, сводя все к решению уравнения.[2]
Способ №15
1.
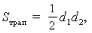так как диагонали d1 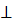d2.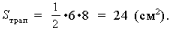 
2. 
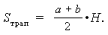
H – высота не только трапеции, но и прямоугольного треугольника с катетами 6 см и 8 см, проведенная из вершины прямого угла на гипотенузу. Находим
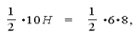
H=4,8
3. 
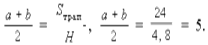Ответ: 5 см.
Метод координат
Координаты на плоскости можно вводить бесконечным числом разных способов. И, решая ту или иную геометрическую задачу методом координат, можно использовать различные координатные системы, выбирая ту из них, в которой задача решается проще, удобнее. [3]
1.Зададим оси координат по прямым BD и AC, точка О(0;0) – точка пересечения диагоналей.
2.Координаты вершин: А(0;у-8), В(х-6;0), С(0;у), D(х;0).
3.Найдем координаты точек М и N:
M (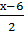
;
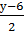), N (
;
), 
,
=
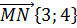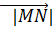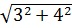=5. Ответ:5см.
Заключение
В ходе моей работы было выявлено 16 различных способов и 7 методов решения одной конкретной задачи из раздела «планиметрия». На примере этой задачи можно увидеть многообразие геометрической теории. Самым понятным и простым является метод, в котором используются дополнительные построения и метод координат. Самым трудным - метод введения вспомогательного неизвестного и методы, использующие соотношение между углами и сторонами треугольника. Здесь нужно производить сложные вычисления и трудно додуматься до такого решения. Ведь метод замены широко применяется в алгебре, но не менее эффективно «замена» может быть применена в геометрии. Отыскание различных способов решения задач – важнейшее средство развития творческого мышления. Решение одной и той же задачи различными способами дает возможность полнее исследовать свойства геометрической фигуры и выявить наиболее простые решения. Решая задачу подходящим методом, иногда попутно удается открыть новые свойства фигуры, о которых в задание ничего не говорится. Нередко найденный способ решения в дальнейшем используется при решении более трудных задач. Более того, отыскивая различные способы решения математической задачи, ученик развивает свои творческие возможности, формирует познавательный интерес, вырабатывает исследовательские навыки, применяя глубокие математические знания. Решение задач различными способами способствуют повышению математической культуры учеников!
Все перечисленное создает условия для формирования навыков исследовательской деятельности, способствующей накоплению творческого потенциала. Эти слова могу отнести к себе.
Выводы
Проведенное исследование позволило сделать следующие выводы:
1. Основным методом решения геометрических задач в условиях экзамена является аналитический метод. Тем не менее, важно, владеть геометрическими приемами, уметь находить наиболее простое и красивое решение с помощью дополнительных построений.
2. При решении задач чаще всего применяется комбинированный метод.
3. Можно овладеть основными методами решения задач, составляющих важную часть многих эвристических алгоритмов, учиться рационально, планировать поиск решения задачи, выполнять полезные преобразования условия задачи.
Библиографическая ссылка
Фролов Г.Р. ПЛАНИМЕТРИЯ В ОДНОЙ ЗАДАЧЕ // Международный школьный научный вестник. – 2020. – № 3. ;URL: https://school-herald.ru/ru/article/view?id=1352 (дата обращения: 19.04.2024).