Изучение многих физических процессов и геометрических закономерностей часто приводит к решению задач с параметрами («параметр» с греч. parametron–отмеривающий). В обыденной жизни мы употребляем слово «параметр» как величину, характеризующую какое-либо основное свойство процесса, явления или системы, машины, прибора (напряжение, электрическое сопротивление, масса, коэффициент трения и др.).
В математике параметр –это постоянная величина, выраженная буквой, сохраняющая свое постоянное значение лишь в условиях данной задачи.При математическом моделировании различных процессов часто возникают задачи с параметрами (уравнения или неравенства, системы уравнений и неравенств, построение семейства кривых). В курсе элементарной математики уравнения и неравенства с параметрами являются, пожалуй, самыми сложными задачами. Обычно мы встречаем линейные уравнения с параметром, и только иногда квадратные уравнения с тем же параметром. Поэтому у меня возникло желание разобраться в этой теме: уравнения второй степени с параметрами, дополнив её уравнениями, сводимыми к выше названным.
Данная тема актуальна, потому что нам может пригодится умение решать уравнения второй степени с параметрами при сдаче экзамена ЕГЭ по математике и при поступлении в высшие учебные заведения.
Гипотеза работы: количество корней и их значение будет зависеть от значения параметра.
Цель работы: систематизировать знания о решении уравнений второй степени с параметром, к ним сводимых уравнений и составить алгоритм их решения.
Для достижения поставленной цели необходимо решить следующие задачи:
1) дать определение понятию «уравнение с параметром»;
2) показать принцип решения уравнений второй степени с параметром на общих случаях;
3) показать решение уравнений второй степени с параметрами, используя аналитический метод;
4) составить алгоритм решения уравнений с параметрами.
Для выполнения поставленной цели были использованы следующие методы: использование литературы (учебных пособий по математике), и работа на занятиях по математике.
Объектом исследовательской работы было решение уравнений второй степени с параметрами.
1. Теоретические основы решения уравнений второй степени с параметром
Если в выражении с двумя неизвестными x и a,переменной a придавать какое-либо фиксированное значение, то это уравнение (или неравенство) можно рассматривать как задачу с одной переменной x. Множеством решения такой задачи является множество пар чисел x и a, при подстановке которых в исходное выражение получается верное равенство (или верное неравенство). Аргументы x и a считаются неравноправными, так как при решении задач обычно стараются найти x, выраженное через a. Далее необходимо выяснить зависимость решений от значений параметра a, что является важной частью решения задачи. Иногда ее называют исследованием и отделяют от непосредственного решения. Решить уравнение с параметром а – это значит для каждого значения а найти значения х, удовлетворяющие этому уравнению.
В квадратных уравнениях вида ax2+bx+c=0, где x – переменная, параметр является коэффициентом или частью коэффициента.
Задачи с параметрами можно разделить на два больших класса: задачи, в которых необходимо при всех значениях параметра из некоторого множества решить уравнение; задачи, в которых требуется найти все значения параметра, при каждом из которых решение уравнения удовлетворяют некоторым условиям. В итоге мы получаем алгоритм решения уравнений второй степени с параметром [1]:
Привести уравнение второй степени к виду 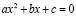 , где a, b и c– коэффициенты, x – переменная.
, где a, b и c– коэффициенты, x – переменная.
Определить область допустимых значений параметра и переменной.
Обратить внимание на коэффициент а, если здесь находится параметр, то следует рассмотреть случай, где a=0: уравнение вида ax2+bx+c=0, станет уравнением вида bx+c=0.
Найти дискриминант: D = b2–4ac (или 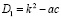 , где
, где 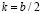 ). Он будет выражен через параметр. Как известно, от знака дискриминанта будет зависеть количество корней:
). Он будет выражен через параметр. Как известно, от знака дискриминанта будет зависеть количество корней:
Если D (D1)>0, то уравнение имеет два корня
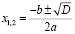 ,
, 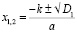 .
.
Если D (D1) = 0, то уравнение имеет один корень
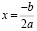 ,
, 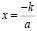 .
.
Если D (D1)< 0, то уравнение не имеет корней
Найденные контрольные значения параметра разбивают область допустимых значений параметра на промежутки. На каждом из промежутков нужно определить знак дискриминанта и посчитать значения переменной.
2. Основные методы решения уравнений второй степени, содержащих параметр
2.1. Неполные квадратные уравнения с параметром
Квадратное уравнение ах2+bх+с=0, где а ≠ 0 называется неполным, если хотя бы один из коэффициентов b или c равен 0.
Общая схема решения неполных квадратных уравнений с параметрами:
ах2=0, где а≠ 0, b=0, с=0. Если а≠0, то уравнение примет вид х2=0, х=0.
Следовательно, уравнение имеет два совпадающих корня, равных нулю.
Если а=0, то х – любое действительное число.
ах2+с=0, где а≠0, b=0, с≠0. Если а≠0, то уравнение примет вид:
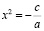 .
.
Если
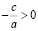 ,
, 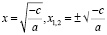 ,
,
следовательно, уравнение имеет корни, они равны по абсолютной величине, но противоположны по знаку. Если 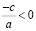 , то
, то 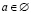 , следовательно, уравнение корней не имеет. Если а=0 и с≠0, то уравнение действительных корней не имеет.
, следовательно, уравнение корней не имеет. Если а=0 и с≠0, то уравнение действительных корней не имеет.
ах2+bх=0, где а≠0, b≠0, с=0. Если a≠0, то уравнение примет вид:
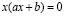 ,
, 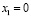 и
и 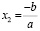 .
.
Если a=0, то bх=0, х=0.
Рассмотрим это на примере х2–2а+1=а, x – переменная, a – параметр.
x2–2a+1– a=0;
x2–3a+1=0.
Коэффициенты: a=1, b=0, c= –3a+1
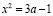 ,
,
если 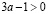 ,
, 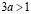 ,
, 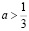 , то
, то
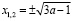 .
.
если 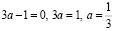 , то x=0.
, то x=0.
если 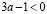 ,
, 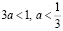 , то нет корней –
, то нет корней – 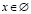 .
.
Ответ: при 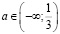 нет корней; при
нет корней; при 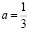 x=0; при
x=0; при
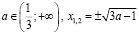 .
.
2.2. Приведённые квадратные уравнения с параметром
Приведённое квадратное уравнение – это уравнение вида ах2+bх+с=0, где a=1.
При решении приведённых квадратных уравнений с параметром нужно:
Рассмотреть случай, где параметр равен нулю.
Найти дискриминант: D = b2–4ac.
Если D>0, то уравнение имеет два корня
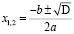 .
.
Если D=0, то уравнение имеет один корень
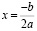 .
.
Если D<0, то уравнение не имеет корней
Решим уравнение 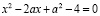 , x – переменная, a – параметр.
, x – переменная, a – параметр.
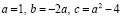
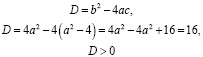
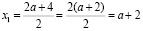 ;
;
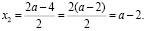
если a=0, то 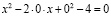 ;
;
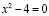 ;
;
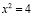 ;
;
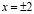 ;
;
Ответ: при любом а, 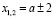
Решим уравнение 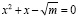 , x – переменная, m – параметр.
, x – переменная, m – параметр.
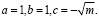
О.Д.З.: 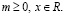
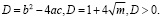
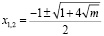 ,
,
если m=0, то 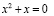
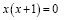
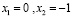
Ответ: если 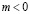 , то нет корней; если
, то нет корней; если 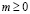 , то
, то 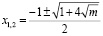 .
.
2.3. Уравнения второй степени с параметром
При решении уравнений второй степени будем пользоваться планом, предоставленным в теоретическом разделе.
Решим уравнение
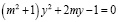 ,
,
где y – переменная, m – параметр.
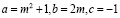 .
.
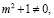 при любом m.
при любом m.
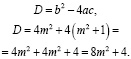
При любом m, D>0
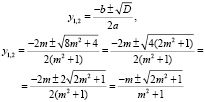
Ответ: при любом m,
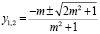 .
.
2.4. Уравнения второй степени с параметром с дополнительными условиями
Дополнительные условия могут формулироваться так:
При каком значении параметра уравнение имеет один/ два/ и более корня (не имеет корней)?
При каком значении параметра один (оба корня) равны нулю?
При каком значении параметра корни равны по модулю, но противоположны по знаку?
При каком значении параметра уравнения имеют хотя бы один общий корень и пр.?
При решении таких уравнений используются известные формулы для корней квадратного уравнения, теорема Виета и условия существования действительных решений – знак дискриминанта.
Решим уравнение
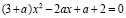 ,
,
где х – переменная, а – параметр.
При каких значениях параметра a уравнение:
a) имеет два различных действительных корня;
b) имеет один корень;
c) не имеет действительных корней;
d) имеет один из корней равный нулю;
e) имеет оба корня равных нулю;
f) имеет корни равные по модулю, но противоположные по знаку?
Решение:
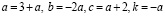
если 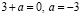 , то
, то
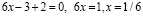 ;
;
если 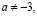 то
то
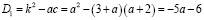
если 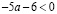 ,
, 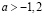 , то нет корней
, то нет корней
если 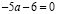 ,
, 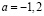 , то
, то 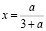
если 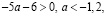 то
то
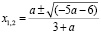
если a=0, то 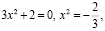 нет корней
нет корней
a) 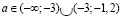 ;
;
b) 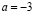 и
и 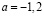 ;
;
c) 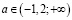 ;
;
d) Уравнение должно иметь вид
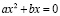 , где a≠0, b≠0.
, где a≠0, b≠0.
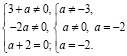
e) Уравнение должно иметь вид
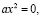 где
где 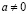
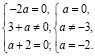
Система не имеет решений.
Таких значений параметра нет.
f) Уравнение должно иметь вид
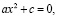 где
где 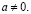
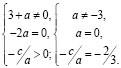
Таких значений параметра нет.
Ответ:
a) 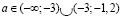
b) 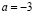 и
и 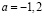
c) 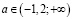
d) 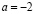
e) Таких значений параметра нет.
f) Таких значений параметра нет.
Применение теоремы виета
Теорема Виета гласит: для того чтобы числа x1 и x2 были корнями уравнения 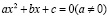 , необходимо и достаточно выполнения равенств:
, необходимо и достаточно выполнения равенств:
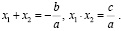
Решим уравнение, используя теорему Виета.
При каком a уравнение
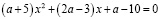
имеет два различных отрицательных корня?
Решение:
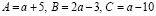
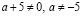
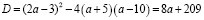
Оба корня будут отрицательными, если
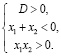
Тогда
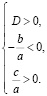
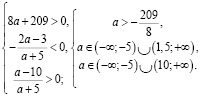
Ответ: 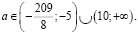
2.5. Дробно-рациональные уравнения с параметром, сводимые к уравнениям второй степени
Когда мы решаем дробно-рациональное уравнение, первым делом нужно его преобразовать. Если полученное уравнение является уравнением второй степени с параметром, исследуем его и решаем уравнение с параметром, учитывая область допустимых значений.
Решим уравнение
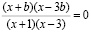
О.Д.З.: 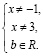
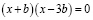
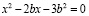
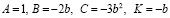
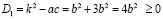
если 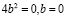 , то
, то 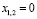
если 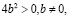 то
то 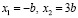
если 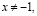 то
то
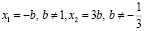
если 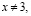 то
то
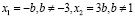
если 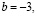 то
то 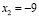 если
если 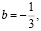 то
то 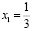 .
.
Ответ: если 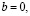 то
то 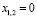 .
.
если 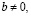 то
то 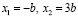
если
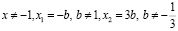
если 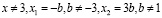
если 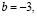 то
то 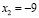
если 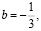 то
то 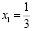
2.6. Более сложные уравнения второй степени с параметром
Решим задачу: сколько корней в зависимости от параметра а имеет уравнение
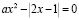 ?
?
Решение:
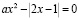 ,
,
О.Д.З.: 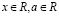
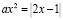 , если
, если 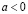 , то корней нет
, то корней нет
если a=0, то
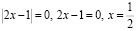 – один корень
– один корень
если 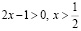 , то
, то
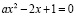
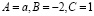 ,
, 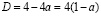
если 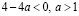 , то нет корней
, то нет корней
если 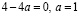 , то
, то
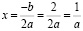 – один корень
– один корень
если 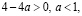 то
то
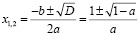 – два корня
– два корня
если 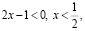 то
то
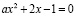
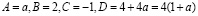
если 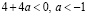 , то нет корней
, то нет корней
если 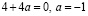 , то
, то
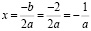 – один корень
– один корень
если 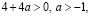 то
то
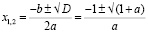 – два корня
– два корня
Получившийся результат соберём на одной числовой оси. Это и будет ответ.
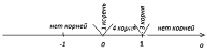
Ось ответа
Заключение
В ходе исследовательской работы я собрала и обобщила весь материал по теме: «Решение уравнений второй степени с параметром». Кроме того, я углубила свои знания. Как уже говорилось ранее, решить уравнение с параметром а – это значит, для каждого значения а найти значения х, удовлетворяющие этому уравнению. Моя гипотеза о том, что количество корней и их значение будут зависеть от значений параметра, подтвердилась.
Были показаны общие случаи решения уравнений второй степени с параметром, а именно решение неполных, приведённых и других квадратных уравнений с параметром, были рассмотрены уравнения второй степени с параметром с дополнительными условиями и более сложные уравнения. Теория сопровождалась практическими примерами решения уравнений второй степени с параметром.
Был составлен алгоритм решения уравнений второй степени с параметром (см. Раздел 1: Теоретические основы решения уравнений второй степени с параметром):
Привести уравнение второй степени к виду 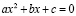 , где a, b и c– коэффициенты, x – переменная.
, где a, b и c– коэффициенты, x – переменная.
Определить область допустимых значений параметра и переменной.
Обратить внимание на коэффициент а, если здесь находится параметр, то следует рассмотреть случай, где a=0: уравнение вида ax2+bx+c=0, станет уравнением вида bx+c=0.
Найти дискриминант: D=b2–4ac (или 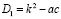 , где
, где 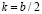 ). Он будет выражен через параметр. Как известно, от знака дискриминанта будет зависеть количество корней:
). Он будет выражен через параметр. Как известно, от знака дискриминанта будет зависеть количество корней:
Если D (D1) >0, то уравнение имеет два корня
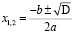 ,
, 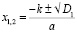 .
.
Если D (D1) = 0, то уравнение имеет один корень
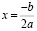 ,
, 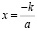 .
.
Если D (D1)<0, то уравнение не имеет корней.
Найденные контрольные значения параметра разбивают область допустимых значений параметра на промежутки. На каждом из промежутков нужно определить знак дискриминанта и посчитать значения переменной.
Библиографическая ссылка
Дьяченко Н.Е. УРАВНЕНИЯ ВТОРОЙ СТЕПЕНИ С ПАРАМЕТРОМ И К НИМ СВОДИМЫЕ // Международный школьный научный вестник. 2019. № 2-4. ;URL: https://school-herald.ru/ru/article/view?id=1029 (дата обращения: 19.01.2026).
