Международный школьный научный вестник

Научный журнал для старшеклассников и учителей ISSN 2542-0372

• Авторы
• Научный руководитель
• Файлы
• Литература

Сырых М. 1

---

1 г. Ногинск Московской области, МБОУ «СОШ № 21», 11 класс

Туманов В.Е. (Ногинск Московской области, МБОУ «СОШ № 21»)

Статья в формате PDF

0 KB

1. Семенов Н.Н. О некоторых проблемах химической кинетики и реакционной способности. Изд-во АН СССР. – М., 1958. – 686 с.

2. Денисов Е.Т. Новые эмпирические модели реакций радикального отрыва // Успехи химии. – 1997. – Т. 66; № 10. – С. 953–971.

3. Денисов Е.Т., Туманов В.Е. Модель переходного состояния как результат пересечения двух термов Морзе в приложении к реакциям атомарного водорода // Журнал физической химии. – 1994. – Т. 68; № 4. – С. 719–725.

4. Маккалох Дж., Питтс У. Логические исчисления идей, относящихся к нервной деятельности // Автоматы. – М.: ИЛ, 1956. (McCulloch W., Pitts W. A Logical Calculus of the Ideas Immanent in Nervous Activity // Bulletin of Mathematical Biophysics. 1943. Vol 5. pp. 115–133.)

5. Bryson A.E., Ho Y.-C. Applied optimal control: optimization, estimation,and control / Blaisdell Publishing Company or Xerox College Publishing, 1969. – pp. 481.

6. Rumelhart D.E., Hinton G.E., Williams R.J. Learning internal representations by error propagation / In D.E. Rumelhart, J.L. McClelland editors // Parallel Distributed Processing: Explorations in the Microstructure of Cognition. Vol. 1: Foundations Vol. 1: Foundations, MIT Press, Cambridge, MA.

7. Алгебра и начала анализа: учеб. для 11 кл. общеобразоват. учреждений / С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин. – М.: Просвещение, 2002. – 448 с.

8. Колмогоров А.Н. О представлении непрерывных функций нескольких переменных в виде суперпозиции непрерывных функций одного переменного // Доклады АН СССР. – 1958. – Т. 114, № 5. – С. 953–956.

9. Cybenko G.V. Approximation by Superpositions of a Sigmoidal function // Mathematics of Control Signals and Systems. – 1989. – Vol. 2; №. 4. – PP. 303–314.

10. Туманов В.Е. От проблемно-ориентированных баз данных к извлечению новых знаний в химической кинетике и термохимии радикальных жидкофазных реакций (Литературный обзор) // Научное обозрение. – 2016. – № 2. – С. 81–92.

11. Tumanov V.E. Hybrid algorithm of application of artificial neuronets for an evaluation of rate constants of radical bimolecular reactions // Advances in Neural Networks, Fuzzy Systems and Artificial Intelligence. Recent Advances in Computer Engineering Series. Jerzy Balicski (Eds) WSEAS Press. Gdansk, Poland, 15–17 may 2014. – Vol. 21. – PP. 58–61.

12. Заенцев И. В. Нейронные сети: основные модели: учебное пособие. – Воронеж: ВГУ, 1999. – 78 с.

13. Туманов В.Е., Денисов Е.Т. Оценка энергии диссоциации S-H и C-H-связей в серосодержащих соединениях // Нефтехимия. – 2003. – Т. 43; № 6. – C. 406–411.

14. Денисов Е.Т., Туманов В.Е. Оценка энергий диссоциации связей по кинетическим данным радикальных жидкофазных реакций // Успехи химии. – 2005. – Т. 74; № 9. – С. 905–938.

15. Luo Y.-R., Comprehensive Handbook of Chemical Bond Energies. – London – New York: CRC Press, Boca Raton, 2007. – 1655 p.

В последнее время возникло новое направление научных исследований – анализ научных данных с применением методов искусственного интеллекта (Data Science) . Математическое моделирование и анализ накопленных экспериментальных данных о протекании химических процессов с использованием информационных технологий является составной частью любого современного научно-прикладного исследования в области изучения элементарных химических реакций. Одной из характеристик химической реакции являются ее скорость или энергия активации (реакционной способности) , в частности, константа скорости, знание которой позволяет предсказывать ход химической реакции, моделировать химические процессы в пищевой и фармацевтической промышленности. Поэтому предсказание реакционной способности различных типов элементарных химических реакций является важной научно-практической задачей.

Актуальность, научная новизна и практическая ценность. Массив экспериментальных данных по реакционной способности (энергии активации или классического потенциального барьера) органических соединений в радикальных реакциях отрыва атома водорода от тиолов и тиофенолов является небольшим, а эти соединения активно используются в органическом синтезе, в медицине, в фармакологии. Теоретические расчеты сложны и занимают много машинного времени (от 3 месяцев и больше) . Поэтому предсказание реакционной способности этих соединений в указанных выше химических реакциях по экспериментальным данным является актуальной научно-практической задачей.

Цель настоящего исследования – разработать и апробировать искусственную нейронную сеть для предсказания классического потенциального барьера радикальной реакции отрыва атома водорода от тиолов и тиофенолов по экспериментальным данным.

Задачами исследования являются:

1. Собрать экспериментальный материал и представить его в цифровом виде;

2. Разработать программу для моделирования искусственной нейронной сети для решения поставленной задачи на языке программирования Паскаль;

3. Обучить искусственную нейронную сеть предсказывать классический потенциальный барьер радикальных реакций отрыва атома водорода от тиолов и тиофенолов (компьютерный эксперимент) .

Гипотеза исследования. Из анализа литературных источников следует (см. обзор литературы):

1) разработаны эмпирические модели предсказания реакционной способности органических соединений в радикальных реакций отрыва;

2) технология искусственных нейронных сетей была успешно применена для решения задачи предсказания реакционной способности для некоторых классов органических соединений в таких реакциях. Поэтому поставленная цель может быть достигнута путем компьютерного эксперимента.

Предметом исследования является моделирование с помощью искусственной нейронной сети зависимости классического потенциального барьера от классической энтальпии и кинетического параметра радикальных реакций отрыва атома водорода от тиолов и тиофенолов по экспериментальным данным.

Обзор литературы

Определения используемых терминов приведены в Приложении 1.

Краткая история вопроса касается трех основных моментов: эмпирические модели радикальных реакций, искусственные нейронные сети и аппроксимация функций многих переменных.

Начало исследований по предсказанию энергии активации радикальных реакций по эмпирическим данным было положено известным линейным соотношением Поляни-Семенова [1] (Семенов Н.Н., академик АН СССР, лауреат Нобелевской премии по химии, один из основателей научной дисциплины «Химическая физика») и в дальнейшем получило свое развитие в работах [2, 3] и ряда других: корреляционные уравнения в рамках модели пересекающихся парабол и пересекающих термов Морзе.

Искусственная нейронная сеть была предложена в 1943 году Урнером Мак-Каллоком и Уолтером Питтсом как пороговое устройство с несколькими входами и одним (бинарным) выходом [4]. Сами авторы исследования рассматривали искусственный нейрон, как математическую модель решателя задач.

В 1969 году М. Минский и С. Пейперт доказали, что однослойные искусственные нейронные сети не могут решать определенные классы практических задач. Поэтому к ним на несколько лет был потерян интерес.

Однако к середине 80-х годов прошлого века математики нашли способы эффективного обучения многослойных искусственных нейронных сетей, которые стали активно использоваться в различных областях человеческого знания для решения задач [5, 6]: классификации, аппроксимации, оптимизации, кластеризации.

С задачей аппроксимации функций мы начинаем сталкиваться со школьной скамьи. На элективном курсе по алгебре и математическому анализу мы знакомимся с теоремой Лагранжа (f(x) – f(x0) =f'(c) x) и далее с формулой Тейлора – разложением в ряд в окрестности заданной абсциссы дифференцируемой функции. Мы начинаем понимать, что такую функцию можно представить в виде суммы степенных функций с достаточной степенью точности [7].

В 1956 году академик Колмогоров А.Н. доказывает теорему о том, что любая непрерывная функция многих переменных может быть представлена (аппроксимирована) через функции одной переменной [8]. Эта теорема является математическим фундаментом искусственных нейронных сетей при аппроксимации функций.

Основываясь на этой теореме в 1989 году Джордж Цыбенко доказал универсальную теорему аппроксимации о том [9], что нейронная сеть прямого распространения с одним скрытым слоем может аппроксимировать любую непрерывную функцию многих переменных с любой точностью.

В обзоре [10] представлены различные подходы применения искусственных нейронных сетей к оценке реакционной способности молекул в химических реакциях по экспериментальным данным (в контексте поставленной в настоящем исследовании проблемы).

Алгоритм, который положен нами в основу создания искусственной нейронной сети для предсказания классического потенциального барьера радикальной реакции отрыва атома водорода от тиолов и тиофенолов описан в [11].

Разработанная искусственная нейронная сеть позволяет с достаточной степенью предсказывать классический потенциальный барьер указанных выше реакций по экспериментальным данным, что делает результаты настоящей работы актуальными и практически ценными для определенного круга специалистов химиков.

Методы исследования. В работе использовался метод исследования, который состоял в описании (отбор и представление) экспериментальных данных по константам скорости радикальных реакций отрыва атома водорода от тиолов и тиофенолов, взятых из литературных источников.

Для реализации была выбрана искусственная нейронная сеть прямого распространения [12], состоящая из двух входных нейронов, семи нейронов скрытого слоя и одного выходного нейрона.

В качестве языка программирования был выбран Pascal ABC.

Основная часть

По константе скорости и температуре протекания реакции вычислялись экспериментальная энергий активации, классический потенциальный барьер, классическая энтальпия реакции, кинетический параметр. При этом кинетический параметр вычислялся по уравнениям модели пересекающихся парабол [2].

Экспериментальные данные по константам скорости радикальных реакций отрыва атома водорода от тиолов и тиофенолов были взяты из коллекции, представленной в работе [13] и включали 23 реакции, 6 из которых представляли контрольную выборку. Фрагмент данных приведен в табл. 1.

Таблица 1

Фрагмент данных, Т – температура, градусы К, k – константа скорости, л моль-1 с-1, DР – энергия разрываемой связи, кДж/моль, DO – энергия образующейся связи, кДж/моль, bre – кинетический параметр, (кДж/моль) 1/2

Энергии диссоциации связей для вычисления классической энтальпии реакции были взяты из обзора [14] и справочника [15].

Топологическая структура сети приведена на рисунке.

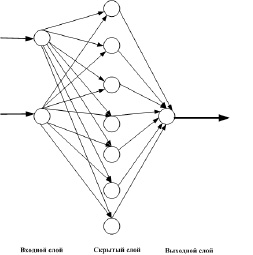
Топология искусственной нейронной сети

Активационная функция имеет вид:

.

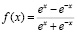Искусственная нейронная сеть была обучена за 500 итераций с использованием правила Хебба [12]. Ошибка обучения составляет 0,11 кДж/моль.

Алгоритм реализации и обучения сети имеет вид:

Const numInputs = 3; // число входов

numPatterns = 23; // число шаблонов

numHidden = 7; // число скрытых слоев

numEpochs = 500; // число итераций при обучении, ограничено

LR_IH = 0.7;

LR_HO = 0.07;

Var patNum:integer;

errThisPat:double; // Ошибка выхода сети

outPred:double; // Предыдущее значение выхода сети

RMSerror:double; // Общая ошибка сети

hiddenVal: array [1..numHidden] of double; // выходы скрытых слоев

wiegthsIH: array [1..numInputs, 1..numHidden] of double; // веса скрытых слоев

wiegthsHO: array [1..numHidden] of double; // веса на выходе

trainInputs: array [1..numPatterns, 1..numInputs] of double; // данные

trainOutput: array [1..numPatterns] of double; // выходы

patNum:=0;

outPred:=0.0;

errThisPat:=0.0;

RMError:=0.0;

initWeigths; // Начальные значения весов

initData; // Загрузить данные

// Обучаем сеть

for j:=1 to numEpochs do

begin

for i:=1 to numPaterm do

begin

// выбираем шаблон

patNum:=SelPatten;

// вычислить текущий выход сети и ошибку для выбранного шаблона

calcNet;

// изменить веса

weigthChangesHO;

weigthChangesIH;

end;

// показывать общую ошибку сети после каждого для каждой итерации

calcOverallError;

end;

// Показать результат обучения

diplayResults;

end.

Таблица 2

Результаты обучения искусственной нейронной сети. Значения приведены в относительных единицах (масштабированы на максимальные значения переменных)

Результаты и обсуждение

Как видно из табл. 2, искусственная нейронная сеть предсказывает значение классического барьера радикальных реакций (энергии активации реакции) тиолов и тиофенолов с приемлемой точностью. Среднеквадратичная ошибка по всей выборке составляет 0.06±0.20 кДж/моль, находится в хорошем согласии с погрешностью экспериментальными методами определения энергии активации для таких реакций ±4 кДж/моль.

Таким образом, разработанная программа может быть использована для предсказания классического потенциального барьера радикальных реакций тиолов и тиофенолов в жидкой фазе для соединений с известными экспериментальными параметрами.

Выводы

Разработана программная реализация искусственной нейронной сети для аппроксимации функций двух переменных на языке программирования Pascal ABC.

Обучена искусственная нейронная сеть, аппроксимирующая зависимость классического потенциального барьера радикальных реакций отрыва атома водорода от тиолов и тиолофенолов в жидкой фазе от экспериментальных термохимических данных.

Приложение 1

Определения используемых терминов

Константа скорости (kexp) вычисляется по формуле Аррениуса

,

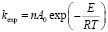где A0 – предэспоненциальный множитель на одну эквиреакционную связь; n – число эквиреакционных связей в молекуле; Е – экспериментальная энергия активации.

Модель пересекающихся парабол для реакций радикального отрыва.

Радикальная реакция отрыва атома водорода

R•-·+ R1H→ RH +R•1-

в этой модели характеризуется следующими величинами.

Классической энтальпией реакции

DHe = Di – Df + 0,5 (hLνi – hLνf),

которая представляет собой изменение потенциальной энергии системы, если ее измерять между точками минимума потенциальных кривых реагирующих связей с учетом нулевых энергий колебания соответствующих связей. νi – частота колебания молекулы вдоль разрываемой связи, νf – частота колебания молекулы вдоль образующейся связи, h – постоянная Планка, L – число Авогадро, Di – энергия диссоциации разрываемой связи, Df – энергия диссоциации образующейся связи.

Классическим потенциальным барьером

Eei = Ei + 0,5 (hLcνi – RT),

которая отсчитывается от минимума потенциальной кривой рвущейся связи до точки минимума переходного состояния. Ei – экспериментальная энергия активации, R – газовая постоянная, T – абсолютная температура в °К, Ei – экспериментальная энергия активации радикальной реакции.

Расстоянием re, между вершинами потенциальных кривых в координатах: амплитуда валентного колебания атомов – потенциальная энергия.

Коэффициентами

b = p(2µi)1/2νi и bf = p(2µf) 1/2νf,

которые описывают зависимость потенциальной энергии от амплитуды колебаний атомов вдоль рвущейся (i) и образующейся (f) валентной связи. 2b2 – силовая постоянная связи, µi – приведенная масса атомов для разрываемой связи, µf – приведенная масса атомов для образующейся связи.

Указанные характеристики в параболической модели связаны соотношением (кинетический параметр)

,

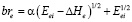где a = b/bf .

Свободный радикал (монорадикал) – многоатомная нейтральная (не имеющая заряда) частица, обладающая неспаренным электроном. Свободный радикал – парамагнитная частица. Как правило, свободные радикалы быстро вступают друг с другом в реакции рекомбинации и диспропорционирования. Многие свободные радикалы обладают высокой реакционной способностью в реакциях с молекулами.

Энергия диссоциации индивудуальной связи в молекуле – энергия, необходимая для гомолитического разрыва данной связи. Например, в пропане энергия разрыва С-Н -связи в метильной группе составляет 422 кДж моль-1, а в метиленовой группе 412 кДж моль-1. Средняя энергия разрыва всех однотипных связей в молекуле равна среднеарифметическому всех энергий диссоциации индивидуальных связей. Например, в метане ЭДС связи СН3−Н равна 440 кДж моль-1, а среднее значение всех 4 С− Н связей равно всего 200 кДж моль-1.

Соотношение Поляни-Семенова. Линейное эмпирическое соотношение между энергией активации радикальной реакции Е и энтальпией реакции ∆Н.

Тиолы – органические соединения, включающие атом серы в конце углеводородной цепи, например, CH3–CH2–SH.

Тиофенолы – органические соединения, включающие атом серы за фенильным кольцом, например, PhSH.

Приложение 2

Листинг программы

program MLP_Pascal;

Const numInputs = 3; // число входов

numPatterns = 23; // число шаблонов

numHidden = 7; // число скрытых слоев

numEpochs = 500; // число итераций при обучении, ограничено

LR_IH = 0.7;

LR_HO = 0.07;

Var patNum:integer;

errThisPat:double; // Ошибка выхода сети

outPred:double; // Предыдущее значение выхода сети

RMSerror:double; // Общая ошибка сети

hiddenVal: array [1..numHidden] of double; // выходы скрытых слоев

wiegthsIH: array [1..numInputs, 1..numHidden] of double; // веса скрытых слоев

wiegthsHO: array [1..numHidden] of double; // веса на выходе

trainInputs: array [1..numPatterns, 1..numInputs] of double; // данные

trainOutput: array [1..numPatterns] of double; // выходы

j,i:integer;

// инициализация значений весов (подобраны)

Procedure initWeigths() ;

Var j,i:integer;

begin

for j:=1 to numHidden do

begin

wiegthsHO[j]:=1.0;

for i:=1 to numInputs do wiegthsIH[i,j]:=0.8;

end;

end;

// шаблоны обучения

Procedure initData() ;

var bremi,brema,E_max,E_min,dH_min,dH_max:double;

begin

// кинетический параметр

bremi:= 13.0;

brema:= 18.0;

// классический потенциальный барьер

E_max := 58.0;

E_min := 33.0;

// энтальпия

dH_min := -292.0;

dH_max := 18.0;

trainInputs[1,1]:=(-44.31 – dH_min) / (dH_max – dH_min) ;

trainInputs[1,2]:= (16.56- bremi) / (brema – bremi) ;

trainInputs[1,3]:=1.0; // смещение

trainOutput[1]:= (54.89 – E_min) / (E_max – E_min) ;

trainInputs[2,1]:=(-45.81 – dH_min) / (dH_max – dH_min) ;

trainInputs[2,2]:= (16.56 - bremi) / (brema – bremi) ;

trainInputs[2,3]:=1.0;

trainOutput[2]:= (54.33 – E_min) / (E_max – E_min) ;

trainInputs[3,1]:=(-0.71- dH_min) / (dH_max – dH_min) ;

trainInputs[3,2]:= (13.96- bremi) / (brema – bremi) ;

trainInputs[3,3]:=1.0;

trainOutput[3]:= (52.65 – E_min) / (E_max – E_min) ;

trainInputs[4,1]:=(0.09- dH_min) / (dH_max – dH_min) ;

trainInputs[4,2]:= (14.00- bremi) / (brema – bremi) ;

trainInputs[4,3]:=1.0;

trainOutput[4]:= (53.63 – E_min) / (E_max – E_min) ;

trainInputs[5,1]:=(-38.51 - dH_min) / (dH_max – dH_min) ;

trainInputs[5,2]:= (15.66 – bremi) / (brema – bremi) ;

trainInputs[5,3]:=1.0;

trainOutput[5]:= (57.25 – E_min) / (E_max – E_min) ;

trainInputs[6,1]:=(1.49 - dH_min) / (dH_max – dH_min) ;

trainInputs[6,2]:= (12.05 – bremi) / (brema – bremi) ;

trainInputs[6,3]:=1.0;

trainOutput[6]:= (39.02 – E_min) / (E_max – E_min) ;

trainInputs[7,1]:=(2.69 - dH_min) / (dH_max – dH_min) ;

trainInputs[7,2]:= (14.00 – bremi) / (brema – bremi) ;

trainInputs[7,3]:=1.0;

trainOutput[7]:= (54.29 – E_min) / (E_max – E_min) ;

trainInputs[8,1]:=(1.79 - dH_min) / (dH_max – dH_min) ;

trainInputs[8,2]:= (13.20 - bremi) / (brema – bremi) ;

trainInputs[8,3]:=1.0;

trainOutput[8]:= (48.32 – E_min) / (E_max – E_min) ;

trainInputs[9,1]:=(-0.71 - dH_min) / (dH_max – dH_min) ;

trainInputs[9,2]:= (13.34 - bremi) / (brema – bremi) ;

trainInputs[9,3]:=1.0;

trainOutput[9]:= (48.05 – E_min) / (E_max – E_min) ;

trainInputs[10,1]:=(-48.51 - dH_min) / (dH_max – dH_min) ;

trainInputs[10,2]:= (14.84 - bremi) / (brema – bremi) ;

trainInputs[10,3]:=1.0;

trainOutput[10]:= (39.06 – E_min) / (E_max – E_min) ;

trainInputs[11,1]:=(-3.71 - dH_min) / (dH_max – dH_min) ;

trainInputs[11,2]:= (13.20 - bremi) / (brema – bremi) ;

trainInputs[11,3]:=1.0;

trainOutput[11]:= (47.76 – E_min) / (E_max – E_min) ;

trainInputs[12,1]:=(-3.71 - dH_min) / (dH_max – dH_min) ;

trainInputs[12,2]:= (13.20 - bremi) / (brema – bremi) ;

trainInputs[12,3]:=1.0;

trainOutput[12]:= (47.76 – E_min) / (E_max – E_min) ;

trainInputs[13,1]:=(-0.31- dH_min) / (dH_max – dH_min) ;

trainInputs[13,2]:= (14.00- bremi) / (brema – bremi) ;

trainInputs[13,3]:=1.0;

trainOutput[13]:= (52.79 – E_min) / (E_max – E_min) ;

trainInputs[14,1]:=(-30.61 - dH_min) / (dH_max – dH_min) ;

trainInputs[14,2]:= (15.84 - bremi) / (brema – bremi) ;

trainInputs[14,3]:=1.0;

trainOutput[14]:= (54.53 – E_min) / (E_max – E_min) ;

trainInputs[15,1]:=(-28.51 - dH_min) / (dH_max – dH_min) ;

trainInputs[15,2]:= (15.66- bremi) / (brema – bremi) ;

trainInputs[15,3]:=1.0;

trainOutput[15]:= (53.70 – E_min) / (E_max – E_min) ;

trainInputs[16,1]:=(-32.21 - dH_min) / (dH_max – dH_min) ;

trainInputs[16,2]:= (15.66- bremi) / (brema – bremi) ;

trainInputs[16,3]:=1.0;

trainOutput[16]:= (51.92 – E_min) / (E_max – E_min) ;

trainInputs[17,1]:=(-22.21- dH_min) / (dH_max – dH_min) ;

trainInputs[17,2]:= (15.40- bremi) / (brema – bremi) ;

trainInputs[17,3]:=1.0;

trainOutput[17]:= (53.76 – E_min) / (E_max – E_min) ;

trainInputs[18,1]:=(-26.51 – dH_min) / (dH_max – dH_min) ;

trainInputs[18,2]:= (15.10 – bremi) / (brema – bremi) ;

trainInputs[18,3]:=1.0;

trainOutput[18]:= (49.88 – E_min) / (E_max – E_min) ;

trainInputs[19,1]:=(0.09 – dH_min) / (dH_max – dH_min) ;

trainInputs[19,2]:= (13.20 – bremi) / (brema – bremi) ;

trainInputs[19,3]:=1.0;

trainOutput[19]:= (47.14 – E_min) / (E_max – E_min) ;

trainInputs[20,1]:=(-48.51 – dH_min) / (dH_max – dH_min) ;

trainInputs[20,2]:= (15.66 - bremi) / (brema – bremi) ;

trainInputs[20,3]:=1.0;

trainOutput[20]:= (55.32 – E_min) / (E_max – E_min) ;

trainInputs[21,1]:=(-0.21 - dH_min) / (dH_max – dH_min) ;

trainInputs[21,2]:= (13.20 - bremi) / (brema – bremi) ;

trainInputs[21,3]:=1.0;

trainOutput[21]:= (47.69 – E_min) / (E_max – E_min) ;

trainInputs[22,1]:=(0.19 - dH_min) / (dH_max – dH_min) ;

trainInputs[22,2]:= (10.13 - bremi) / (brema – bremi) ;

trainInputs[22,3]:=1.0;

trainOutput[22]:= (27.97– E_min) / (E_max – E_min) ;

trainInputs[23,1]:=(-31.31 - dH_min) / (dH_max – dH_min) ;

trainInputs[23,2]:= (15.66 - bremi) / (brema – bremi) ;

trainInputs[23,3]:=1.0;

trainOutput[23]:= (52.38– E_min) / (E_max – E_min) ;

end;

// Вычислить выход сети

Procedure calcNet() ;

var i,j:integer;

begin

// вычислить выходы скрытых нейронов, функция активации гиперболический тангенс

for i:=1 to numHidden do

begin

hiddenVal[i]:=0.0;

for j:=1 to numInputs do

hiddenVal[i]:=hiddenVal[i]+trainInputs[patNum,j]*wiegthsIH[j,i];

// hiddenVal[i]:=1.0/(1.0+exp( -1.0*hiddenVal[i]) ; ‘ функция активации сигмоида

hiddenVal[i]:=(exp( hiddenVal[i]) – exp( -1.0*hiddenVal[i]) ) /(exp( hiddenVal[i]) + exp( -1.0*hiddenVal[i]) ) ;

end;

// вычислить выход сети, функция активации линейная

outPred:=0.0;

for i:=1 to numHidden do

outPred:=outPred+hiddenVal[i]*wiegthsHO[i];

// вычислить ошибку

errThisPat:=outPred-trainOutput[patNum];

end;

// изменить веса скрытый нейрон – выход

procedure weigthChangesHO() ;

var k:integer;

wieghtChange:double;

begin

for k:=1 to numHidden do

begin

wieghtChange:=LR_HO*errThisPat*hiddenVal[k];

wiegthsHO[k]:= wiegthsHO[k]-wieghtChange;

if wiegthsHO[k] < – 4.5 then wiegthsHO[k]:=-4.5

else if wiegthsHO[k] >4.5 then wiegthsHO[k]:=4.5;

end;

end;

// изменить веса вход – скрытый нейрон

procedure weigthChangesIH() ;

Var i,k:integer;

x,wiegthChange,y:double;

begin

for i:=1 to numHidden do

for k:=1 to numInputs do

begin

x:=1.0 – hiddenVal[i]*hiddenVal[i];

x:=x*errThisPat*LR_IH;

y:=trainInputs[patNum,k];

x:=x*y;

wiegthChange:=x;

wiegthsIH[k,i]:=wiegthsIH[k,i] – wiegthChange;

end;

end;

// вычислить ошибку сети

procedure calcOverallError() ;

var i:integer;

begin

RMSerror:=0.0;

for i:=1 to numPatterns do

begin

patNum:=i;

calcNet() ;

RMSerror:=RMSerror+errThisPat*errThisPat;

end;

RMSerror:=RMSerror/numPatterns;

RMSerror:=sqrt(RMSerror) ;

end;

// Показать результаты

procedure diplayResults() ;

Var i:integer;

begin

for i:=1 to numPatterns do

begin

patNum:=i;

CalcNet() ;

writeln(‘Номер шаблона =’, patNum, ‘ Фактически’,trainOutput[patNum],’ Нейросеть =’, outPred) ;

end;

end;

Begin

patNum:=0;

outPred:=0.0;

errThisPat:=0.0;

RMSerror:=0.0;

initWeigths; // Начальные значения весов

initData; // Загрузить данные

// Обучаем сеть

for j:=1 to numEpochs do

begin

for i:=1 to numPatterns do

begin

// выбираем шаблон

patNum:=i;

// вычислить текущий выход сети и ошибку для выбранного шаблона

calcNet;

// изменить веса

weigthChangesHO;

weigthChangesIH;

end;

// показывать общую ошибку сети после каждого для каждой итерации

calcOverallError;

end;

// Показать результат обучения

diplayResults;

end.

Библиографическая ссылка