Международный школьный научный вестник

Научный журнал для старшеклассников и учителей ISSN 2542-0372

• Авторы
• Научный руководитель
• Файлы
• Литература

Жуков М.В. 1

---

1 п. Полевой, МОУ СОШ п. Полевой, 11 класс

Жуков В.Н. (п. Полевой, МОУ СОШ п. Полевой)

Статья в формате PDF

2835 KB

1. Ерёмин И.Е., канд. физ.-мат. Наук, М.С. Сычёв. Модифицированный алгоритм улучшения сходимости решёточных сумм. – Благовещенск: Амурский государственный университет, 2010. – 22 с.

2. Новиков Л.С., Воронина Е.Н. Перспективы применения наноматериалов в космической технике. Учебное пособие. – М: Университетская книга, 2008. – 188 с.

3. Павлов П.В., Хохлов А.Ф. Физика твёрдого тела. – М.: Высшая школа, 2000. – 494 с.

4. Розин К.М. Петраков В.С. Кристаллофизика: учебное пособие. – М.: Издательство МИСиС, 2006. – 249 с.

5. Шаскольская М.П. Кристаллография: Учеб. Пособие для втузов. – 2-е изд., перераб. и доп. – М.: Высш. Шк., 1984. – 376 с.

Настоящая научная работа посвящена описанию кристаллической решётки объёмноцентрированной структуры математической моделью, при помощи векторного метода компьютерного моделирования.

Считаем актуальным рассмотрение энергии наночастиц, т.к. предлагаемый метод может быть использован не только для определения энергии нанокрсталлов любого типа, но и в создании материалов с наноструктурой 0D, 1D, 2D, 3D.

Цели нашей работы:

1. Точное описание структуры кристалла математической моделью, путём прямого суммирования векторным методом;

2. Применить векторный метод компьютерного моделирования для получения 3D модели кристаллической решётки типа CsCl.

Гипотезы:

1. Возможно, для определения структурных сумм кристалла с малым числом частиц, подойдёт векторный метод компьютерного моделирования;

2. Предположим, что с помощью векторного метода компьютерного моделирования возможно определение квантово-размерных эффектов нанокристаллов.

3. Возможно, метод используемый в нашей работе, может быть применён при создании наноматериалов с запрограммированной структурой.

Задачи:

1. Сделать вывод формул структурных сумм для ОЦК на примере кристалла CsCl;

2. Запрограммировать расчёт зависимости структурной суммы от числа координационных оболочек для кристалла с объёмноцентрированной структурой;

3. Запрограммировать расчёт зависимости квантовых размерных эффектов от числа координационных оболочек для кристалла с объёмноцентрированной структурой.

4. Получить графические 3D модели кристаллической решётки с объёмноцентрированной структурой.

Актуальность работы: На современном этапе развития науки считаем актуальным рассмотрение методов создания кристаллов с наноструктурой. Так как наноматериалы находят всё большее применение в различных сферах деятельности человека (медицина, авиастроение, космонавтика и т.д.).

Математическая модель структуры для больших кристаллов выражается постоянной Маделунга, которая вычисляется исходя из сходимости ряда (Методы предложенные О. Эмерслебеном (метод прямого суммирования), Х. Эвьеном, П. Эвальдом, У. Харрисоном).

Но для рассмотрения кристаллов с малым числом частиц, для учёта дефектов и самое главное для создания кристаллов с наноструктурой (1D, 2D, 3D) такие методы не подходят. В связи с этим в нашей работе, предлагается векторный метод компьютерного моделирования. С помощью такого метода можно не только учесть дефекты, точно рассчитать энергию связи, но и рассчитать квантоворазмерные эффекты, а в перспективе запрограммировать создание будущего кристалла с любой структурой.

В данной работе выведены формулы суммы для вычисления структурного коэффициента малых кристаллов. Для расчета структурного коэффициента применяется векторный метод компьютерного моделирования. Благодаря этому методу в представленной работе также приводится пример для расчёта квантоворазмерных эффектов 3D нанокристаллов.

Выводы, сделанные в этой работе, возможно, будут полезны в нанотехнологии, при создании наноматериалов, анализе и расчёте дефектов кристаллов.

Физические свойства и энергия кристалла

Обоснование векторного метода

Физические свойства и энергия кристаллов

Объектом исследования настоящей работы является решётка ионных кристаллов обьёмноцентрированной структуры (рис. 1).

Известно, что механические, оптические, электрические и другие свойства зависят от структуры т.е. от расположения частиц, образующих кристалл.

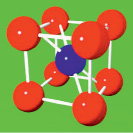
Рис. 1. Элементарная ячейка объёмноцентрированной структуры

Так, например – энергия связи ионного кристалла зависит от структуры кристалла [3, 5].

Найдём энергию взаимодействия i-го иона со всеми другими ионами [3, 5]:

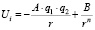(1.1.1)

Здесь

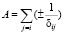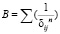, (1.1.2)

структурные суммы. Структурная сумма А получила название постоянной Маделунга [1].

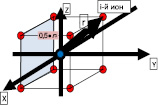
Рис. 2. Кристаллическая решётка ОЦК – Ион Cs+, – Ион Cl-

Краткое обоснование векторного метода для определения структурного коэффициента кристалла с малым числом частиц

Числитель структурной суммы

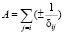
показывает количество ионов окружающих выбранный i-й ион, а знаменатель показывает расстояние от i-го иона до окружающих. Это расстояние можно определить векторной суммой проекций в трёхмерной системе координат (рис. 2).

,

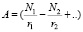
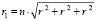где r – 0,5 базиса элементарной ячейки n-целые числа. Такой метод определения структурного коэффициента, мы назвали – векторным.

Математическая модель объёмноцентрированной структуры кристалла описанная с помощью векторного метода

Структурная сумма α

Рассмотрим изменение энергии i-го иона при росте кристалла, т.е. при достраивании ионных «оболочек».

Для этого в формулу (1.3) вместо структурной суммы кристалла А нужно подставлять структурную сумму отдельной оболочки. Обозначим структурную сумму отдельной оболочки – α.

Разделим все ионы решётки на 3 отдельные группы k ионы находящиеся по углам кристаллической решётки, j ионы находящиеся по рёбрам кристаллической решётки и i ионы находящиеся по граням кристаллической решётки. Тогда структурная сумма α будет выражаться формулой:

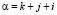(3.1.1)

Рассчитаем структурную сумму α для простой кристаллической решётки на примере Cs+Cl–.

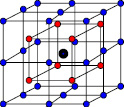
Рис. 3. Кристаллическая решётка – Ион Cs+, – Ион Cl–

Расчёт k ионов

Из рис. 3 видно, что на каждой из оболочек угловых ионов k будет по 8 ионов на расстоянии ri·m где r расстояние от выбранного иона до ионной оболочки (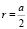, a – постоянная решётки), причём при m (номер оболочки) нечётных это будут ионы Cs+, а при m чётных это будут ионы Cl–, следовательно

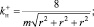(3.2.1)

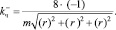(3.2.2)

Расчёт j ионов

J ионы располагаются на рёбрах. Из рис. 4 видно, что начиная с оболочки m = 2 и m = 4 по всем остальным чётным m будут слагаемые (только ионы Cl–)

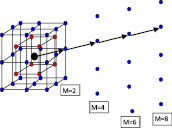
Рис. 4. Крист. решётка – Ион Cs+, – Ион Cl–

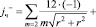
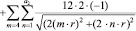(3.3.1)

где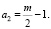

Чтобы рассчитать j нечётные обратимся к рис. 5. Из рисунка видно, что на нечётных m будут только ионы Cs+ (на чинная с оболочки 3 так как на m = 1 все ионы учтены коэффициентом k).

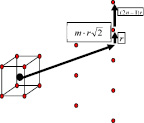
Рис. 5. Кристаллическая решётка ОЦК – Ион Cs+, – Ион Cl–

Т.е. появляется слагаемое:

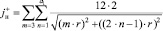(3.3.4)

где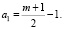

Этим слагаемым учитываются все ионы j находящиеся на нечётных оболочках.

Расчет i ионов

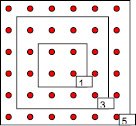
Рис. 6. Ионы Cs+ на гранях нечётных оболочек

Ионы первой оболочки учтены слагаемым 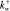, начиная с m = 3 (рис. 6) появляются другие ионы, которые учитываются слагаемым:

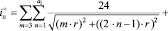
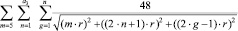(3.4.1)

где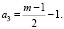

На чётных оболочках находятся ионы Cl– (рис. 7).

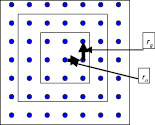
Рис. 7. Ионы Cl– на гранях чётных оболочек

В этом случае появятся слагаемые с оболочек m = 2,4,6:

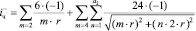
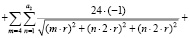
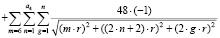(3.4.2)

где ;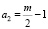

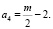
Расчёт структурных сумм и квантоворазмерных эффектов при помощи компьютерного моделирования

Расчёт структурных сумм при помощи компьютерного моделирования

Если значения 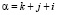присвоить координате y, а значение m координате x, то получим график зависимости структурной суммы от координационного числа оболочек. Выполнения таких расчётов подсилу только ЭВМ. В нашей работе для расчётов и построения графиков использовалась среда программирования PascalABC. График зависимости структурной суммы от количества координационных оболочек (m) представлен на рис. 8.

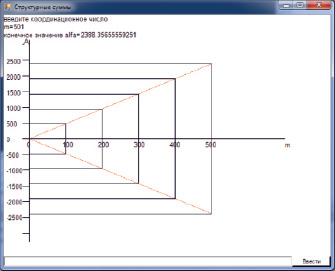
Рис. 8. График зависимости структурной суммы А от координационного числа оболочек m для кристалла типа CsCl, полученный в нашей работе

Программа для построения графика зависимости квантово-размерных эффектов (в процентах) от количества координационных оболочек кристалла

program Effekt;

Uses crt,graphABC;

label nachalo,1,2,3,4,5,6,koncicla,konec;

var n,m,Mmax,mn,mch,q,gd,gm,mx,alfay,msot,mtext,x1,y1,effekty:integer;

kpn,koch,joch1,joch2,jpn,ipn1,ipn2,ioch1,ioch2,ioch3,ioch4,jpnO,ipn1O,joch2O,

ioch2O,ioch3O,ipn2O,ioch4O,alfa,alfak,

a1,a2,a3,a4,kpnk,kochk,joch1k,ioch1k,jpnk,ipn1k,joch2k,ioch2k,

ioch3k,ipn2k,ioch4k,c,postMadelunga,chislo,effekt,a,r,n3,alfast,alfaSR:real;

s,s1,s2,s3,pm:string;

Begin

SetWindowCaption(‘Iaiiaciaiua yooaeou’);

nachalo: writeln(‘Mmax’);

read(Mmax);

if Mmax<0 then begin writeln(‘aaaaeoa iieieoaeuiia enei’);

goto nachalo;end;

mtext:=0;x1:=5;

repeat

str(mtext:3,s1);

mtext:=mtext+5; gotoxy (x1,24); write (s1);

x1:=x1+3;

until mtext>100;

chislo:=0;x1:=24;

repeat

chislo:=chislo+5;x1:=x1-1;str(chislo:2:0,s1); gotoxy (5,x1); write (s1);

until chislo>=100;

gotoxy(8,4);writeln(‘ %’); gotoxy(70,24);writeln(‘m’);

gotoxy(1,2);

m:=1; alfak:=0; r:=1; alfa:=0;

REPEAT

mn:=m; mch:=m;

kpn:=8;

if m<2 then goto 2;

koch:=8;

joch1:=12;

ioch1:=6;

if m<3 then GOTO 3;

n:=0; a1:=((m+1)/2)-1; jpnO:=0;

repeat

n:=n+1;

jpn:=12*2;

jpnO:=jpnO+jpn;

until n>a1-1;

n:=0; ipn1O:=0;

repeat

n:=n+1;

ipn1:=12*2;

ipn1O:=ipn1O+ipn1;

until n>a1-1;

if m<4 then GOTO 4;

n:=0; a2:=(m/2)-1; joch2O:=0;

repeat

n:=n+1;

joch2:=24;

joch2O:=joch2O+joch2;

until n>a2-1;

n:=0; ioch2O:=0;

repeat

n:=n+1;

ioch2:=24;

ioch2O:=ioch2O+ioch2;

until n>a2-1;

n:=0; ioch3O:=0;

repeat

n:=n+1;

ioch3:=24;

ioch3O:=ioch3O+ioch3;

until n>a2-1;

if m<5 then GOTO 5;

n:=0;

a3:=((m-1)/2)-1; ipn2O:=0;

repeat q:=0; n:=n+1;

repeat

q:=q+1;

ipn2:=48; ipn2O:=ipn2O+ipn2;

until q>n-1;

Until n>a3-1;

if m<6 then GOTO 6;

n:=0;

ioch4O:=0; a4:=(mch/2)-2;

repeat q:=0; n:=n+1;

repeat

q:=q+1; ioch4:=48; ioch4O:=ioch4O+ioch4;

until q>n-1;

Until n>a4-1;

goto konec ;

1:kpn:=0;

2:koch:=0;joch1:=0;ioch1:=0;

3:jpnO:=0;ipn1O:=0;

4:joch2O:=0;ioch2O:=0;ioch3O:=0;

5:ipn2O:=0;

6:ioch4O:=0;

konec:

koncicla:

If frac(m/2)=0 then begin kpn:=0;jpnO:=0;ipn1O:=0;ipn2O:=0;end

else

{if frac((m-1)/2)=0 then} begin koch:=0; joch1:=0;ioch1:=0; joch2O:=0;ioch2O:=0; ioch3O:=0; ioch4O:=0;

end;

alfa:=kpn+koch+joch1+ioch1+jpnO+ipn1O+joch2O+ioch2O+ioch3O+ipn2O+ioch4O;

alfast:=alfak;

alfak:=alfak+alfa+1; postMadelunga:=alfak;

effekt:=alfa*100/alfak;

alfaSR:=(alfak-alfast)/2;

mx:=Round(m*4.7)+50;

effekty:=375-Round((effekt*3.2));

putpixel(mx,effekty,3);

line(50,effekty,mx-1,effekty); m:=m+1;

UNTIL m >Mmax; str(mx:4,s2); alfast:=alfak;

writeln(‘’);

write(‘effekt:=’,effekt:2:1,’ %’);

line(50,380,50,50);line(50,380,550,380);

readln;readln;

end.

Полученные данные вполне согласуются с данными научной работы кандидата физико-математических наук И.Е. Ерёмина [1, с. 15], что говорит о справедливости полученных данных (рис. 9).

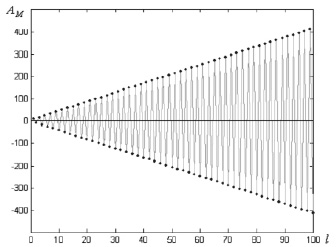
Рис. 9. График зависимости структурной суммы А от координационного числа оболочек m для кристалла типа CsCl в работе И.Е. Ерёмина, канд. физ.-мат. Наук, М.С. Сычёв. «Модифицированный алгоритм улучшения сходимости решёточных сумм» [2].

Что такое квантоворазмерные эффекты

При переходе вещества в наносостояние, его свойства начинают сильно зависеть от размера составляющих его нанообъектов, что является следствием происходящего при уменьшении размера объектов изменения их свойств и характера взаимодействия с другими объектами. В этом заключаются размерные эффекты, которые возникают, когда размер объекта становится сопоставимым с каким-то параметром вещества, оказывающим значительное влияние на протекание тех или иных процессов в веществе и, соответственно, на его свойства [2, с. 13).

Определение квантоворазмерных эффектов

При оценке возможного влияния размерных эффектов на свойства нанообъекта важным показателем является отношение числа атомов, находящихся на поверхности, к их общему количеству в объекте (4.3.1) [3, с. 14).

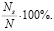(4.3.1)

Так как приведённые в предыдущих главах выводы позволяют определить структурные суммы и для каждого координационного слоя и для кристалла в целом, то эти же выводы позволяют определять количество частиц внешнего координационного слоя и всего кристалла. А значит можно определить квантово-размерные эффекты для рассмотренного типа кристаллической структуры.

Для расчёта и построения графика зависимости квантоворазмерных эффектов использовалось программирование в среде Pascal.

Программа для построения графика зависимости квантово-размерных эффектов (в процентах) от количества координационных оболочек кристалла

program Effekt;

Uses crt,graphABC;

label nachalo,1,2,3,4,5,6,koncicla,konec;

var n,m,Mmax,mn,mch,q,gd,gm,mx,alfay,msot,mtext,x1,y1,effekty:integer;

kpn,koch,joch1,joch2,jpn,ipn1,ipn2,ioch1,ioch2,ioch3,ioch4,jpnO,ipn1O,joch2O,

ioch2O,ioch3O,ipn2O,ioch4O,alfa,alfak,

a1,a2,a3,a4,kpnk,kochk,joch1k,ioch1k,jpnk,ipn1k,joch2k,ioch2k,

ioch3k,ipn2k,ioch4k,c,postMadelunga,chislo,effekt,a,r,n3,alfast,alfaSR:real;

s,s1,s2,s3,pm:string;

Begin

SetWindowCaption(‘Iaiiaciaiua yooaeou’);

nachalo: writeln(‘Mmax’);

read(Mmax);

if Mmax<0 then begin writeln(‘aaaaeoa iieieoaeuiia enei’);

goto nachalo;end;

mtext:=0;x1:=5;

repeat

str(mtext:3,s1);

mtext:=mtext+5; gotoxy (x1,24); write (s1);

x1:=x1+3;

until mtext>100;

chislo:=0;x1:=24;

repeat

chislo:=chislo+5;x1:=x1-1;str(chislo:2:0,s1); gotoxy (5,x1); write (s1);

until chislo>=100;

gotoxy(8,4);writeln(‘ %’); gotoxy(70,24);writeln(‘m’);

gotoxy(1,2);

m:=1; alfak:=0; r:=1; alfa:=0;

REPEAT

mn:=m; mch:=m;

kpn:=8;

if m<2 then goto 2;

koch:=8;

joch1:=12;

ioch1:=6;

if m<3 then GOTO 3;

n:=0; a1:=((m+1)/2)-1; jpnO:=0;

repeat

n:=n+1;

jpn:=12*2;

jpnO:=jpnO+jpn;

until n>a1-1;

n:=0; ipn1O:=0;

repeat

n:=n+1;

ipn1:=12*2;

ipn1O:=ipn1O+ipn1;

until n>a1-1;

if m<4 then GOTO 4;

n:=0;a2:=(m/2)-1;joch2O:=0;

repeat

n:=n+1;

joch2:=24;

joch2O:=joch2O+joch2;

untiln>a2-1;

n:=0;ioch2O:=0;

repeat

n:=n+1;

ioch2:=24;

ioch2O:=ioch2O+ioch2;

untiln>a2-1;

n:=0;ioch3O:=0;

repeat

n:=n+1;

ioch3:=24;

ioch3O:=ioch3O+ioch3;

until n>a2-1;

if m<5 then GOTO 5;

n:=0;

a3:=((m-1)/2)-1; ipn2O:=0;

repeat q:=0; n:=n+1;

repeat

q:=q+1;

ipn2:=48;

ipn2O:=ipn2O+ipn2;

until q>n-1;

Until n>a3-1;

ifm<6thenGOTO6;

n:=0;

ioch4O:=0;a4:=(mch/2)-2;

repeatq:=0;n:=n+1;

repeat

q:=q+1;

ioch4:=48;

ioch4O:=ioch4O+ioch4;

untilq>n-1;

Untiln>a4-1;

gotokonec;

1:kpn:=0;

2:koch:=0;joch1:=0;ioch1:=0;

3:jpnO:=0;ipn1O:=0;

4:joch2O:=0;ioch2O:=0;ioch3O:=0;

5:ipn2O:=0;

6:ioch4O:=0;

konec:

koncicla:

Iffrac(m/2)=0then begin kpn:=0;jpnO:=0;ipn1O:=0;ipn2O:=0;end

else

{if frac((m-1)/2)=0 then} begin koch:=0; joch1:=0;ioch1:=0; joch2O:=0;ioch2O:=0; ioch3O:=0;

ioch4O:=0;

end;

alfa:=kpn+koch+joch1+ioch1+jpnO+ipn1O+joch2O+ioch2O+ioch3O+ipn2O+ioch4O;

alfast:=alfak;

alfak:=alfak+alfa+1;postMadelunga:=alfak;

effekt:=alfa*100/alfak;

alfaSR:=(alfak-alfast)/2;

mx:=Round(m*4.7)+50;

effekty:=375-Round((effekt*3.2));

putpixel(mx,effekty,3);

line(50,effekty,mx-1,effekty);

m:=m+1;

UNTILm>Mmax;str(mx:4,s2);alfast:=alfak;

writeln(‘’);

write(‘effekt:=’,effekt:2:1,’ %’);

line(50,380,50,50);line(50,380,550,380);

readln;readln;

end.

Результаты вычислений и графики (см. рис. 10), полученные с помощью программирования по векторному методу, совпадают с результатами, приведёнными в работе Новикова Л.С., Ворониной Е.Н. «Перспективы применения наноматериалов в космической технике». Учебное пособие. – Москва: Университетская книга, 2008. – 188 с. [3] (см. рис. 11).

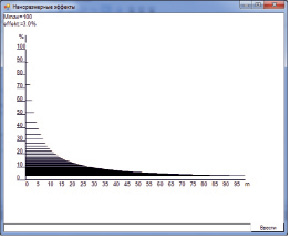
Рис. 10. График зависимости наноразмерного эффекта (в процентах) от координационного числа оболочек m для кристалла типа CsCl, полученный в нашей работе

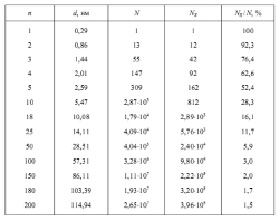
Рис. 11. Таблица зависимости наноразмерного эффекта (в процентах) от координационного числа оболочек m

Заключение

Результаты вычислений и графики, полученные с помощью программирования по векторному методу, подтверждают справедливость этого метода.

Целью работы было создание математической модели структуры кристалла векторным методом прямого суммирования. Математическая модель структуры кристалла выведена формулами суммы для ОЦК (объёмноцентрированных кристаллов) на примере кристалла CsCl. Эти формулы позволяют рассчитать структурную сумму кристаллов любого числа частиц. Особую роль такой подход к расчёту энергии играет при рассмотрении малых кристаллов.

С помощью предложенной программы, направленной на расчёт структурной суммы в кристалле, можно проследить не только общий вид изменения энергии, но и влияние каждой ионной «оболочки» с точным расчётом. Как было сказано выше, предложенная модель может учесть влияние даже точечных дефектов в кристаллах, что поможет в различных видах диагностики примесей, «чистоты» кристаллов. Но главным применением описанного выше векторного метода считаем возможность запрограммированного роста кристалла, создание базы данных различных материалов, создание материалов с наноструктурами типов 0D, 1D, 2D, 3D.

Задачи, поставленные в работе можно считать выполненными, т.к. нам удалось запрограммировать вычисления структурных сумм, а так же наноразмерного эффекта для выбранного типа структуры кристалла.

Получение графических моделей кристаллов, выходит за рамки норм объёма работы, т.к. требует дополнительные выводы, поэтому считаем целесообразным эту задачу выполнить в следующей работе.

А в перспективе, мы надеемся, что с помощью выводов сделанных в этой работе, станет возможным запрограммированное создание наноматериалов любой структуры с заданными свойствами.

Мы считаем, что с применением устройства сочетающего в себе свойства молекулярного зонда и 3D принтера, возможно построение будущего нанокристалла.

Библиографическая ссылка