Топология, на мой взгляд, является одной из интереснейших наук нашего времени, ведь столько неизведанного и увлекательного можно найти в ней. Именно поэтому мой выбор пал на нее, а вследствие более детального изучения этой науки меня заинтересовала теорема Эйлера.
Эта знаменитая теорема впервые появилась в 1752 году в журнале Петербургской академии наук в работах Леонарда Эйлера «Элементы учения о телах» и «Доказательство некоторых замечательных свойств, которым подчинены тела, ограниченные плоскими гранями».
Теорема Эйлера хорошо известна и присутствует в школьном курсе математики, Однако там она, как правило, жестко связана с изучением многогранников и используется в основном для выяснения того, какие правильные многогранники могут существовать. Такой подход создает превратное впечатление о роли и месте теоремы Эйлера: остается невскрытой чисто топологическая сущность этой теоремы и ее роль в классификации поверхностей, не выясняется связь эйлеровой характеристики с родом поверхности. В результате возникают потери и для приложений: распространение теоремы Эйлера на более сложные, чем обычные многогранники, объекты (сферы с «ручками», многогранники с «дырками» и т.д.) остается вне школьных факультативов. Изучение топологии до сих пор является актуальным. Так совсем недавно, в 2016 году, Дэвид Таулес, Дункан Холдейн и Майкл Костерлитц стали лауреатами Нобелевской премии за результаты, для получения которых они существенно применили идеи топологии.
Пользуясь формулой Эйлера я показываю в своей работе, что каждую ориентируемую поверхность данного рода можно представить в виде многогранника, являющегося границей тела, полученного удалением из заполненного куба конечного числа сквозных заполненных параллелепипедов. То есть представить любую ориентируемую поверхность (с точностью до гомеоморфизма) с помощью объектов хорошо изученных школьной программой и названных мной кубами с конечным числом сквозных «дырок».
Таким образом, можно определить объект и предмет данной исследовательской работы.
Объект исследования: теорема Эйлера.
Предмет исследования: использование теоремы Эйлера для представления ориентируемой поверхности в виде многогранника, являющегося границей тела, полученного удалением из заполненного куба конечного числа сквозных заполненных параллелепипедов.
Цели: Найти взаимосвязь между многогранниками, изучаемыми в школе и топологической классификацией ориентируемых поверхностей.
Задачи:
1. Рассмотреть научно-историческую литературу по теме.
2. Ввести класс многогранников (кубов с конечным числом «дырок», представляющих топологические типы всех ориентируемых поверхностей).
3. С помощью метода математической индукции вывести формулу, для вычисления эйлеровой характеристики каждого многогранника, из рассматриваемого класса.
Правильные многогранники и почему их всего 5
Многогранник – это множество М плоских выпуклых многоугольников – граней, расположенных в пространстве так, что:
1. Каждая сторона любого многоугольника является стороной в точности еще одного многоугольника из М. Эта сторона, общая для двух многоугольников, называется ребром, а многоугольники, имеющие общее ребро, называются смежными.
2. От каждого многоугольника из М к любому другому можно пройти по цепочке многоугольников из М, в которой каждые два последовательных многоугольника, являются смежными.
3. Если два многоугольника имеют общую вершину, то такую цепочку можно составить из многоугольников, каждый из которых содержит эту вершину.
Напомним, что гомеоморфизмом называется взаимно однозначное и взаимно непрерывное отображение топологических пространств [18].
Правильные многогранники
Определение: Выпуклый многогранник называется правильным, если его грани являются правильными многогранниками с одним и тем же числом сторон и в каждой вершине многогранника сходится одно и то же число ребер.
Всего существует пять видов правильных выпуклых многогранников. Их гранями являются правильные треугольники, правильные четырёхугольники (квадраты) и правильные пятиугольники.
Докажем, что не существует правильного многогранника, гранями которого являются правильные шестиугольники, семиугольники и, вообще, n – угольники при n ≥6.
В самом деле, угол правильного n – угольника при n ≥ 6 не меньше 120 градусов.
С другой стороны, при каждой вершине многогранника должно быть не менее трёх плоских углов. Поэтому если бы существовал правильный многогранник, у которого грани – правильные n-угольники при n ≥ 6, то сумма плоских углов при каждой вершине такого многогранника была бы не меньше чем 360 градусов. Но это невозможно, так как сумма всех плоских углов при каждой вершине выпуклого многогранника меньше 360 градусов.
По этой же причине каждая вершина правильного многогранника может быть вершиной либо трёх, четырёх или пяти равносторонних треугольников, либо квадратов, либо трёх правильных пятиугольников. Других возможностей нет. В соответствии с этим получаем следующие правильные многогранники, их всего 5.
Правильный тетраэдр составлен из четырёх равносторонних треугольников. Каждая его вершина является вершиной трёх треугольников. Следовательно, сумма плоских углов при каждой вершине равна 180 градусам.
Правильный октаэдр составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырёх треугольников. Следовательно, сумма плоских углов при каждой вершине равна 240 градусам.
Правильный икосаэдр составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной пяти треугольников. Следовательно, сумма плоских углов при каждой вершине равна 300 градусам.
Куб (гексаэдр) составлен из шести квадратов. Каждая вершина куба является вершиной трёх квадратов. Следовательно, сумма плоских углов при каждой вершине равна 270 градусам.
Правильный додекаэдр составлен из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников. Следовательно, сумма плоских углов при каждой вершине равна 324 градусам.
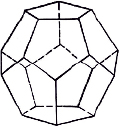
Названия этих многогранников пришли из Древней Греции, и в них указывается число граней:
«эдра» – грань, «тетра» – 4, «гекса» – 6, «окта» – 8, «икоса» – 20, «додека» – 12.
Л. Шлефли (1814–1895), швейцарский математик которому принадлежит немало изящных результатов в геометрии и математическом анализе предложил обозначение {p, q}, где: p – число сторон каждой грани, q – число рёбер, сходящихся в каждой вершине.
Символы Шлефли для правильных многогранников приведены в табл. 2.
Правильные многогранники в научных фантазиях разных учёных. «Правильные многогранники в философской картине мира Платона»
Правильные многогранники иногда называют Платоновыми телами, поскольку они занимают видное место в философской картине мира, разработанной великим мыслителем Древней Греции Платоном (ок. 428 – ок. 348 до н.э.).
Платон считал, что мир строится из четырёх «стихий» – огня, земли, воздуха и воды, а атомы этих «стихий» имеют форму четырёх правильных многогранников. Тетраэдр олицетворял огонь, поскольку его вершина устремлена вверх, как у разгоревшегося пламени; икосаэдр – как самый обтекаемый – воду; куб – самая устойчивая из фигур – землю, а октаэдр – воздух. В наше время эту систему можно сравнить с четырьмя состояниями вещества – твёрдым, жидким, газообразным и пламенным. Пятый многогранник – додекаэдр символизировал весь мир и почитался главнейшим.
Это была одна из первых попыток ввести в науку идею систематизации.
Изучение платоновых тел и связанных с ними фигур продолжается и поныне. И хотя основными мотивами современных исследований служат красота и симметрия, они имеют также и некоторое научное значение, особенно в кристаллографии. Кристаллы поваренной соли, тиоантимонида натрия и хромовых квасцов встречаются в природе в виде куба, тетраэдра и октаэдра соответственно. Икосаэдр и додекаэдр среди кристаллических форм не встречаются, но их можно наблюдать среди форм микроскопических морских организмов, известных под названием радиолярий.
«Формула Эйлера»
Работа Эйлера началась с того, что он составил большую таблицу, в которой выписал значения величин V, E, F для конкретных многогранников. Острая наблюдательность позволила ему в этом массиве чисел обнаружить отмеченную закономерность. В 1751 году он дал доказательство этой формулы для выпуклых многогранников.
Таблица 1
Сводная таблица правильных многогранников
|
Тип правильного многогранника |
Число сторон у грани |
Число рёбер, примыкающих к вершине |
Общее число вершин |
Общее число рёбер |
Общее число граней |
|
Тетраэдр |
3 |
3 |
4 |
6 |
4 |
|
Гексаэдр или Куб |
4 |
3 |
8 |
12 |
6 |
|
Октаэдр |
3 |
4 |
6 |
12 |
8 |
|
Додекаэдр |
5 |
3 |
20 |
30 |
12 |
|
Икосаэдр |
3 |
5 |
12 |
30 |
20 |
Таблица 2
|
Тип правильного многогранника |
Общее число вершин |
Общее число рёбер |
Общее число граней |
Символ Шлефли |
|
Тетраэдр |
4 |
6 |
4 |
{3, 3} |
|
Гексаэдр или Куб |
8 |
12 |
6 |
{4, 3} |
|
Октаэдр |
6 |
12 |
8 |
{3, 4} |
|
Додекаэдр |
20 |
30 |
12 |
{5, 3} |
|
Икосаэдр |
12 |
30 |
20 |
{3, 5} |
Таблица 3
|
Правильный многогранник |
Число |
||
|
граней |
вершин |
рёбер |
|
|
Тетраэдр |
4 |
4 |
6 |
|
Куб |
6 |
8 |
12 |
|
Октаэдр |
8 |
6 |
12 |
|
Додекаэдр |
12 |
20 |
30 |
|
Икосаэдр |
20 |
12 |
30 |
Таблица 4
|
Правильный многогранник |
Число |
||
|
граней и вершин (Г + В) |
рёбер (Р) |
рёбер |
|
|
Тетраэдр |
4 + 4 = 8 |
6 |
6 |
|
Куб |
6 + 8 = 14 |
12 |
12 |
|
Октаэдр |
8 + 6 = 14 |
12 |
12 |
|
Додекаэдр |
12 + 20 = 32 |
30 |
30 |
|
Икосаэдр |
20 + 12 = 32 |
30 |
30 |
Анализируя табл. 1, возникает вопрос: «Нет ли закономерности в возрастании чисел в каждом столбце?» По-видимому, нет. Например, в столбце «грани» казалось бы, просматривается закономерность (4 + 2 = 6, 6 + 2 = 8), но затем намеченная закономерность нарушается (8 + 2? 12, 12 + 2? 20). В столбце «вершины» нет даже стабильного возрастания.
Число вершин то возрастает (от 4 до 8, от 6 до 20), а то и убывает (от 8 до 6, от 20 до 12). В столбце «рёбра» закономерности тоже не видно (табл. 3).
Но можно рассмотреть сумму чисел в двух столбцах, хотя бы в столбцах «грани» и «вершины» (Г + В). Составим новую таблицу своих подсчётов (табл. 4).
Вот теперь закономерности может не заметить только «слепой». Сформулируем её так: «Сумма числа граней и вершин равна числу рёбер, увеличенному на 2», т.е. Г + В = Р + 2, или, Г + В – Р = 2
Итак, мы «открыли» формулу, которая была подмечена уже Декартом в 1640 г., а позднее вновь открыта Эйлером (1752), имя которого с тех пор она носит. Формула Эйлера верна для любых выпуклых многогранников.
Рассматриваемые многогранники гомеоморфны поверхности сферы, которую называют поверхностью рода ноль. Как оказалось, формула Эйлера имеет место для любой поверхности рода ноль, если ее представить в виде многогранника (криволинейного).
Теорема 1. Для всякого многогранника представляющего поверхность рода ноль имеет место формула. V – Е + F = 2.
Формула Эйлера для поверхностей
Введем понятие поверхности и рода поверхности
Поверхность
Определение 1. Фигура, у которой каждая точка х имеет окрестность, гомеоморфную открытому кругу (внутри которого лежит точка х), называется двумерной поверхностью без края или замкнутой поверхностью.
Примером таких поверхностей является сфера (рис. 1) и тор (рис. 2).

Рис. 1

Рис. 2
Рассматривают также поверхности с краем. Замкнутый круг – это поверхность с краем. Сфера, из которой удалены несколько открытых кругов (рис. 3), также является поверхностью с краем.
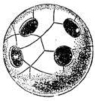
Рис. 3
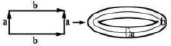
Рассмотрим другие примеры двумерных поверхностей на наглядных примерах: следующие поверхности можно получить, склеивая противоположные стороны прямоугольника. Склеиваемые стороны обозначаются одинаковыми буквами и стрелками в зависимости от направления склеивания.
Ручка.
Ручка является поверхность с краем.

Тор.
Тор является поверхностью без края.
Род поверхности. Многие простые, но весьма существенные обстоятельства выясняются при изучении двумерных поверхностей. Сравним, например, поверхность сферы с поверхностью тора. Взглянув на рис. 4, сразу можно обнаружить различие: на сфере, как и на плоскости, замкнутая кривая вроде С разделяет поверхность на две части; но на торе существуют и такие замкнутые кривые, например С', которые не разделяют поверхности на две части
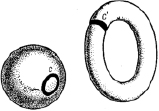
Рис. 4. Разрезы на сфере и на торе
Если мы говорим, что кривая С разделяет сферу на две части, то это означает, другими словами, что при разрезании поверхности сферы по кривой C эта поверхность распадается на два не связанных между собой куска, или еще, иначе, что можно найти две такие точки сферы, что всякая кривая на сфере, их соединяющая, непременно пересечется с кривой.Напротив, если разрезать тор по кривой С', то после разреза поверхность не распадется: любые две ее точки можно соединить кривой, не имеющей общих точек с С'. Указанное различие свидетельствует о том, что сфера и тор в топологическом смысле не принадлежат одному и тому же классу поверхностей: тор нельзя топологически (то есть с помощью гомеоморфизма) преобразовать в сферу. Рассмотрим теперь поверхность, изображенную на рис. 5.
На этой поверхности оказывается возможным провести сразу две замкнутые кривые, A и B, которые не разделяют поверхности на части. Тор, напротив, при проведении двух таких кривых непременно разделится на части. С другой стороны, любые три замкнутые кривые разделяют нашу поверхность. Все это подсказывает мысль ввести понятие рода поверхности.
Определение 2. Родом поверхности называется наибольшее возможное число взаимно не пересекающихся замкнутых кривых (без самопересечений), которые можно провести на поверхности, не разделяя ее на части.

Рис. 5. Поверхность рода 2
Род сферы равен 0, род тора равен 1, род поверхности, изображенной на рис. 5, равен 2.
Род есть топологический инвариант поверхности: он не изменяется при гомеоморфизме (топологическом преобразовании, деформировании) поверхности. Обратно, можно доказать (но мы не приводим здесь этого доказательства), что если две замкнутые ориентируемые поверхности имеют один и тот же род, то одну поверхность можно гомеоморфно (топологически) отобразить в другую (иногда говорят деформировать); таким образом род p = 0, 1, 2, . . . замкнутой поверхности полностью характеризует топологический класс, к которому она принадлежит. Здесь предполагается, что мы рассматриваем только ориентируемые поверхности.

Рис. 6. Поверхности рода 2
Поверхность с p ручками есть поверхность рода p, поэтому любую из этих поверхностей можно взять в качестве «топологического представителя» всех замкнутых поверхностей рода p.
Эйлерова характеристика поверхности
Мы установили, что формула Эйлера справедлива для случая любого простого многогранника. Но эта формула не теряет смысла и значимости также и применительно к иным, гораздо более общим случаям: вместо многогранников элементарной геометрии с плоскими гранями и прямыми ребрами можно взять простые «многогранники», у которых «гранями» будут кривые поверхности, а «ребрами» – кривые линии, или можно нарисовать «грани» и «ребра» на поверхности, например, шара. Больше того, вообразим, что поверхность многогранника или сферы сделана из тонкого слоя резины; тогда формула Эйлера сохранится, как бы ни была деформирована рассматриваемая поверхность – путем изгибаний, сжатий, растяжений и т.д., – лишь бы резиновый слой не был порван.
Предположим, что замкнутая поверхность S рода p разбита на некоторое число областей: такое подразделение получается, если мы отметим на S ряд «вершин» и соединим их затем между собой дугами кривых. Мы скажем, что в этом случае поверхность является криволинейным многогранником.
Обозначим через В-число вершин, Р – число ребер и Г – число граней данного многогранника.
Теорема 2. Имеет место формула, являющаяся обобщением формулы Эйлера.
В – Р + Г = 2 – 2 р.
Практика
Вычисление эйлеровой характеристики многогранников, являющихся кубами с конечным числом «дырок»
Рассмотрим простой многогранник G0 рода ноль в виде стандартного куба. Вырежем из него параллелепипед так как указано на рисунке 6 .Тогда получим многогранник G1, который мы назовем кубом со сквозной «дыркой», или для краткости – кубом с одной дыркой (см рис. 7).
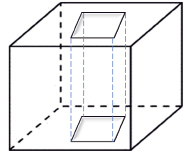
Рис. 7
Сделаем дополнительное построение, так как это указано на рис. 8 и вычислим эйлеровую характеристику χ = В – Р + Г, полученного многогранника, где В есть число вершин, Р – число ребер, а Г – число граней.
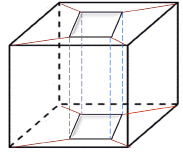
Рис. 8
Вычисления показывают, что число В вершин в данном многограннике равно 16, число Р ребер равно 32, а число Г граней равно 16. Тогда χ = В – Р + Г = 16 – 32 + 16 = 0. Как известно, в главе 2 теоремы 2 уже говорилось, что, эйлерова характеристика ориентируемой двумерной поверхности без края вычисляется по формуле χ = 2 – 2р, где p – род поверхности. Так как в нашем случае эйлерова характеристика получилась равной нулю, то отсюда следует, что полученный многогранник гомеоморфен двумерному тору.
Аналогично посчитаем эйлеровую характеристику у многогранника с двумя «дырами» (рис. 9).
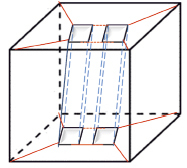
Рис. 9
Число вершин равно 24,число ребер равно 44,число граней равно 18. Посчитаем эйлеровую характеристику данного многогранника χ = 24 – 44 + 18 = – 2. Соответственно делаем вывод, что данный многогранник гомеоморфен кренделю рода 2,так как у кренделя эйлеровая характеристика (χ = 2 – 2р, где p равно2) равна – 2.
Проделаем ту же операцию с тремя «дырами» (рис. 10).
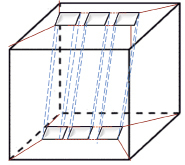
Рис. 10
Посчитаем эйлеровую характеристику у данного многогранника с тремя «дырами». Число вершин равно 32,число ребер равно 64,число граней равно 28.Посчитаем эйлеровую характеристику данного многогранника 32-64 + 28 = -4. Соответственно делаем вывод, что данный многогранник гомеоморфен кренделю рода 3 ,так как у кренделя эйлеровая характеристика (χ = 2 – 2р, где p равно 3) равна -4.
Предположим теперь, что мы проделали в кубе p сквозных дыр. И сделали разбиение на многоугольники методом, описанным на рассмотренных примерах. Выведем формулы для числа вершин ребер и граней описанного разбиения.
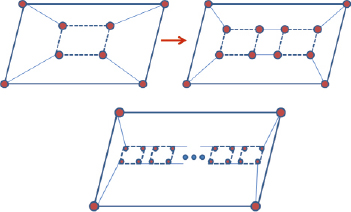
Рис. 11 (вид сверху)
Лемма 1. Число вершин вычисляется по формуле Вp = 8 + 8p.
Доказательство. Докажем данное утверждение методом математической индукции. Непосредственно проверяется, что формула верна, для p = 1, так как в этом случае В1 = 16, и это в точности равно числу вершин куба с одной «дыркой» . Предположим, что формула верна для числа «дырок» равного p. Докажем, что оно верна для p + 1.Действительно, при добавлении новой «дырки» число вершин увеличивается на 8 как на верху, так и внизу многоугольника, поэтому Вp + 1 = 8 + 8p + 8 = 8 + + 8(p + 1) (см. рис. 11). Лемма доказана.
Лемма 2. Число ребер вычисляется по формуле Рp = 16 + 16p.
Доказательство. Докажем данное утверждение методом математической индукции. Для p = 1 формула верна, так как в этом случае Р1 = 32, что совпадает с числом ребер куба с одной «дыркой». Предположим, что формула верна для числа «дырок» равного p. Докажем, что она верна для p + 1.Действительно, при добавлении новой «дырки» число ребер увеличивается на 16 как на верху, так и внизу многоугольника поэтому Рp + 1 = = 16 + 16p + 16 = 16 + 16(p + 1) (см. рис. 12). Лемма доказана.
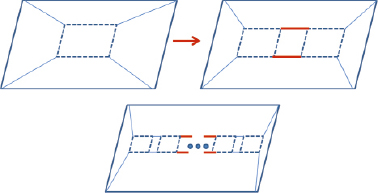
Рис. 12 (вид сверху)
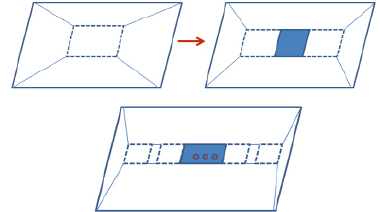
Рис. 13 (вид сверху)
Лемма 3. Число граней вычисляется по формуле Гp = 10 + 6p.
Доказательство. Докажем данное утверждение методом математической индукции. Для p = 1 формула верна, так как Г1 = 16, совпадает с числом граней куба с одной «дыркой». Предположим, что формула верна для числа «дырок» равного p. Докажем, что оно верна для p + 1.Действительно, при добавлении новой «дырки» число граней увеличивается на 6 как на верху, так и внизу многоугольника, поэтому Рp + 1 = 10 + 6p + 6 = 10 + 6(p + 1) (см. рис. 13). Лемма доказана.
Лемма 4. Эйлерова характеристика разбиения куба с p дырками вычисляется по формуле x = 2-2p.
Доказательство. Подставим данные из лемм 1-3 в формулу для вычисления эйлеровой характеристики и получим
x = 8 + 8p-(16 + 16p) + (10 + 6p) = 2-2p.
Лемма доказана.
Из лемм 1-4 следует основной результат нашей работы.
Следствие: Куб с конечным числом сквозных дыр гомеоморфен ориентируемой поверхности рода g = p.
Доказательство. Из утверждения главы 2 теоремы 2, эйлерова характеристика ориентируемой поверхности рода g вычисляется по формуле x = 2-2g. Отсюда и из леммы 4 следует, что g = p
Заключение
В ходе своей работы я решила поставленные мною задачи, а именно:
1. Рассмотрела научно-историческую литературу по теме.
2. Ввела класс многогранников (кубов с конечным числом «дырок», представляющих топологические типы всех ориентируемых поверхностей).
3. С помощью метода математической индукции вывела формулу, для вычисления эйлеровой характеристики каждого многогранника, из рассматриваемого класса.
В представленной работе, было получено представление всех классов топологически эквивалентных двумерных поверхностей моделями, представляющими из себя куб с конечным числом сквозных «дырок». При этом с помощью вычисления эйлеровой характеристики указанных моделей было установлено, что число «дырок» данной модели равно ее роду.
Библиографическая ссылка
Ивлиева А.А. ПРЕДСТАВЛЕНИЕ ОРИЕНТИРУЕМЫХ ПОВЕРХНОСТЕЙ МНОГОГРАННИКАМИ // Международный школьный научный вестник. 2017. № 3-1. ;URL: https://school-herald.ru/ru/article/view?id=233 (дата обращения: 15.10.2025).
