Международный школьный научный вестник

Научный журнал для старшеклассников и учителей ISSN 2542-0372

• Авторы
• Научный руководитель
• Файлы
• Литература

Авдонина М.А. 1 Гасанова К.А. 1 Терещенко А.И. 1

---

1 11 класс МБОУ СОШ № 21 г. Ногинск Московской области

Туманов В.Е. (г. Ногинск Московской области, МБОУ СОШ № 21)

Статья в формате PDF

0 KB

1. Алимов Ш.А., Колягин Ю.М., Ткачева М.В. и др. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа 10-11 классы: учебник для общеобразовательных организаций: базовый и углубленный уровни. – М.: Просвещение, 2014.

2. Семакин И.Г., Хеннер Е.К., Шеина Т.Ю. Информатика. Базовый уровень. Учебник для 10 класса. – М.: БИНОМ Лаборатория знаний, 2016.

3. Мудров А.Е. Численные методы для ПЭИМ на языках Бейсик, Фортран и Паскаль. – Томск: МП «РАСКО», 1991.

4. Дьяконов В.П. Справочник по алгоритмам и программам на языке бейсик для персональных ЭВМ. – М.: Наука. 1989.

В школьном куре математики вводится понятие производной функции одной переменной и изучаются формулы производных элементарных функций [1]. Однако при изучении языка программирования Pascal ABC численные методы численного дифференцирования функций одной переменной не рассматривается [2]. Поэтому разработка темы численного дифференцирования для использования при изучения языка Pascal ABC в школьном курсе информатики является актуальной задачей, решение которой расширяет межпредметные связи обучающихся.

Целью настоящей работы является использование алгоритмов численного дифференцирования гладких функций и функций, заданных таблично, при разработке программ для использования в организации проектной деятельности обучающихся на уроках информатики.

Задачами работы являлись: изучение принципов дифференцирования функций одной переменной на основе разложения функции одной переменной в ряд Тейлора, исследование алгоритмов численного дифференцирования функций одной переменной на предмет порядка ошибок и скорости сходимости, создание программ численного дифференцирования функций одной переменной для использования в учебном процессе.

Предметом исследования являлось создание комплекса подпрограмм на языке программирования Pascal ABC для численного дифференцирования функций одной переменной.

Гипотеза в рамках поставленной учебной задачи состоит в том, чтобы экспериментально доказать возможность разработки алгоритмов численного дифференцирования с высокой скоростью сходимости.

В настоящее время вопрос численного дифференцирования функций является практически решенным. Практическая значимость решения поставленной задачи носит учебный характер и зависит от возможностей языка программирования, в чем и состоял дидактический и развивающий компонент исследования. Обзор литературы по данному вопросу в рамках компетенцию авторов приведен в [3-4].

Постановка задачи и метод решения

По определению производная функция в точке x равна 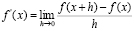[1]:

(1)

Поэтому при достаточно малых h (что будет верно), можно считать, что:

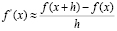(2)

Как показывает практика непосредственное использование формулы (2) дает не совсем корректные результаты. Причина состоит в том, что при численном дифференцировании следует учитывать ошибки округления.

Например, рассмотрим функцию:

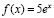(3)

И вычислим ее производную при x= 0 численно по формуле (2). Значение производной равно 5. Результаты вычислений при различных значения h приведены в Табл. 1.

Таблица 1

Результаты вычислений производной функции (3) при различных значениях h по формуле (2)

Как видно из Табл. 1 при уменьшении h вычисленное значение производной уменьшатся медленно. Как можно ускорить процесс вычисления производной?

Можно предположить, что проблема состоит в ошибке округления и конечной арифметике компьютера.

Рассмотрим ряд Тейлора [3]:

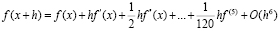(4)

где O(h6) означает величину порядка h6, т.е. ошибку указанного порядка, т.е. т.е. ошибку указанного порядка

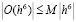
В предположении, что вторая производная не равна нулю, ошибка вычислений по формуле (2) будет порядка O(h), что не является хорошим приближением.

Как уменьшить ошибку? Исходя из формулы Тейлора (4), рассмотрим следующее приближение:

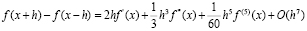
Откуда следует оценка для производной:

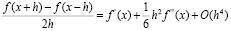
Ошибка будет порядка O(h2). Для пробной функции (3) имеем:

Таблица 2

Результаты вычислений производной функции (3) при различных значениях h по формуле (2).

Как видно из Табл. 2 скорость сходимости при вычислении возрастает. Можно еще уменьшить ошибку сходимости. Для этого рассмотрим функцию:

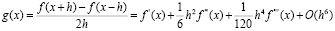
Тогда можно предположить, что линейная комбинация введенной функции при различных значениях h позволит уменьшить ошибку до O(h4)

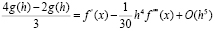
Откуда получаем выражение для вычисления производной

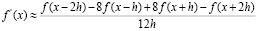(5)

которая дает значение производной нашей пробной функции 4.9999 при h=0.1 и 5.000 при h=0.01.

Проведенные рассуждения предполагали, что существует производная функции до 5-го порядка включительно и х принадлежит действительной оси. Если функция существует при x больше или равно нулю, справедлива формула для вычисление односторонней производной в 0, полученная путем аналогичных рассуждений:

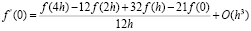
Для функций, заданных таблично со случайной погрешностью, точность численного дифференцирования может быть низкой. Это связно с тем, что может быть не известно априори, сколько производных существует у такой функции.

Основной принцип построения формул численного дифференцирования таких функций основывается на теореме, что гладкую функцию (у которой существует необходимое количество непрерывных производных) можно заменить полиномом подходящей степени и предположении, что производную такой функции можно заменить производными от полинома.

При равномерно расположенных узлах формулы численного дифференцирования зависят от количества узлов (значений функции в выбранных точках), обычно рассматривают 3, 4, 5 узлов [4].

Результаты и обсуждение

Результатом проведенной работы по разработке программ численного дифференцирования функций одной переменной стало создание пакета подпрограмм численного дифференцирования функций одной переменной, имеющих необходимое число производных для использование в учебной и проектной деятельности обучающих.

Приведем фрагмент программы на языке Pascal ABC, реализующий вычисления производной функции по формуле (5).

Program der01;

var df,x,h:double;

function Fx(z:real): real;

begin

Fx:=5*exp(z);

end;

function deriv(x,h:real):real;

begin

deriv:=(Fx(x-2*h)-8*Fx(x-h)+8*Fx(x+h)-Fx(x+2*h))/12/h;

end;

begin

x:=0;

h:=0.01;

df:=deriv(x,h);

writeln(df:8:4);

end.

Сходимость представленного алгоритма приведена в предыдущем разделе.

Заключение

В настоящей работе были проанализированы алгоритмы численного дифференцирования гладких функций и функций, заданных таблично, разработаны программы нВ языке программирования Pascal ABC для использования в организации проектной деятельности обучающихся на уроках информатики.

Разработанный комплекс программ вычисления производной действительной дифференцируемой достаточно раз функции позволяет решать задачу использования обучающимися межпредметных связей, способствует развитию компетенций обучающихся при изучении курса математики и информатики в старшей школе.

Библиографическая ссылка