Данная статья является реферативным изложением основной работы. Полный текст научной работы, приложения, иллюстрации и иные дополнительные материалы доступны на сайте III Международного конкурса научно-исследовательских и творческих работ учащихся «Старт в науке» по ссылке: https://www.school-science.ru/0317/7/28946.
Объекты проекта: целые рациональные уравнения и многочлены различных степеней.
Предмет проекта: теорема Виета как инструмент для решения уравнений и вычисления значений многочленов различных степеней.
Цель работы: создание электронного пособия, которое может быть использовано как при классно – урочной, так при дистанционной системе обучения, расширит знания и возможности учащихся по данной теме за пределы страниц школьного учебника, путём обобщения теоремы Виета для уравнений высших степеней и применения специальных методов решения задач.
Задачи:
1. На примере биографии великого ученого показать движущие силы научной мысли.
2. Сформулировать, доказать и научить использовать теорему Виета в стандартных математических задачах.
3. Исследовать возможность обобщения теоремы для уравнений высших степеней.
4. Рассмотреть нестандартные методы решения математических задач, используя теорему Виета.
5. Экспериментально убедиться в рациональности применения теоремы.
6. Предложить материалы проверки как для теоретической, так и для практической подготовленности учащихся.
7. Вызвать активный познавательный интерес, который позволит глубже изучить проблему.
Теорема Франсуа Виета и её значение в математике
Жизненный путь
Франсуа Виет – выдающийся французский математик XVI в., положивший начало алгебре как науке. По образованию и основной профессии – юрист, по склонности души – математик.Франсуа Виет родился в 1540 г. на юге Франции в небольшом городке Фантене-ле-Конт, что находится в 60 км от Ла Рошели, бывшей в то время оплотом французских протестантов-гугенотов. Большую часть жизни он прожил рядом с виднейшими руководителями этого движения, хотя сам оставался католиком. Отец Виета был юристом, а мать (Маргарита Дюпон) происходила из знатной семьи, что облегчило дальнейшую карьеру её сына.По традиции сын выбрал профессию отца и стал юристом, окончив университет в Пуату. В 1560 году двадцатилетний адвокат начал свою карьеру в родном городе, но через три года перешел на службу в знатную гугенотскую семью де Партене. Он стал секретарем хозяина дома и учителем его дочери двенадцатилетней Екатерины. Именно преподавание пробудило в молодом юристе интерес к математике.Когда ученица выросла и вышла замуж, Виет не расстался с ее семьей, а переехал с нею в Париж, где ему было легче узнать о достижениях ведущих математиков Европы.
Жизненный путь. На государственной службе
В 1571 году Виет перешел на государственную службу, став советником парламента, а затем советником короля Франции Генриха III.В ночь на 24 августа 1572 года в Париже произошла массовая резня гугенотов католиками, так называемая Варфоломеевская ночь. В ту ночь вместе со многими гугенотами погибли муж Екатерины де Партене и математик Рамус. Во Франции началась гражданская война.
Через несколько лет Екатерина де Партене снова вышла замуж. На сей раз, ее избранником стал один из видных руководителей гугенотов – принц де Роган. По его ходатайству в 1580 году Генрих III назначил Виета на важный государственный пост рекетмейстера, который давал право контролировать от имени короля выполнение распоряжений в стране и приостанавливать приказы крупных феодалов.
Генрих III
Находясь на государственной службе, Виет оставался ученым. К этому времени относятся свидетельства современников Виета о его огромной трудоспособности. В 1584 году по настоянию Гизов Виета отстранили от должности и выслали из Парижа. Именно на этот период приходится пик его творчества. Обретя неожиданный покой и отдых, ученый поставил своей целью создание всеобъемлющей математики, позволяющей решать любые задачи… И он справился со своей задачей…
Герцог Гиз
Интересные факты из жизни и деятельности ученого
Франсуа Виет, вычисляя периметры вписанного и описанного 322 216–угольников, получил 9 точных десятичных знаков.
Впервые обозначать десятичные дроби с помощью запятой предложил Франсуа Виет. До него изображение дробей было весьма сложным. Так, например, дробь 0,3469 писалась так: 3(1)4(2)6(3)9(4).
Виет первым стал обозначать буквами не только неизвестные, но и данные величины. Тем самым он внедрил в науку великую мысль о возможности выполнять алгебраические преобразования над символами, т.е. ввести понятие математической формулы.
Франсуа Виет, вычисляя периметры вписанного и описанного 322 216–угольников, получил 9 точных десятичных знаков.
Впервые обозначать десятичные дроби с помощью запятой предложил Франсуа Виет. До него изображение дробей было весьма сложным. Так, например, дробь 0,3469 писалась так: 3(1)4(2)6(3)9(4).
Виет первым стал обозначать буквами не только неизвестные, но и данные величины. Тем самым он внедрил в науку великую мысль о возможности выполнять алгебраические преобразования над символами, т.е. ввести понятие математической формулы
Ученый мог работать по трое суток без сна!
Теорему Виета можно обобщить на многочлены любой степени.
Непосредственно применение трудов Виета очень затруднялось тяжелым и громоздким изложением. Из-за этого они полностью не изданы до сих пор.
Г.Г. Цейтен отмечал, что чтение работ Виета затрудняется несколько изысканной формой, в которой повсюду сквозит его большая эрудиция, и большим количеством изобретенных им и совершенно не привившихся греческих терминов. Потому влияние его, столь значительное по отношению ко всей последующей математике, распространялось сравнительно медленно.
Виет первым стал применять скобки, которые, правда, у него имели вид не скобок, а черты над многочленом.
Главные открытия Ф. Виета изложены в знаменитом «Введении в аналитическое искусство», опубликованном в 1591 году. Основной замысел ученого замечательно удался: началось преобразование алгебры в мощное математическое исчисление. Франсуа называл алгебру аналитическим искусством. Он писал в письме к де Партене: «Все математики знали, что под алгеброй скрыты несравненные сокровища, но не умели их найти…»
Теорема: Знаменитая теорема, устанавливающая связь коэффициентов многочлена с его корнями, была обнародована в 1591 году. Теперь она носит имя Виета, а сам автор формулировал ее так:
«Если В+D, умноженное на А, минус А в квадрате равно ВD, то А равно В и равно D».
(B+D)·A–A =BD.
Это выражение можно переписать в привычном для нас виде:
A– (B+D)·A+BD= 0
Во время затяжной войны между Францией и Испанией, испанские инквизиторы, воюя против протестантской церкви, использовали шпионскую связь. Они считали, что придуманный ими шифр для шпионских донесений, состоящий из 600 знаков не доступен для разгадывания. Но вдруг инквизиторы узнали, что шифр расшифрован и в этом причина их неудач. Разгадал тайну шифра Франсуа Виет. Испанские инквизиторы заявили о том, что простой человек не мог разгадать шифр, обвинили Виета в заговоре с нечистой силой, которая якобы помогла ему. Заочно Виет был приговорен к смерти. Возможно, что приговор и был со временем исполнен.
Практическая часть
1. x + px – 35= 0
x1 = 7.
Найти: x2; р.
Решение:
x1 + x2 = –р
x1 · x2 = –35
7 + x2 = –p
7 · x2 = –35
7 + x2 = –p
x2 = –5
7 + (–5) = –р
x2 = –5
p = 2
x2 = –5
Ответ: р = 2; x2 = –5.
2. x – 13x + q = 0
х1 = 12, 5
Найти: x2; q.
Решение:
x1 + x2 = 13
х1 · x2 = q
12,5 + x2 = 13 (1)
12,5 · x2 = q (2)
12,5 + х2 = 13
х2 = 0,5
(2) 12,5 · 0,5 = 6,25
Ответ: х2 = 0,5; q = 0,25.
3. Составить квадратное уравнение с заданными корнями:
x1 = –7
x2 = –2
Решение:
x1 + x2 = –B
x1 · x2 = c
–7 + (–2) = –B
–7 · (–2) = c
–B = –9
c = 14
B = 9
c = 14
Ответ: x+ 9x + 14 = 0.
4. А) x + 16x + 63 = 0
D>0
Решение:
По формулам Виета:
х1 + х2 = –16
х1 · х2 = 63
х1 = –7
х2 = –9
Ответ: –7; –9.
Б) х + 2х – 48 = 0
D>0
Решение:
По формулам Виета:
х1 + х2 = –2
х1 · х2 = –48
х1 = –8
х2 = 6
Ответ: –8; 2.
5. Разность корней квадратного уравнения х + х + с = 0 равна 6. Найдите с.
Решение:
х1, х2 – корни данного уравнения.
Х1 – х2 = 6 (по условию)
х1 + х2 = –1 (по формуле Виета)
2х1 = 5
2х2 = –7
х1 = 2,5
х2 = –3,5
с = х1 · х2 = –8,75
Ответ: –8,75.
Самостоятельная работа
1. Найдите сумму корней квадратного уравнения:
.
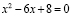2. Найдите произведение корней квадратного уравнения:
.
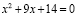3. Найдите корни неприведённого квадратного уравнения
.
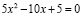4. Составить квадратное уравнение с целыми коэффициентами, корнем которого является число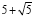 
1. Сумма корней равна 6
2. Произведение корней равно 14
3. 
.
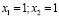4. 
.
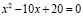Гипотеза. Применение теоремы Виета к уравнениям высших степеней
Если с помощью формул Виета можно быстро находить корни квадратного уравнения, то можно ли применить формулы к уравнениям высших степеней?
Если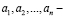 
корни многочлена
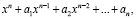
то коэффициенты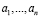 
выражаются в виде симметрических многочленов от корней, а именно:
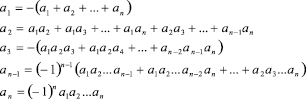
Если старший коэффициент многочлена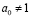 
, то для применения формул Виета нужно разделить все коэффициенты на а0.
В этом случае формулы Виета дают выражение для отношений всех коэффициентов к старшему. Из последней формулы Виета следует, что если корни многочлена целочисленные, то они являются делителями его свободного члена, который также целочисленен.
Доказательство осуществляется рассмотрением неравенства
,
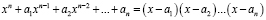где правая часть представляет собой многочлен, разложенный на множители.
Задача 2
В этом опыте я сравнила время, потраченное на решение уравнения x+3x+2=0 через дискриминант, и время на решение этого же уравнения с помощью теоремы Виета. В результате получилось, что в первом случае ученик тратит 35 секунд, а во втором – 15 секунд
Вывод: с формулами Виета можно сэкономить время.
Задача 3
Дано уравнение:
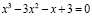
Ищем корень среди чисел: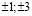 
Подбором находим один из корней уравнения, –1
Следовательно,
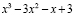
делится на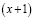 
.
Задача 4
.
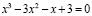По формулам Виета:
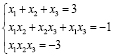
Следовательно, корни уравнения равны –1;1;3.
Вывод: формулы Виета позволяют рационально решить это уравнение.
Задача 5
При решении уравнений было замечено, что уравнения
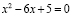
и
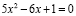
имеют взаимно обратные корни.
Гипотеза:
Корни уравнений
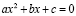
и
,
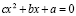где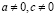 
, взаимно обратные.
По формулам Виета из первого уравнения:
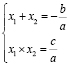
Рассмотрим числа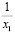 
и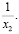 
.
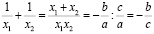
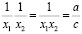Значит, эти числа являются корнями уравнения
,
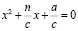что равносильно уравнению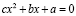 
Поскольку формулы Виета имеют обобщение для уравнения степени n , то можно быть уверенным, что утверждение об обратных корнях верно и для уравнений 3-й, 4-й и более высоких степеней.
Доказательство данного факта для уравнения 3-й степени содержится в следующей задаче.
Обратные корни.
Напишем приведённое кубическое уравнение
,
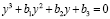корни которого обратны корням уравнения
.
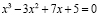Решение:
1) Пусть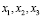 
– корни уравнения
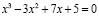
2) Т.к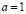 
, то по формулам Виета
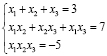
3) Пусть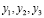 
– корни уравнения
.
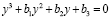4) Тогда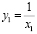 
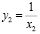
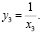
5) Т.к. a=1 , то по формулам Виета
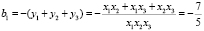
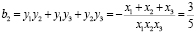
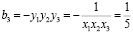
6) Следовательно искомое уравнение имеет вид:
,
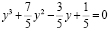или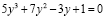 
.
Библиографическая ссылка
Керим А.Г. ФРАНСУА ВИЕТ И ЕГО ЗНАМЕНИТАЯ ТЕОРЕМА // Международный школьный научный вестник. – 2017. – № 3-3. ;URL: https://school-herald.ru/ru/article/view?id=359 (дата обращения: 28.11.2024).