Данная статья является реферативным изложением основной работы. Полный текст научной работы, приложения, иллюстрации и иные дополнительные материалы доступны на сайте III Международного конкурса научно-исследовательских и творческих работ учащихся «Старт в науке» по ссылке: https://www.school-science.ru/0317/11/28648.
Актуальность. В многочисленных войнах на протяжении всей истории человечества, враждующие стороны, доказывая своё превосходство, использовали сначала камни, копья и стрелы, а затем ядра, пули, снаряды и бомбы. Успех во многом определялся точностью попадания в цель. Однако навыка воина, разрешающей способности его глаза было недостаточно для точного попадания в цель в артиллерийской дуэли первым. Желание побеждать стимулировало появление баллистики, возникновение которой относится к 16 веку.
Довольно часто приходится иметь дело с движением тел, получивших начальную скорость не параллельно силе тяжести, а под некоторым углом к ней или к горизонту. О таком теле говорят, что оно брошено под углом к горизонту. Когда, например, спортсмен толкает ядро, метает диск или копьё, он сообщает этим предметам именно такую начальную скорость. При артиллерийской стрельбе стволам орудий придается некоторый угол возвышения, так что вылетевший снаряд тоже получает начальную скорость, направленную под углом к горизонту.
Пули, снаряды и бомбы, теннисный и футбольный мячи, и ядро легкоатлета, при полёте движутся по баллистической траектории. На уроках физкультуры мы сталкиваемся с баллистическим движением: при метании спортивных снарядов, при игре в баскетбол, футбол, волейбол, бадминтон, прыжках в длину и высоту и т.д.
Поэтому я решил более подробно изучить теорию баллистического движения, выяснить, какие параметры баллистического движения необходимо знать, чтобы увеличить точность попадания в цель.
Цель работы. Изучение баллистического движения на уроках физики у нас вызвало большой интерес. Но к сожалению эта тема в учебнике нам дана поверхностно, и мы в серьёз решили заинтересоваться ей. Мы хотим рассказать про баллистику как науку, показать баллистическое движение в практической части.
Задачи: изучить баллистическое движение; подтвердить теорию на основе эксперимента; выяснить какое значение имеет баллистика в жизни человека, изготовить модели.
Гипотеза исследования. Баллистика – раздел механики, изучающий движение тел в поле тяжести Земли. Пули, снаряды, мячи все двигаются по баллистическим траекториям.
Каким же образом при движении пули, снаряда, мяча, при прыжке с трамплина можно точно попасть в цель.
В ходе работы использовались следующие методы исследования:
• Теоретические (изучение, анализ, обобщение литературы).
• Эмпирические (наблюдения, измерения).
• Практический (эксперимент, изготовление прибора).
• Интерпретационные (количественная и качественная обработка результатов).
Практическая значимость: Изучение баллистического движения имеет большое практическое значение:
• в спорте: для вратаря, выбивающего мяч от ворот, при метании гранаты, прыжки в высоту и длину, прыжки с трамплина;
• для пожарного направляющего струю воды на крышу дома;
• для военных:при запуске баллистических ракет, мин, снарядов, пуль.
Используя законы кинематики, установленные Галилео Галилеем можно определить дальность и высоту полёта, время движения и угол наклона к горизонту.
Теоретическая часть
Понятие – баллистики
Баллистика (от греч. “ballo” – бросать, метать) – наука о движении тел, брошенных в пространстве, основанная на математике и физике. Она занимается, главным образом, исследованием движения снарядов, выпущенных из огнестрельного оружия, ракетных снарядов и баллистических ракет.
История возникновения баллистики
В многочисленных войнах на протяжении всей истории человечества враждующие стороны, доказывая своё превосходство, использовали сначала камни, копья , и стрелы, а затем ядра, пули, снаряды, и бомбы. Успех сражения во многом определялся точностью попадания в цель. При этом точный бросок камня, поражение противника летящим копьём или стрелой фиксировались воином визуально. Это позволяло при соответствующей тренировке повторять свой успех в следующем сражении.
Значительно возросшая с развитием техники скорость и дальность полёта снарядов и пуль сделали возможным дистанционные сражения. Однако навыка воина, разрешающей способности его глаза было недостаточно для точного попадания в цель. Поэтому возникла необходимость в создании науки, которая занималась бы изучением движения снарядов, копий и т.п. Мерсенн (французский математик,физик) в 1644 г. предложил назвать науку о движении снаряда – баллистикой.
Основные разделы баллистики: внутренняя баллистика и внешняя баллистика. Внешняя баллистика изучает движение снарядов, мин, пуль, неуправляемых ракет и др. после прекращения их силового взаимодействия со стволом оружия (пусковой установкой), а также факторы, влияющие на это движение. Основные разделы внешней баллистики: изучение сил и моментов, действующих на снаряд в полёте; изучение движения центра масс снаряда для расчета элементов траектории, а также движение снаряда относительно центра масс с целью определения его устойчивости и характеристик рассеивания. Разделами внешней баллистики являются также теория поправок, разработка методов получения данных для составления таблиц стрельбы и внешне баллистическое проектирование. Движение снарядов в особых случаях изучается специальными разделами внешней баллистики: авиационной баллистикой, подводной баллистикой и др.
Внутренняя баллистика изучает движение снарядов, мин, пуль и др. в канале ствола оружия под действием пороховых газов, а также другие процессы, происходящие при выстреле в канале или камере пороховой ракеты. Основные разделы внутренней баллистики: пиростатика, изучающая закономерности горения пороха и газообразования в постоянном объёме; пиродинамика, исследующая процессы в канале ствола при выстреле и устанавливающая связь между ними, конструктивными характеристиками канала ствола и условиями заряжания; баллистическое проектирование орудий, ракет, стрелкового оружия.
Баллистика – прежде всего военно-техническая наука, применяемая в проектировании орудий, ракетных пусковых установок и бомбардировщиков. На базе баллистических расчетов создаются авиабомбы, артиллерийские и ракетные снаряды. Не менее важную роль играет баллистика и в таких отраслях знаний, как проектирование космических кораблей и криминалистика. Научные основы баллистики были заложены в XVI веке.
Первыми объектами, которые создавались на основе строгих законов баллистики, были осадные метательные машины. Они были известны еще с античных времен и широко применялись вплоть до позднего средневековья (до изобретения пороха и огнестрельного оружия). Одна из таких машин – баллиста – была способна метать камни, бревна и другие предметы массой до 100 кг на расстояние до 400 м (а тяжелые стрелы даже на 1 км). По такому же принципу действовали арбалеты, катапульты, онагры (рис. 2) и требушет (рис. 1).

Рис. 1. Требушет

Рис. 2. Онагр
Позднее их вытеснила с поля боя артиллерия: пушки, минометы и гаубицы.
К началу ХVII века относятся работы великого учёного Галилея (1564–1642 г.) В 1638 г. он предположил, что траектория снаряда является параболой. С этого времени расчёты траекторий производились по формулам параболической теории.
Как самостоятельная, определённая область науки, баллистика получила широкое развитие с середины XIX века. Баллистика многим обязана трудам великих русских математиков Н.И. Лобачевского, П.Л. Чебышева, М.В. Остроградского, замечательным работам воспитанников Михайловской артиллерийской академии А.А. Фадеева, Н.В. Майевского, Н.А. Забудского, В.М. Трофимова, Н.Ф. Дроздоваи др.
До начала ХIХ века баллистикой занимались в различных странах лишь отдельные учёные. С созданием в России в 1820 г. Михайловского артиллерийского училища, преобразованного в 1855 г. в Михайловскую артиллерийскую академию, было положено начало русской артиллерийской школе.
В ХХ веке перед внешней баллистикой возникли новые задачи:
• сверхдальняя стрельба,
• составление точных баллистических таблиц, содержащих информацию о поправках прицела в соответствии с дистанциями до цели.
В настоящее время применение баллистики в боевых действиях предусматривает расположение системы оружия в таком месте, которое позволяло бы быстро и эффективно поразить намеченную цель с минимальным риском для обслуживающего персонала.
Доставка ракеты или снаряда к цели обычно разделяется на два этапа. На первом, тактическом, этапе выбирается боевая позиция ствольного оружия и ракет наземного базирования либо положение носителя ракет воздушного базирования. Цель должна находиться в пределах радиуса доставки боезаряда. На этапе стрельбы производится прицеливание и осуществляется стрельба. Для этого необходимо определить точные координаты цели относительно оружия – азимут, возвышение и дальность, а в случае движущейся цели – и ее будущие координаты с учетом времени полета снаряда.Перед стрельбой должны вноситься поправки на изменения начальной скорости, связанные с износом канала ствола, температурой пороха, отклонениями массы снаряда и баллистических коэффициентов, а также поправки на постоянно меняющиеся погодные условия и связанные с ними изменения плотности атмосферы, скорости и направления ветра.
С увеличением сложности и расширением круга задач современной баллистики появились новые технические средства, без которых возможности решения нынешних и будущих баллистических задач были бы сильно ограничены.
Движение тела, брошенного под углом к горизонту
Довольно часто приходится иметь дело с движением тел, получивших начальную скорость не параллельно силе тяжести, а под некоторым углом к ней (или к горизонту). О таком теле говорят, что оно брошено под углом к горизонту. Когда, например, спортсмен толкает ядро, метает диск или копьё, он сообщает этим предметам именно такую начальную скорость. При артиллерийской стрельбе стволам орудий придается некоторый угол возвышения, так что вылетевший снаряд тоже получает начальную скорость, направленную под углом к горизонту.
На снаряд, вылетевший из ствола с определенной скоростью, в полете действуют две основные силы: сила тяжести и сила сопротивления воздуха. Действие силы тяжести направлено вниз, оно заставляет пулю непрерывно снижаться. Действие силы сопротивления воздуха направлено навстречу движению пули, оно заставляет пулю непрерывно снижать скорость полета. Все это приводит к отклонению траектории вниз.
Будем считать, что силой сопротивления воздуха можно пренебречь. Как в этом случае движется тело?
На рис. 3 показан стробоскопический снимок шарика, брошенного под углом 60° к горизонту. Соединив последовательные положения шарика плавной линией, получим траекторию движения шарика. Это кривая называется параболой. О том, что тело, брошенное под углом к горизонту, движется по параболе, знал ещё Галилей. И опять только законы движения Ньютона и закон всемирного тяготения дают этому объяснение.

Рис. 3
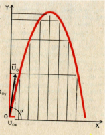
Рис. 4
Пусть из некоторой точки с начальной скоростью 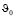 , направленной под углом ? к горизонту, брошено тело. Примем за начало отсчёта точку, из которой тело брошено. Ось X направим горизонтально, а ось Y – вертикально (рис. 4).
, направленной под углом ? к горизонту, брошено тело. Примем за начало отсчёта точку, из которой тело брошено. Ось X направим горизонтально, а ось Y – вертикально (рис. 4).
За начало отсчёта времени примем момент времени, когда тело было брошено. Из рисунка видно, что тело совершает движение одновременно вдоль оси х и оси у.
Рассмотрим движение тела вдоль оси х. Проекция начальной скорости на ось х равна
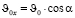 .
.
Так как на тело действует только сила тяжести, направленная по вертикали вниз, то тело движется с ускорением, которое называется ускорением свободного падения и направлено вертикально вниз. Проекция ускорение свободного падения на ось х равна нулю:
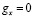 .
.
Следовательно, вдоль оси х тело движется равномерно, значит, проекция скорости на ось х в любой момент времени остаётся постоянной.
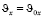 .
.
Расстояние от точки вылета тела до точки приземления называется дальностью полёта. Для расчета дальности полёта воспользуемся формулой перемещения при равномерном движении:
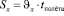 ,
,
где  – время полёта.
– время полёта.
Координата х в любой момент времени t может быть вычислена по формуле координаты равномерного движения:
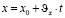 ,
,
где 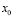 – начальная координата.
– начальная координата.
Рассмотрим теперь движение тела вдоль оси у. Проекция начальной скорости на ось у равна
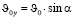
Проекция ускорения свободного падения на ось у не равна нулю:
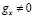 ,
,
поэтому движение тела вдоль оси у будет равноускоренным. Следовательно, проекция скорости на ось у в любой момент времени может быть вычислена по формуле
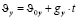 .
.
Высота подъёма тела вычисляется по формуле координаты для равноускоренного тела:
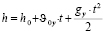 ,
,
где 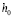 – начальная высота.
– начальная высота.
Координата у в любой момент времени вычисляется аналогично:
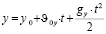 ,
,
где 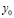 – начальная координата тела.
– начальная координата тела.
Для расчета максимальной высоты подъёма используют следующие формулы:
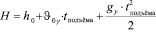 .
.
или
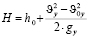 .
.
Следует помнить, что при движении тела брошенного под углом к горизонту проекция скорости на ось у изменяется и в верхней точке траектории равна нулю.
Чтобы построить траекторию, по которой движется тело, необходимо получить уравнение траектории. Для этого воспользуемся уравнениями координаты х равномерного движения и координаты у для равноускоренного движения:
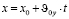 ;
;
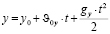 .
.
Рассмотрим движение тела из начала отсчёта, т.е.
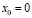 ;
; 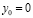 .
.
Следовательно,
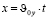 и
и 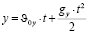
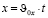
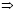
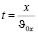 .
.
Полученное значение времени t подставим в уравнение координаты y.
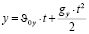 ;
;
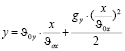 .
.
Найдём проекции на координатные оси (рис. 4):
ОХ: 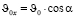
ОY: 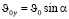 ;
; 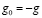 .
.
Найденные проекции подставляем в уравнение координаты у:
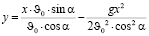 .
.
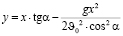 .
.
По этим формулам можно рассчитать координаты точек, которые будут изображать последовательные положения тела. Плавная кривая, проведённая через эти точки, и есть расчётная траектория. Она показана на (рис. 3). Имея эту кривую, можно узнать значение одной из координат при том или ином значении другой координаты.
Полученные результаты справедливы для идеализированного случая, когда можно пренебречь сопротивлением воздуха, температурой, ветром, влажностью и давлением воздуха, силой Кориолиса. Реальное движение тел в земной атмосфере происходит по баллистической траектории, существенно отличающейся от параболической из-за наличия условий, приведённых выше (рис. 4).
Библиографическая ссылка
Добыров И., Камашев К. ИССЛЕДОВАНИЕ БАЛЛИСТИЧЕСКОГО ДВИЖЕНИЯ // Международный школьный научный вестник. 2017. № 3-3. ;URL: https://school-herald.ru/ru/article/view?id=368 (дата обращения: 13.09.2025).
