Данная статья является реферативным изложением основной работы. Полный текст научной работы, приложения, иллюстрации и иные дополнительные материалы доступны на сайте V Международного конкурса научно-исследовательских и творческих работ учащихся «Старт в науке» по ссылке: https://school-science.ru/5/7/35910
Аннотация
В нашей жизни мы сталкиваемся с задачами, требующих нахождения оптимального решения. Некоторые из них можно решить без применения производной, а некоторые требуют нахождения максимума и минимума, наибольшего и наименьшего значения функции через производную. Задачи на оптимизацию могут быть различного содержания: алгебраического, геометрического и тригонометрического. Задачи на максимум-минимум были одними из тех, которые привели к созданию дифференциального исчисления. В процессе изучения производной в школьном курсе математики рассматриваются некоторые ее приложения в физике, а также ряд текстовых задач на нахождение наибольшего или наименьшего значений. Однако сфера производной применения этим не ограничивается. Существует масса реальных экономических задач, для решения которых необходимо использовать методы дифференциального исчисления.
Метод нахождения экстремальных значений функции имеет важнейшее, ключевое значение для решения большого класса задач из разных разделов курса физики, математики, экономики и других наук. Специфика этих задач включает получение на основе некоторых физических и математических закономерностей функциональной зависимости и нахождение экстремального значения. В наше время, в связи с научно-техническим прогрессом, в частности с быстрой эволюцией вычислительных систем, дифференциальное исчисление становится все более актуальным в решении как простых, так и сверхсложных задач.
В данной работе были рассмотрены различные задачи и приведено их подробное решение. Продуктом данного проекта является сборник, который состоит из трех частей. В первой части приведена теория по данной теме. Во второй части разобраны решения задач по блокам:
1. Задачи алгебраического содержания,
2. Задачи тригонометрического содержания.
3. Задачи геометрического содержания.
В третьей части сборника представлены подобные задачи для самостоятельного решения. В конце приведены ответы. В настоящее время подобных сборников мало и некоторые из них не имеют разнообразия в содержании или рассматриваемые задачи неактуальны в настоящее время. Так же имеются сборники, содержащие задачи либо только с применением производной, либо без ее использования: Сергей П. Актершев «Задачи на максимум и минимум» 2005 год; В. С. Михеева, О. В. Стяжкина, О. М. Шведова, Г. П. Юрлова «Математика» 2009 год; А. Ф. Бермант, И. Г. Араманович «Краткий курс математического анализа» 2010 год; И. Б. Абельсон «Максимум и минимум» 1935.
Все задачи, которые содержатся в данном сборнике, были найдены и отобраны из множества различных источников. Данный сборник поможет обучающимся старших классов более подробно изучить тему нахождения максимума и минимума, наибольшего и наименьшего значения функции и подготовиться к экзамену.
Цель: создание сборника задач на нахождения максимума и минимума, наибольшего и наименьшего значения функции различного содержания.
Для достижения поставленной цели нам необходимо решить следующие задачи:
· Изучить литературу по данной теме;
· Отобрать необходимые задачи;
· Выяснить области их применения;
· Выпустить сборник.
Методы и приемы исследования:
1. Теоретический: анализ и синтез информации при изучении литературы по теме исследования.
2. Метод обобщения полученных результатов.
Предисловие
Данный сборник «Задачи на максимум и минимум, наибольшее и наименьшее значение функции алгебраического, геометрического и тригонометрического содержания» имеет множество задач и предназначен для учащихся 10 и 11 классов.
Все задачи разбиты на три группы по теме: алгебра, геометрия, тригонометрия. При этом сборник остается пособием для самостоятельного решения задач. Сборник поделен на три главы: первая глава «Теория» содержит: понятия о максимуме и минимуме, наибольшем и наименьшем значении функции, алгоритм для решения задач на максимум и минимум, наибольшее и наименьшее значение функции, правила дифференцирования, таблица производных, а также представлен алгоритм решения задач на оптимизацию. Во второй главе «представлены решения задач различного содержания в качестве примеров для того, чтобы полностью понять тему и уметь решать по ней поставленные задачи. Третья глава «Задачи для самостоятельного решения» Третья глава предназначена для практического применения знаний полученных в предыдущих двух главах. Даны задачи, а также их ответы, по которым можно самостоятельно проверить себя.
При составлении сборника главной целью было обосновывать все решения довольно подробными объяснениями и выкладками.
Надеюсь, что данная книга окажет помощь в решении задач всем, кто будет ею пользоваться при подготовке к выпускным экзаменам в школе.
Глава 1. «Теория».

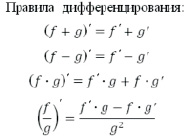
c’=0
(c·f)’= c·f’
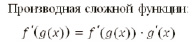
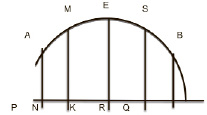
Представим себе, что путешественник, переходя через гору, прошел путь, который мы изобразили на чертеже линией AB.
Будем измерять высоту подъема от уровня моря. На чертеже уровень моря изображен прямой PQ, и если путешественник находится в точке M, то высота подъема будет представлена отрезком NM. По мере продвижения путешественника его высота над уровнем моря изменяется (т. е. является переменной величиной); пока он поднимается, эта высота увеличивается; когда он достигает вершины – точки E – высота сделается наибольшей, а затем при дальнейшем продвижении путешественника вниз по склону горы, высота путешественника над уровнем моря будет уменьшаться. Из чертежа видно, что вертикальный отрезок KE измеряющий эту высоту в точке E, будет больше, чем любой вертикальный отрезок лежащий левее KE. Когда же путешественник перейдет вершину и будет находиться правее точки E, то соответствующие вертикальные отрезки (например RS) также будут меньше чем KE. Отсюда видно, что из всех вертикальных отрезков, измеряющих высоту путешественника в различные моменты его пути, отрезок KE является наибольшим. Такое наибольшее значение переменной величины (в данном случае высоты над уровнем моря) называется максимальным.
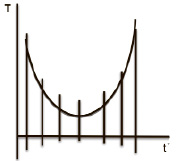
В течение летней ночи каждые 10 мин. измеряют температуру воздуха и результаты отмечают на графике. Если по горизонтальной оси откладывать время, а по вертикальной – температуру, то получим ряд отрезков (ординат).Отыскав на графике наименьшую из ординат И соответствующую ей точку 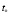 на горизонтальной оси Ot, тем самым определяем момент наиболее низкой температуры. Такое значение величины (температуры) называют минимальным; слева и справа от точки
на горизонтальной оси Ot, тем самым определяем момент наиболее низкой температуры. Такое значение величины (температуры) называют минимальным; слева и справа от точки 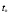 ординаты больше, чем ордината для этой точки.
ординаты больше, чем ордината для этой точки.
Общее для обоих примеров заключается в том, что переменна величина (высота, температура) в своем измерении доходит до крайнего значения – в сторону возрастания или убывания – чтобы затем начать изменения в обратном направлении. Поэтому вопросы максимума и минимума изучают параллельно. Оба эти понятия объединяют в одно понятие – крайнего или экстремального значения. Мы увидим, что задачи на максимум и минимум решаются совершенно одинаковым образом.
Определение: стационарные точки – это значения аргумента, при которых производная функции обращается в ноль.
y=3x³+2x²-7
у’= 9x2+4x
9x2+4x = 0
x(9x+4)=0
x=0 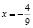
0 и 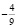 – стационарные точки
– стационарные точки
Определение: критические точки – это точки, где производная либо равна нулю, либо не существует.
Теорема 1: если f’(x)≥0, то функция f(x) возрастает . Если f’(x)≤0, то функция f(x) убывает.
Теорема 2: если функция y=f(x) имеет экстремум в точке x=x0 , то в этой точке производная функция либо равна 0, либо не существует.
Теорема 3: если f’(x) непрерывна и она имеет стационарные и критические точки, то:
4 РИСУНКА!!!!
1)
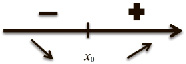
x=min
2)
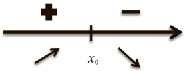
x=max
3)
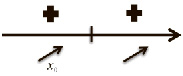
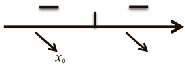
Точки экстремума нет
Алгоритм нахождения max и min
1. Найти производную f’(x);
2. Прировнять к нулю;
3. Найти стационарные и критические точки, то есть такие значения x, в которых f’(x)=0 или f’(x) не существует;
4. Нанести на числовую прямую и определить знак производной;
5. Найти max и min.
y=x3–3x2
1. f’(x)=3x2–6x;
2. f’(x)=0;
3x2–6x=0
3x(x–2)=0;
3x=0, x–2=0,
x=0, x=2
f’(–1)=3(–1)2–6(–1)=3+6+9;
f’(1)=3·12–6·1=3–6= –3;
f’(3)=3·32–6·3=27–18=9;
0 2
3. xmin=2; xmax=0/
Ответ: Возрастает на 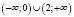
Убывает на (0;2)
Алгоритм решения задач на оптимизацию
I этап. Составление математической модели
Проанализировать условия задачи, выделить оптимизируемую величину, т.е. величину, о наибольшем или наименьшем значении которой идет речь. Обозначить ее буквой у (или S, R, V – в зависимости от содержания задачи).
Одну из участвующих в задаче неизвестных величин, через которую нетрудно выразить оптимизируемую величину, принять за независимую переменную и обозначить ее буквой х (или какой-либо другой буквой). Установить реальные границы изменения независимой переменной в соответствии с условиями задачи.
Исходя из условия задачи, выразить у через х. Математическая модель задачи представляет собой функцию у=f(х) с областью определения Х, которую нашли на втором шаге.
II этап. Работа с составленной моделью
Найти для функции у=f(х), у наименьшее или у наибольшее в зависимости от того, что требуется в условии задачи. При этом использовать теоретические установки, которые рассмотрели при определении наибольшего и наименьшего значений функции.
III этап. Ответ на вопрос задачи
Здесь следует получить конкретный ответ на вопрос задачи, опираясь на результаты, полученные на этапе работы с моделью. Записать ответ в терминах предложенной задачи.
Экономический смысл производной
Производительность труда
Пусть известна функция u=u(t), выражающая объем произведенной продукции u за время t. Тогда за время Δt=t1+t0 величина произведенной продукции составит
Δu=u(t1)– u(t0)=u(t0+Δt)– u(t0 )
Средняя производительность труда – это отношение количества произведенной продукции к затраченному времени, т.е.
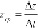
Производительностью труда в момент времени t0 называется предел, к которому стремится zср при Δt>0 :
z(t)=u’(t)
Глава 2. Задачи на максимум и минимум, наибольшее и наименьшее значение функции
2.1. Задачи на максимум и минимум, наибольшее и наименьшее значение функции алгебраического содержания
Максимум и минимум используется для решения задач, где необходимо найти наибольшее и наименьшее значение.
Задача 1. Найдите наибольшее значение функции y = x3 + 2x2 + x + 3 на отрезке [-4;-1].
Решение:
1. Находим производную f’(x)
y’ = 3x2 + 4x + 1.
2. Приравниваем к нулю
y’ = 0
3. Решаем уравнение
3x2 + 4x + 1 = 0
D = 16 - 12 = 4.
Корни 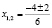 ;
;
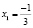 не входит в данный отрезок;
не входит в данный отрезок;
x2 = -1.
Функция непрерывна на всей области определения.
Точек, где y’ не существует, нет.
D( f ) = (-∞;+∞).
4. Наносим на числовую прямую и определяем знак производной
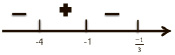
xmax= –1
Находим значения функции в этих точках и на краях отрезка. Можно увидеть, что -1 является максимальным значением, значит наибольшее значение функции в точке -1. Подставляем в функцию:
y(x) = x3 + 2x2 + x + 3;
y(−1) = (−1)3 + 2·(−1)2 − 1 + 3 = −1 + 2 −1 + 3 = 3.
Проверим остальные точки:
y(−4) = (−4)3 + 2(−4)2 − 4 + 3 = −64 +·16 − 4 + 3 = −33;
y(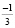 ) = (
) = (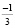 )3 + 2(
)3 + 2(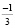 )2
)2 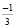 + 3 =
+ 3 = 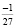 + 2
+ 2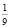
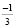 + 3 = 2
+ 3 = 2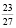 .
.
Выбираем самое большое из получившихся значений y. Это y(-1) = 3
Ответ: 3
Задача 2. Каково максимально возможное значение произведения ab если a и b – неотрицательные числа, для которых a+2b=3?
Решение:
Произведение чисел a и b максимально, когда максимально произведение чисел a и 2b – а оно максимально, когда эти числа равны, т. е. 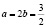 . Итак, максимальное значение произведения ab равно:
. Итак, максимальное значение произведения ab равно:

Ответ: 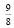
Задача 3. 1. Каково максимально возможного значение произведения двух неотрицательных чисел, сумма которых равна с? 2. Каково минимально возможное его значение?
Решение:
1. Среднее арифметическое их равно 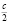 , так что их среднее геометрическое не превосходит
, так что их среднее геометрическое не превосходит 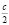 , а его квадрат (т. е. произведение чисел) не превосходит
, а его квадрат (т. е. произведение чисел) не превосходит 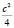 – это максимально возможное значение достигается, когда числа равны. 2. Минимально возможное значение равно 0. Так будет, если одно из чисел равно 0, а другое равно c.
– это максимально возможное значение достигается, когда числа равны. 2. Минимально возможное значение равно 0. Так будет, если одно из чисел равно 0, а другое равно c.
Ответ: 1.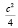 ; 2. 0
; 2. 0
Задача 4. Затраты на производство продукции объема х задаются функцией
C(x)=x2+5x=4.
Производитель реализует продукцию по цене 25 ден.ед. Найдите максимальную прибыль П. и соответствующий объем продукции x
Решение:
Записываем исходную формулу для вычисления величины, экстремальное значение которой надо найти
Прибыль равна разности между выручкой U и затратами С.
П= U – С
Находим соответствующую функцию, зависящую от х
Реализовав продукцию объема х по цене 25 ден.ед., предприниматель имеет выручку, 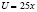 . При этом затраты составят C(x). Значит, П= U – С=25x–(x2+5x+4)=x2+20x–4.
. При этом затраты составят C(x). Значит, П= U – С=25x–(x2+5x+4)=x2+20x–4.
Определяем (по смыслу задачи) область определения функции
По смыслу задачи объем продукции х может принимать любое положительное значение, т.е. 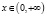 .
.
Формулируем математическую задачу
Найти наибольшее значение функции
П(x)=x2+20x–4 при 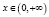
Функцию аргумента х исследуем на экстремум на найденном промежутке
П’(x)= –2x+20,
П’(x)=0,
–2x+20=0,
следовательно, стационарная точка функции x=10
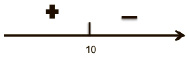
Производная меняет свой знак при переходе через эту точку с «+» на «–», значит x=10 – точка максимума.
Пmax=П(10)= –102+20·10–4=96.
Интерпретируем результаты и записываем ответ
Максимальная прибыль, равная 96 ден. ед., достигается при объеме производства 10 у.е.
Ответ: 96 ден. ед., при объеме производства 10 у.е.
Задача 5. Найдите точку максимума функции y=ln(x+4)2+2x+7.
Решение:
Заметим, что lna2=2ln(a), а значит,
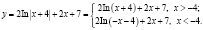
Тогда
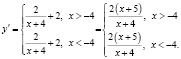
На луче 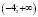 производная положительна, а функция не имеет экстремумов. На луче <<kriv035.wmf>> производная обращается в нуль в точке -5, которая является точкой максимума.
производная положительна, а функция не имеет экстремумов. На луче <<kriv035.wmf>> производная обращается в нуль в точке -5, которая является точкой максимума.
Ответ: -5
Задача 6. Найдите минимальное значение функции
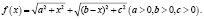
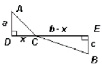
Решение:
Рассмотрим отрезок DE длины b. Восставим перпендикуляры к этому отрезку в его концах: DА = a, EВ = c (точки А и В лежат в разных полуплоскостях относительно DE, см. рис.). Пусть точка С лежит на отрезке DE и DС = x, тогда ЕС = b – x. Из прямоугольных треугольников ACD и BCE получим:
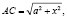
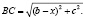
Так как АС + ВС ≥ AB, то минимальное значение данной функции равно
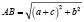
(оно достигается, когда точка C лежит на отрезке AB).
Ответ: 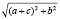 .
.
Задача 7. Дан трехчлен второй степени вида: x2+px+q (например (x2–6x+21). Найти минимальное значение трехчлена.
Решение:
Обозначим трехчлен x2–6x+21 через y, т.е. x2–6x+21=y. Если переменной x будем давать ряд значений, например x=4, x=5, x=6…, то каждому такому значению x соответствует значение y; в данном случае y=13, y=16, y=21... и т. д. Можно было бы построить большую таблицу соответствующих значений x и y и из рассмотрения ее выяснить приблизительно, при каком значении x трехчлен y=x2–6x+21 получает наименьшее значение. Но этот путь весьма длинный. Мы поступим следующим образом. Выражение x2–6x дополним до квадрата двучлена:
x2–6x=(x2–6x+9)–9=(x–3)2–9.
Тогда заданный трехчлен можно преобразовать так:
y=x2–6x+21=(x–3)2–9+21=(x–3)2+12.
В полученном выражении y=(x–3)2+12 первое слагаемое переменное (зависит от значения x), второе – постоянное. Чтобы значение y было минимальным, надо сделать первое слагаемое возможно меньшим. Теперь не трудно видеть, что из всевозможных значений x особую роль играет значение x=3; оно обращает первое слагаемое (x–3)2 в нуль. Всякое другое значение x≠3, будет ли оно больше 3 или меньше 3, сделает слагаемое (x–3)2 числом положительным, и тогда y будет больше 12. Поэтому минимальное значение трехчлена будет ymin=12, и достигается оно при x=3.
Ответ: 12.
Задачи по физике
Задача 1. Ядро выпущено из пушки, наклоненной к горизонту под углом 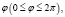 с начальной скоростью U=10 м/с2. Рассматриваем вакуум. Дальность полета ядра определяется формулой:
с начальной скоростью U=10 м/с2. Рассматриваем вакуум. Дальность полета ядра определяется формулой:
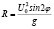 g=10 м/с2.
g=10 м/с2.
Определить угол наклона пушки, при котором дальность полета будет максимальной.
Решение:
Исходная функция: 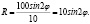
Производная заданной функции:
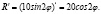
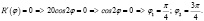
Исследуем знак 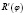 с помощью числовой прямой:
с помощью числовой прямой:
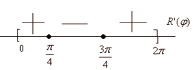
Вычислим значения заданной функции в точках 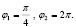
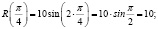
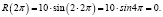
Функция достигает максимума в точке 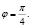
Следовательно, дальность полета ядра будет максимальной при угле наклона пушки 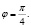
Ответ: 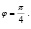
Задача 2. Шайба, скользившая по гладкому полу со скоростью vo = 12 м/с, поднимается на трамплин, верхняя часть которого горизонтальна, и соскакивает с него. При какой высоте трамплина h дальность полета шайбы S будет максимальной?
Решение:
Скорость шайбы на вершине трамплина v можно найти с помощью закона сохранения энергии:
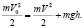
Высота трамплина и дальность полета шайбы связаны со временем полета t формулами:
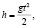 S=Vt.
S=Vt.
Из записанных выше равенств получим зависимость дальности полета шайбы от высоты трамплина:
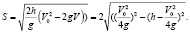
Очевидно, что дальность полета будет максимальной при условии:
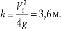
Причем сама максимальная дальность равна:
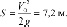
Ответ: 3,6 м.
Задача 3. Максимальная дальность полета камня, выпущенного из неподвижной катапульты, равна S = 22,5 м. Найдите максимально возможную дальность полета камня, выпущенного из этой же катапульты, установленной на платформе, которая движется горизонтально с постоянной скоростью v = 15,0 м/с. Сопротивление воздуха не учитывать, ускорение свободного падения считать g = 10,0 м/с2.
Решение:
Хорошо известно, что максимальная дальность полета тела, брошенного под углом к горизонту, достигается при угле вылета равном 45° и определяется формулой:
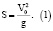
Из этой формулы можно найти скорость, которую катапульта сообщает камню:
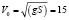 м/с.
м/с.
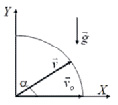
Рассмотрим теперь полет камня, выпущенного из движущейся катапульты. Введем систему координат, оси которой: X – направлена горизонтально, а Y – вертикально. Начало координат совместим с положением катапульты в момент вылета камня.
Для вычисления вектора скорости камня необходимо учесть горизонтальную скорость движения катапульты v = vo. Допустим, что катапульта выбрасывает камень под углом α к горизонту. Тогда компоненты начальной скорости камня в нашей системе координат могут быть записаны в виде:
vxo = vo + vo cos α,
vyo = vosin α. (2)
Закон движения камня имеет вид:
x = vxo = vo(1 + cos α)t,
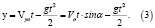
Из второго уравнения системы (3) найдем время полета, положив y = 0,

Подставив это выражение в первое уравнение системы (3), получим дальность полета камня:
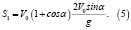
Отвлечемся немного от решения данной конкретной задачи и порассуждаем о полученном выражении.
Во-первых, если катапульта неподвижна (v = 0), то формула (5) переходит в известное выражение для дальности полета тела, брошенного с начальной скоростью под углом к горизонту:
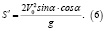
Во-вторых, из (5) совсем не следует, что S1 будет максимально при α = 45° (это справедливо для (6), когда v = 0).
Предлагая эту задачу на республиканскую олимпиаду, авторы были убеждены, что девять десятых участников получат формулу (5) и затем подставят в нее значение α = 45°. Однако, к нашему сожалению, мы ошиблись: ни один из олимпийцев не усомнился в том, что максимальная дальность полета всегда (!) достигается при угле вылета, равном 45°. Этот широко известный факт имеет ограниченные рамки применимости: он справедлив только, если:
а) не учитывать сопротивление воздуха;
б) точка вылета и точка падения находятся на одном уровне;
в) метательный снаряд неподвижен.
Вернемся к решению задачи. Итак, нам необходимо найти значение угла α, при котором S1определяемое формулой (5), максимально. Можно, конечно, найти экстремум функции, используя аппарат дифференциального исчисления: найти производную, положить ее равной нулю и, решив полученное уравнение, найти искомое значение α. Однако, учитывая, что задача была предложена ученикам 9-х классов, мы дадим ее геометрическое решение. Воспользуемся тем обстоятельством, что v = vo = 15 м/с.
Расположим векторы v и vo как показано на рисунке. Так как их длины равны, то вокруг них можно описать окружность с центром в точке О. Тогда длина отрезка AC равна vo + vocos α (это есть vxo ), а длина отрезка BC равна vo sin α (это vyo). Их произведение равно удвоенной площади треугольника АВС, или площади треугольника АВВ1.
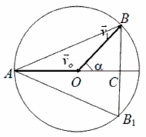
Обратите внимание, что именно произведение входит в выражение для дальности полета (5). Иными словами, дальность полета равна произведению площади ΔАВВ1 на постоянный множитель 2/g.
А теперь зададимся вопросом: какой из вписанных в данную окружность треугольников имеет максимальную площадь? Естественно, правильный! Поэтому искомое значение угла α = 60°.
Вектор AB есть вектор полной начальной скорости камня, он направлен под углом 30° к горизонту (опять же отнюдь не 45°).
Таким образом, окончательное решение задачи следует из формулы (5), в которую следует подставить α = 60°.
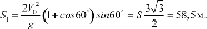
Ответ: 58,5 м.
Заключение
Было изучено большое количество литературы. Найдены и решены задачи различного содержания, используемые во многих областях науки. Данные примеры тщательно разобраны и представлены в более доступной форме. Создан сборник для самостоятельного решения, а также к каждой задаче прилагаются ответы для того, чтобы проверить себя. По представленному материалу можно целиком изучить тему, по которой написана работа.
Библиографическая ссылка
Кривошеева А.А. ЗАДАЧИ НА МАКСИМУМ И МИНИМУМ, НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЕ ФУНКЦИИ АЛГЕБРАИЧЕСКОГО, ТРИГОНОМЕТРИЧЕСКОГО И ГЕОМЕТРИЧЕСКОГО СОДЕРЖАНИЯ // Международный школьный научный вестник. – 2018. – № 5-1. ;URL: https://school-herald.ru/ru/article/view?id=640 (дата обращения: 26.04.2024).
