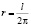Данная статья является реферативным изложением основной работы. Полный текст научной работы, приложения, иллюстрации и иные дополнительные материалы доступны на сайте VI Международного конкурса научно-исследовательских и творческих работ учащихся «Старт в науке» по ссылке: https://school-science.ru/6/7/36452.
Современное образование опирается на овладение математическими знаниями, умениями и навыками, которые будут необходимы для изучения смежных дисциплин, применения их в повседневной жизни.
Например, сосна обыкновенная – одна из ценнейших пород хвойных деревьев. Она представляет собой большой интерес не только в изучении лесных массивов в области биологии, но и является объектом для усвоения понятий и величин в математике. Поэтому использование математических основ в исследовании деревьев становится актуальным.
Целью нашей работы является описание сосны обыкновенной с помощью понятий, формул из курса математики.
В процессе исследования возникает несколько вопросов: как узнать высоту сосны, которая во много раз превышает рост человека, рассчитать массу древесины, не спиливая дерева, по состоянию хвоинок определить степень загрязнения воздуха.
Чтобы достигнуть поставленной цели и разрешить вышеперечисленные проблемы, необходимо выполнить следующие задачи:
– ознакомиться с подобранной литературой по выбранной теме;
– повторить формулы длины и площади окружности;
– найти соответствующие формулы объема ствола дерева;
– определить высоту сосны обыкновенной (несколько деревьев) и установить возраст;
– рассчитать объем и массу на корню;
– рассмотреть симметрию в строении сосны;
– изучить методику индикации чистоты атмосферы по хвое;
– оформить полученные данные в виде полигонов;
– определить возраст спиленных сосен по кольцам пней.
В ходе рассмотрения выбранного нами вопроса мы ознакомились со всевозможными способами определения высоты дерева (с помощью «высотомера», шеста, зеркала, тени, равнобедренного треугольника, фотографии, шарика, наполненного гелием, карандаша) из интернет-ресурсов и научно-популярной литературы.
Проводив исследование по данной теме, мы опирались на теоретический материал энциклопедии символов, справочника по физике и технике, методического пособия исследовательской деятельности по экологии, научно-популярной литературы, учебных пособий по школьным дисциплинам.
С различными характеристиками хвойных деревьев можно ознакомиться, прочитав статьи в интернете и книгах. Наше исследование состояло в том, чтобы на основе уже известного теоретического материала рассмотреть сосну обыкновенную на лесной территории, прилегающей к деревне, как объект для изучения математических понятий и формул. В ходе работы нами были проведены измерения высоты, длины обхвата ствола, установление возраста, вычисление радиуса, диаметра, площади поперечного сечения, объема ствола, массы на корню пяти хвойных деревьев. В результате подсчета годичных колец на пнях мы установили приблизительный возраст спиленного дерева. В процессе исследовательской деятельности рассмотрели симметрию строения сосны обыкновенной, расположение чешуек на ее шишках по спирали (ряду Фибоначчи). Изучили и применили методику индикации чистоты атмосферы по хвое. Составили и провели практические работы в 6 и 8 классах по нахождению площади поперечного сечения и определению высоты дерева; рассчитали относительную и абсолютную погрешности. Все расчеты, проводимые в работе, опирались на формулы из областей математики и физики школьного курса.
Особенно хороша была сверкающая сверху донизу королева – сосна.
М.М. Пришвин [9].
Кто-то скажет, что не видеть леса за деревьями – это плохо, а не видеть деревьев в лесу – еще хуже. Но увидеть – одно дело, а опознать его, да еще и знать про него различные факты – это уже интересно [11].
Мы привыкли понимать, что сосна является объектом изучения в науках биологии и экологии. Но мало кто задумывается над тем, что хвойное дерево имеет математические характеристики такие, как объем, высота, масса, площадь поперечного сечения, числа Фибоначчи, симметрия, относительная и абсолютная погрешность.
1. Измерение высоты и установление возраста сосны обыкновенной. Вычисление объема ствола и массы на корню дерева
«Все в природе подлежит измерению, все может быть сосчитано» – писал Н.И. Лобачевский [8].
Рассмотрим сосну обыкновенную с точки зрения математики.
1.1.Объект №1 «Сосна обыкновенная»
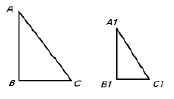
За точку отсчета выберем здание школы. Сосна (Приложение 1, фото 1) расположена на расстоянии 100 метров в юго-западном направлении. Высоту хвойного дерева мы определили по тени.
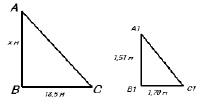
Рис. 1. Высота сосны по тени
АВ : А1В1 = ВС : В1С1 [7]
х : 1,51 = 18,5 : 1,70
1,70 · х = 1,51 · 18,5
1,70 · х = 27,935
х = 16,432
h = 16,432 м – высота сосны.
Опираясь на таблицу «Определение возраста сосны по высоте» (Приложение 2) можно сказать, что произрастание данной сосны составляет приблизительно 60 лет.
Vствола = 0,5 S1 h – объем дерева на корню;
l1 = 1,98 м – длина обхвата дерева на высоте 1,3 м;
l = 2πr – длина окружности дерева;
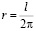 – радиус ствола;
– радиус ствола;
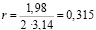 (м);
(м);
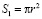 ;
;
S1 = 3,14 · 0,315 · 0,315 = 0,3115 (м²);
Vствола = 0,5 · 0,3115 · 16,432 = 2,559 (м³).
Принимая, что 1 кубический метр свежей сосновой древесины весит в среднем 650 кг [7], находим массу дерева на корню:
m = 2,559 · 650 = 1663,35 (кг) ≈ 1663 кг = 1,7 т.
2.2. Объект №2 «Сосна обыкновенная»
Сосна (Приложение 1, фото 2) находится в 300 метрах на север от школы. Высоту дерева измерили с помощью метровой линейки (h = 1,88 м). По таблице 1 Приложения 2 установили возраст (≈ 10 лет).
По формуле Симпсона:
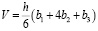 ,
,
где h – высота тела, b1 – площадь нижнего основания, b2 – площадь среднего сечения, b3 – площадь верхнего основания [7] рассчитаем объем ствола:
l1 = 0,15 м;
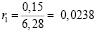 (м);
(м);
b1 = 3,14 · 0,0238² ≈ 0,0017 (м²);
l2= 0,1 м;
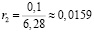 (м);
(м);
b2 = 3,14 · 0,0159² ≈ 0,0007 (м²);
l2= 0,04 м;
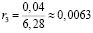 (м);
(м);
b3 = 3,14 · 0,0063² ≈ 0,0001 (м²);
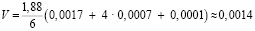 ·(м³) – объем ствола.
·(м³) – объем ствола.
Плотность сосны составляет 520 кг/м³ [3], тогда можно вычислить ее массу по формуле:
m = ρV; m = 520 · 0,0014 = 0,728 (кг) ≈ 1 кг с учетом ветвей.
2.3.Объект №3 «Сосна обыкновенная»
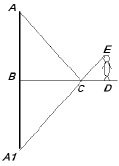
Сосна (Приложение 1, фото 3) расположена в 500 метрах на северо-восток от здания школы. Высоту хвойного дерева измерили с помощью зеркала.
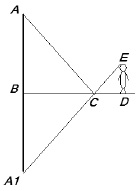
Рис. 2. Измерение высоты при помощи зеркала
Способ основан на законе отражения света. Вершина А (рис. 2) отражается в точке A1 так, что АВ = A1В. Из подобия же треугольников ВСA1 и СЕD следует, что
A1В : ЕD = ВС : СD [7]
х : 1,54 = 2,35 : 1
1 · х = 1,54 · 2,35
х = 3,619
h = 3,619 м – высота сосны; возраст приблизительно составляет 18 лет.
l1 = 0,19 м; 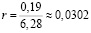 (м);
(м);
S1 = 3,14 · 0,0302² ≈ 0,0028 (м²);
V = 0,5 · 0,0028 · 3,619 ≈ 0,005 (м³) – объем ствола
Можно оценить и массу дерева на корню: m = 650 · 0,005 = 3,25 (кг).
2.4. Объект №4 «Сосна обыкновенная»
Дерево (Приложение 1, фото 4) находится в 5 метрах от объекта №3 в северо-восточном направлении. Определим высоту с помощью зеркала. Опираясь на рис. 2, ЕD = 1,54 м, ВС = 2,76 м, CD = 0,83 м, получим
A1В : ЕD = ВС : СD
х : 1,54 = 2,76 : 0,83
0,83 · х = 1,54 · 2,76
0,83 · х = 4,2504
х = 5,1209
h = 5,1209 м – высота сосны; возраст ≈ 23 года.
l1 = 0,23 м; 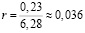 (м);
(м);
S1 = 3,14 · 0,036² ≈ 0,004 (м²);
V = 0,05 · 0,004 · 5,1209 ≈ 0,01 (м³) – объем ствола.
Масса на корню: m = 650 · 0,01 = 6,5 (кг).
2.5.Объект №5 «Сосна обыкновенная»
Сосна (Приложение 1, фото 5) расположена в 18 метрах на юг от объекта №3. Вычислим высоту дерева с помощью зеркала. С помощью рис. 2 iD = 1,54 м, ВС = 2,22 м, СD = 0,97 м имеем
A1В : ЕD = ВС : СD
х : 1,54 = 2,22 : 0,97
0,97 · х = 1,54 · 2,22
0,97 · х = 3,4188
х = 3,5245
h = 3,5245 м – высота сосны; возраст ≈ 18 лет.
l1 = 0,17 м; r = 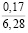 ≈ 0,027 (м);
≈ 0,027 (м);
S1 = 3,14 · 0,027²≈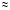 0,0022 (м²);
0,0022 (м²);
V = 0,5 · 0,0022 · 3,5245 ≈ 0,0038 (м³) – объем ствола.
Масса на корню: m = 650 · 0,0038 = 2,47 (кг).
2/6. Наглядное представление математических характеристик хвойного дерева
Данные, полученные в ходе расчетов в пунктах 1–5 § 1, представлены на полигонах (Приложение 2, рис. 3, 4, 5).
По полигонам можно установить следующие закономерности:
– чем выше хвойное дерево, тем больше у него объем ствола;
– чем больше объем хвойного дерева, тем оно тяжелее по массе;
– чем старше сосна, тем больше ее высота.
2. Биоиндикация загрязнения воздуха по состоянию сосны обыкновенной
В незагрязненных лесных экосистемах основная масса хвои сосны здорова, не имеет повреждений, и лишь малая часть хвоинок имеет светло-зеленые пятна и некротические точки микроскопических размеров, равномерно рассеянные по всей поверхности. В загрязненной атмосфере появляются повреждения и снижается продолжительность жизни сосны.
Методика индикации чистоты атмосферы по хвое сосны состоит в следующем. С боковых побегов в средней части кроны нескольких деревьев сосны в 15–20 летнем возрасте отбирают 200–300 пар хвоинок второго и третьего года жизни.
Вся хвоя делится на три части (неповрежденная хвоя, хвоя с пятнами и хвоя с признаками усыхания) и подсчитывается количество хвоинок в каждой группе [1].
Для установления загрязнения воздуха по вышеописанной методике по возрасту подходят сосны обыкновенные под номерами 3, 4, 5.
|
Повреждение и усыхание хвоинок |
Номера ключевых объектов |
|||||
|
№3 |
№4 |
№5 |
||||
|
Общее число обследуемых хвоинок |
250 |
250 |
250 |
250 |
250 |
250 |
|
Количество хвоинок с пятнами |
0 |
0 |
0 |
1 |
2 |
2 |
|
Процент хвоинок с пятнами |
0 |
0 |
0 |
0,4 |
0,8 |
0,8 |
|
Количество хвоинок с усыханием |
1 |
3 |
2 |
1 |
2 |
3 |
|
Процент хвоинок с усыханием |
0,4 |
1,2 |
0,8 |
0,4 |
0,8 |
1,2 |
|
Дата отбора проб |
24.07.2017 |
03.08.2018 |
24.07.2017 |
03.08.2018 |
24.07.2017 |
03.08.2018 |
По полученным данным таблицы мы видим, что количество хвоинок с пятнами и с усыханием ничтожно мало. Большая часть массы хвои сосны здорова. Она почти не имеет повреждений, и лишь на нескольких хвоинкам можно наблюдать некротические точки. Лесная экосистема, в которой произрастают сосны обыкновенные, не подвержена загрязнению воздуха.
3.Симметрия в строении сосны обыкновенной
В строении хвойного дерева рассматривается симметрия, которая связана с борьбой за свет, физической устойчивостью к полеганию (закон всемирного тяготения). Например, конусообразная крона сосны обыкновенной имеет строго вертикальную ось симметрии – вертикальный ствол, утолщенный книзу для устойчивости. Отдельные ветви симметрично расположены по отношению к стволу, а форма конуса способствует рациональному использованию кроной светового потока солнечной энергии, увеличивает устойчивость. Таким образом, благодаря притяжению и законам естественного отбора сосна выглядит эстетически красиво и «построена» рационально [5].
4.Определение возраста дерева по количеству колец на пне
Все слои клеток древесины, образовавшиеся весной, летом и осенью, составляют годичное кольцо прироста. Мелкие осенние клетки отличаются от крупных весенних клеток древесины следующего года, находящихся рядом с ними. Поэтому граница между соседними годичными кольцами на поперечном срезе древесины у многих деревьев хорошо заметна [6]. Подсчитав с помощью лупы число годичных колец, мы определили возраст спиленного дерева и полученные данные занесли в таблицу.
|
№ п/п |
Наименование и номер объекта |
Возраст спиленной сосны |
|
1 |
Пень. Фото 7 (Приложение 1) |
≈ 34 года |
|
2 |
Пень. Фото 8 (Приложение 1) |
≈ 31 год |
|
3 |
Пень. Фото 9 (Приложение 1) |
≈ 48 лет |
5. Числа Фибоначчи в расположении чешуек сосновых шишек
В сосновых шишках можно обнаружить спирали. Если поставить открытую ладонь вертикально перед собой, направив большой палец к лицу, и, начиная с мизинца, последовательно сжимать пальцы в кулак, получается движение, которое есть спираль Фибоначчи.
На сосновой шишке видна двойная спираль: первая спираль идет в одну сторону, вторая – в другую. Если подсчитать число шишек в спирали, вращающейся в одном направлении, и число чешуек в другой спирали, то можно увидеть, что это всегда два последовательных числа из ряда Фибоначчи [10].
Занесем результаты по подсчету чешуек сосновых шишек в таблицу.
|
№ п/п |
Наименование и номер объекта |
Числа Фибоначчи |
|
1 |
Сосновая шишка. Фото 10 (Приложение 1) |
В одном направлении – 5 и 8 чешуек, в другом направлении – 8 и 13 чешуек и т.д. |
|
2 |
Сосновая шишка. Фото 11 (Приложение 1) |
В одном направлении – 7 и 11 чешуек, в другом направлении – 11 и 18 чешуек и т.д. |
|
3 |
Сосновая шишка. Фото 12 (Приложение 1) |
В одном направлении – 7 и 9 чешуек, в другом направлении – 9 и 16 чешуек и т.д. |
6. Практическое применение
Предлагаем несколько видов практических работ по измерению и нахождению математических характеристик сосны обыкновенной.
Практическая работа №1 по теме «Длина отрезка. Единицы измерения длины. Десятичные дроби», выполненная учащимися 5 класса
Цель: определить ширину и высоту сосновой шишки в мм, перевести одни единицы измерения в другие.
Оборудование: сосновая шишка, линейка.
Сосновая шишка
|
№ п/п |
Ф.И. учащегося |
Ширина, мм |
Ширина, см |
Ширина, дм |
Высота, мм |
Высота, см |
Высота, дм |
|
1 |
… |
42 |
4,2 |
0,42 |
47 |
4,7 |
0,47 |
|
2 |
… |
43 |
4,3 |
0,43 |
42 |
4,2 |
0,42 |
|
3 |
… |
26 |
2,6 |
0,26 |
27 |
2,7 |
0,27 |
|
4 |
… |
41 |
4,1 |
0,41 |
45 |
4,5 |
0,45 |
|
5 |
… |
40 |
4 |
0,4 |
40 |
4 |
0,4 |
Практическая работа №2 по теме «Среднее арифметическое», выполненная учащимися 5 класса
Оборудование: хвоинки, линейка.
Цель: измерить длину 5 хвоинок и рассчитать среднее арифметическое.
|
№ п/п |
Ф.И. учащегося |
Длина хвоинки 1 |
Длина хвоинки 2 |
Длина хвоинки 3 |
Длина хвоинки 4 |
Длина хвоинки 5 |
Среднее арифметическое |
|
1 |
… |
45 |
46 |
40 |
43 |
47 |
44,2 |
|
2 |
… |
46 |
48 |
50 |
54 |
45 |
48,6 |
|
3 |
… |
47 |
45 |
44 |
45 |
50 |
46,2 |
|
4 |
… |
51 |
49 |
42 |
47 |
43 |
46,4 |
|
5 |
… |
52 |
49 |
50 |
47 |
48 |
49,2 |
|
Среднее арифметическое: |
46,92 |
||||||
Практическая работа №3 по теме «Определение обхвата, диаметра, радиуса и площади поперечного сечения ствола сосны», выполненная учащимися 6 класса
Цель: измерить длину обхвата сосны обыкновенной на высоте 1,3 м и рассчитать площадь поперечного сечения.
Оборудование: рулетка, метровая линейка, бечевка.
|
№ п/п |
Ф.И. обучающихся |
Обхват (длина окружности) ствола сосны, l (*) |
Радиус сосны
|
Диаметр сосны d = 2r |
Площадь поперечного сечения ствола сосны, м² |
|||
|
см |
м |
см |
м |
см |
м |
|||
|
1 |
… |
84,78 |
0,8478 |
13,5 |
0,135 |
27 |
0,27 |
0,0572265 |
|
2 |
… |
56,52 |
0,5652 |
9 |
0,09 |
18 |
0,18 |
0,025434 |
|
3 |
… |
103,62 |
1,0362 |
16,5 |
0,165 |
33 |
0,33 |
0,0854865 |
|
4 |
… |
37,68 |
0,3768 |
6 |
0,06 |
12 |
0,12 |
0,011304 |
|
5 |
… |
65,94 |
0,6594 |
10,5 |
0,105 |
21 |
0,21 |
0,0346185 |
π≈ 3,14; S = πr2; 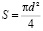
(*) – измерение обхвата ствола дерева необходимо проводить на высоте ≈1,3 м от земли.
Вывод: площадь поперечного сечения зависит от диаметра сосны. Чем больше обхват дерева, тем больше площадь поперечного сечения ствола.
Практическая работа №4 по теме «Измерение высоты одной сосны разными способами», выполненная учащимися 8 класса
Цель: найти высоту сосны обыкновенной разными способами с помощью подручных материалов.
Оборудование: рулетка, метровая линейка, бечевка, зеркало, фотоаппарат.
По полученным результатам мы рассчитаем абсолютную и относительную погрешности измерения высоты сосны обыкновенной.
|
№ п/п |
Способ измерения |
Решение |
Ответ |
|
1 |
По тени |
АВ : А1В1 = ВС : В1С1 х : 1,68 = 4,4 : 2,02 2,02 х = 4,4 · 1,68 2,02 х = 7,392 х = 7,392 : 2,02 х = 3,6594 |
3,6594 м |
|
2 |
С помощью зеркала |
Способ основан на законе отражения света. Вершина А отражается в точке A1 так, что АВ = A1В. Из подобия же треугольников ВСA1 и СЕD следует, что A1В : ЕD = ВС : СD х : 1,65 = 2,17 : 1 х · 1 = 1,65 · 2,17 х = 3,5805 |
3,5805 м |
|
3 |
По фотографии |
Возьмём фотографию, на которой изображена сосна и мерка (человек, рост которого уже известен). Найдём отношение действительного роста человека к его росту по фотографии, затем полученный результат умножить на длину сосны с фотографии (Приложение 1, фото 6). Рост ученика в действительности: 1,6 м Рост ученика на фотографии: 0,09 м Высота сосны по фотографии: 0,2 м 1,6 : 0,09 = х : 0,2 0,09 х = 1,6 · 0,2 0,09 х = 0,32 х = 0,32 : 0,09 х = 3,5555 |
3,5555 м |
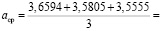
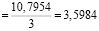 – среднее арифметическое значение измеряемой величины (высоты);
– среднее арифметическое значение измеряемой величины (высоты);
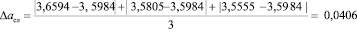 – случайная погрешность;
– случайная погрешность;
Δa= Δaсл + Δaпр [4]; Δa = 0,0406 + 0,001 = 0,0416 (м) – максимальная абсолютная погрешность; а = aср ± Δa [4]; а = 3,5984 ± 0,0416 (м).
Относительная погрешность: 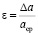 ;
; 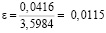 .
.
Вывод: в лесной практике такая погрешность считается вполне допустимой. С большей точностью практически невозможно измерить высоту дерева на корню. Таким образом, способы измерения высоты сосны оказываются вполне правомерными.
Заключение
С одной стороны, наша работа находит свое применение в лесной таксации. Владея математическим аппаратом, работник лесного хозяйства сможет выполнить расчеты по хвойным деревьям. Так, например, определение объемов деревьев позволяет выявлять сырьевые ресурсы, дать оценку процессов лесовыращивания, изучение толщины годичных колец помогает узнать, в каких условиях росло дерево в разные годы жизни. Лесное хозяйство проводит всесторонний учет, предусматривающий разделение леса по древесным породам, возрасту, условиям произрастания, наличию запасов древесины и другим характеризующим его показателям [8]. Таким образом, можно сказать, что выполняя вычисления по математическим формулам, мы знакомим учащихся с профессией, связанной с лесной промышленностью.
С другой стороны, мы обучаем измерять величины с помощью подручных материалов, выполнять практические работы, заниматься исследованием по предмету. Такая деятельность помогает учащимся расширять кругозор, применять полученные знания на практике и в повседневной жизни. А также, дополнительный выход в лес предоставляет возможность любоваться природой родного края.
Приложение 1
Фотографии сосны обыкновенной, пней, шишек, выполненные автором

Фото 1. (24.07.2017 г.)

Фото 2. (24.07.2017 г.)

Фото 3. (24.07.2017 г.)

Фото 4. (24.07.2017 г.)
Библиографическая ссылка
Лебедева В.Р. ПРИМЕНЕНИЕ МАТЕМАТИЧЕСКИХ ПОНЯТИЙ И ФОРМУЛ В ОПИСАНИИ СОСНЫ ОБЫКНОВЕННОЙ // Международный школьный научный вестник. 2019. № 1-3. ;URL: https://school-herald.ru/ru/article/view?id=894 (дата обращения: 21.12.2025).