Данная статья является реферативным изложением основной работы. Полный текст научной работы, приложения, иллюстрации и иные дополнительные материалы доступны на сайте VI Международного конкурса научно-исследовательских и творческих работ учащихся «Старт в науке» по ссылке: https://school-science.ru/6/7/37706.
Существуют научные знания и явления, которые привносят в обыденность нашей жизни тайну и загадку. Петля Мёбиуса относится к ним в полной мере.
У каждого из нас есть интуитивное представление о том, что такое «поверхность». Поверхность листа бумаги, поверхность стен класса, поверхность земного шара известны всем. Может ли быть что-нибудь неожиданное и даже таинственное в таком обычном понятии? Да! Это односторонняя поверхность. Пример такой поверхности – таинственный и знаменитый лист Мёбиуса.
Лента Мебиуса, которую также называют петлей, поверхностью или листом, – это объект изучения такой математической дисциплины, как топология. Топология не входит в учебную программу математики, но на мой взгляд представляет большой интерес. Поэтому я решил расширить знания по математике и поделиться ими с учащимся гимназии, на примере изучения и исследования листа Мёбиуса.
Современная математика замечательно описывает при помощи формул все ее свойства и особенности. А вот применение этой ленты в обычной жизни заставляет человека задуматься, в каких областях производства и видах деятельности она применяется. А я как житель своего города Тюмени, задумался о ее применении в нашем регионе. Оказывается, обычные люди, слабо разбирающееся в топонимике и других геометрических премудростях, практически ежедневно сталкиваются с предметами, изготовленными по ее образу и подобию, даже не подозревая об этом.
Цель моей исследовательской работы: исследовать лист Мёбиуса, его свойства, как один из объектов топологии.
Объект исследования: лента Мёбиуса.
Для достижения поставленной цели мною решались следующие задачи:
1. Найти и изучить различный материал и научную литературу о математической поверхности – лента Мёбуса. Провести анализ изученной литературы.
2. Изготовить модель, с помощью которой можно будет исследовать ленту Мебиуса, ее свойства.
3. Установить области применения ленты Мёбиуса и убедиться в том, что она нашла применение во многих привычных для нас сферах жизни.
4. Определить и представить в каких отраслях производства и видах деятельности Тюменской области она применяется.
Значимость изучения и следования моей темы заключается в том, чтобы обобщить мнения ученых, изучить разнообразные свойства и сюрпризы ленты Мёбиуса и выдвинуть свое личное отношения к данному объекту исследования. В ходе моего исследования анализируются особенности применения и необычность геометрической поверхности. Большой интерес составляет, то что у ленты Мёбиуса только одна поверхность.
Историческая справка

«Отцом» открывателем этой необычной ленты признан немецкий математик Август Фердинанд Мебиус, ученик Гаусса, написавший не одну работу по геометрии, но прославившийся преимущественно открытием односторонней поверхности в 1858 году Есть расхожее мнение, что прообразом модели «бесконечной петли» стала неверно сшитая лента служанкой профессора Августа Мебиуса.
Удивительным является тот факт, что ленту с одной поверхностью в тот же самый 1858 год открыл другой ученик Гаусса – талантливый математик Иоганн Листинг, придумавший термин «топология» и написавший серию основополагающих трудов по этому разделу математики. Однако свое название необычная лента все же получила по фамилии Мебиуса.

На самом деле, лента была открыта давным-давно еще в древнем мире. Одним из подтверждений служит находящаяся во Франции, в музее города Арль древнеримская мозаика с такой же перекрученной лентой. На ней нарисован Орфей, очаровывающий зверей звуками арфы. На фоне неоднократно изображен орнамент с перекрученной лентой.

Лист Мёбуса начало новой науки топологии
С того момента, как немецкий математик обнаружил существование удивительного одностороннего листа бумаги, начала развиваться целая новая ветвь математики, называемая топологией.
Топология это одна из разделов геометрии и является самым «молодым» из разделов современной геометрии. В ней изучаются свойства фигур и тел, которые не меняются при их непрерывных деформациях, (растяжение, сжатие), и не допускают разрывов и склеивания.
С точки зрения топологии баранка и кружка одно и то же. Сжимая и растягивая кусок резины можно перейти от одной из этих фигур к другой. А вот баранка и шар – уже будут разными объектами: чтобы сделать отверстие, надо разорвать резину.
Среди букв русского алфавита тоже есть топологически одинаковые фигуры: А-Д, Г-С, С-П, З-Э, Т-У.
Лента Мёбиуса один из объектов топологии. Удивительные свойства ленты Мёбиуса – она имеет один край, одну сторону, не связана с ее положением в пространстве, с понятием расстояния, угла и тем не менее имеют вполне геометрический характер.
Лента Мёбиуса и её свойства
Как сделать ленту Мёбиуса?
Ленту Мёбиуса очень легко сделать, подержать в руках, разрезать, поэкспериментировать как-нибудь еще. Изучение ленты Мёбиуса – хорошее введение к элементам топологии.
Лист Мёбиуса относится к числу математических неожиданностей. Чтобы изготовить лист Мёбиуса, возьмём прямоугольную полоску АВ В1А1, перекрутим её на 180 градусов и склеим противоположные стороны АВ и А1В1, т.е. так, что совместятся точки А и В1 и точки А1 и В.
Получим перекрученное кольцо. И задаемся вопросом: сколько сторон у этого куска бумаги? Две, как у любого другого? Нет. У него ОДНА сторона.

Свойства петли Мёбиуса
Ленте Мебиуса присущи следующие свойства, не меняющиеся при ее сжимании, разрезании вдоль или сминании:
1. Односторонность – топологическое свойство листа Мёбиуса, характерное только для него. Если двигаться по поверхности Ленты Мебиуса в одном направлении, не пересекая ее границ, то, в отличие от двусторонних поверхностей (например, сферы и цилиндры), попадаешь в место, перевернутое по отношению к исходному. Если двигать по этой ленте окружность, одновременно обходя ее по часовой стрелке, то в начальном положении направление обхода станет против часовой стрелки.

2. Непрерывность – это ещё одно топологическое свойство. С топологической точки зрения круг неотличим от квадрата или треугольника, потому что их легко преобразовать один в другой, не нарушая непрерывности. На листе Мёбиуса любая точка может быть соединена с любой другой точкой и при этом муравью на гравюре Эшера ни разу не придётся переползать через край “ленты”. Разрывов нет – непрерывность полная.

3. Связность, или двухмерность, заключается в том, что при разрезании ленты вдоль, из нее не получится несколько разных фигур, и она остается цельной. Чтобы разделить квадрат на две части, нам потребуется только один разрез. Но вот чтобы располовинить кольцо, потребуется уже два разреза. А лист Мебиуса? Конечно двусвязен, т. к. если разрезать его вдоль, он превратится не в два отдельных кольца, а в одну целую ленту.
Количество связей меняется в зависимости от смены количества оборотов ленты: если один оборот – двусвязен и т.д.

4. В ней отсутствует такое важное свойство, как ориентированность. Это значит, что человек, идущий по этой фигуре, вернется к началу своего пути, но только в зеркальном отражении самого себя. Таким образом, бесконечная лента Мебиуса может привести к вечному путешествию.

Таким образом, лента Мёбиуса – простейшая односторонняя поверхность с краем. Попасть из одной точки этой поверхности в любую другую можно, не пересекая края.
Ленту Мёбиуса иногда называют прародителем символа бесконечности ∞, так как находясь на поверхности ленты Мёбиуса, можно было бы идти по ней вечно. Правда, это не соответствует действительности, ведь символ ∞ использовался для обозначения бесконечности в течение двух столетий до открытия ленты Мёбиуса.
Опыты с листом Мёбиуса
Для подтверждения всех комбинаций и свойствах листа Мёбиуса я решил практически совершить ряд опытов с листом Мёбиуса, в которых постарался ответить на интересующие меня вопросы, и сделать определённые выводы.
Для проведения опытов, мы с дедушкой и папой изготовили на станке специальную модель, подобно ленте сборочного конвейера. Так же я подготовил достаточное количество бумажных лент, клей и ножницы, краски и ручка (приложение 1, 2).
Опыт № 1 (проверка свойства – односторонность)
В наше время мы привыкли встречаться с двусторонними предметами (объектами, фигурами). Изучив свойства ленты Мёбиуса и узнав, чтобы она односторонняя решил это проверить.
С помощью разработанного и изготовленного совместно с моим дедушкой механизма, демонстрирующего «Петлю Мёбиуса», я провел опыт доказывающий, что лист (лента) Мёбиуса имеет только одну сторону.
С помощью механизма прокручиваем ленту и одновременно раскрашиваем ее поверхность.
Результат: Окрасилась вся поверхность ленту, хотя я ее не переворачивал. Опыт показал нам, что у петли Мёбиуса имеется всего лишь одна сторона, а не две (приложение 1).
Опыт № 2 (проверка свойства – непрерывность).
В центре ленты Мёбиуса я нарисовал точку. С помощью механизма прокрутил ленту, и в это же время провел непрерывную линию от точки до того момента пока не вернулся к этой же точке.
Результаты: непрерывная линия проходит по двум сторонам, заканчиваясь в начальной точке. А это значит, что поверхность листа Мёбиуса является непрерывной. См. приложение № 2
Опыт № 3 (проверка на количество краёв в листе Мёбиуса).
Закрасил непрерывной линией только один край колец как обычного кольца, так и кольца Мёбиуса.
Результаты: Обычное кольцо: один край кольца был закрашен, а второй край нет. Значит, имеет два края, так как второй остался чистым. Кольцо Мёбиуса: линия края получилась, оказалась закрашена вся. Следовательно, лист Мёбиуса имеет один край (приложение 3).
ЭТО УДИВИТЕЛЬНО: Лист Мёбиуса действительно непрерывен, односторонен и имеет один край.
Опыты с разрезанием листа Мёбиуса
Опыт № 1 (что же произойдет, если разрезать обычное кольцо и кольцо Мёбиуса?).
Разрезал данные кольца посередине.
Результаты Обычное кольцо: получилось 2 кольца с одинаковой длиной и шириной (ширина будет одинакова, только если разрезать пополам, а длина всегда остается неизменной).
Кольцо Мёбиуса: получилось одна лента с двумя полуоборотами, причем длина которой в два раза больше, а ширина в два раза уже. См. приложение № 4
Опыт № 2 (что же произойдет, если разрезать ленту, отпуская от края приблизительно на треть её ширины).
Отступил от края лентяя 1/3 её ширины и порезал по этой линии.
Результат: получаются две ленты, одна-более тонкая лента Мебиуса, другая – длинная лента с двумя полуоборотами.
См. приложение № 5
Опыт № 3 (что же произойдет, если разрезать лист (ленту) на 4 равные полоски по трем линиям).
Результат: получим две ленты с двумя полуоборотами. См. приложение № 6
Опыт № 4 (что произойдет, если разрезать лист (ленту) на 6 равных частей по 5 линиям).
Результат: получим три ленты с двумя полуоборотами завязанные в узел). См. приложение № 7
Опыт № 5 (что произойдет, если разрезать лист (ленту) с тремя полуоборотами)
Результат: получится лента завитая в узел трилистника (приложение 8).
Совершенно неожиданные вещи происходят с бумажной полоской под названием лист Мёбиуса. В дальнейшем я продолжу опыты с перекручиванием колец и двойными кольцами.
Итоги опытов с разрезанием листа Мёбиуса
|
На сколько полосок разрезан листа Мебиуса |
Что получилось при разрезании |
|
|
Большие кольца |
Маленькие кольца |
|
|
2 |
1 двухстороннее |
0 |
|
3 |
1 двухстороннее |
1 одностороннее |
|
4 |
2 |
0 |
|
5 |
2 |
1 |
|
6 |
3 |
0 |
|
7 |
3 |
1 |
|
8 |
4 |
0 |
|
9 |
4 |
1 |
|
10 |
5 |
0 |
|
n |
n:2 |
Остаток от n:2 |
На основе проведенных мной опытов можно сделать следующие выводы:
1. Лента Мёбиуса имеет только один край.
2. Имеет только одну поверхность.
3. Объекты по поверхности ленты будут двигаться бесконечно.
4. Лист Мёбиуса – топологический объект. Как и любая топологическая фигура, лента Мёбиуса не меняет своих свойств, пока ее не разрезают, не разрывают.
Применение листа Мебиуса в жизни
Научное применение
Сегодня лист Мебиуса и его свойства широко применяются в науке, служа основой для построения новых гипотез и теорий, проведения исследований и экспериментов, создания новых механизмов и устройств
Так, существует гипотеза, согласно которой Вселенная – это огромнейшая петля Мебиуса. Косвенно об этом свидетельствует и теория относительности Эйнштейна, согласно которой даже полетевший прямо корабль может вернуться в ту же временную и пространственную точку.

Другая теория рассматривает ДНК как часть поверхности Мебиуса, что объясняет сложности с прочтением и расшифровкой генетического кода. Кроме всего прочего, такая структура дает логичное объяснение биологической смерти – замкнутая на самой себе спираль приводит к самоуничтожению объекта.
По мнению физиков, многие оптические законы основываются на свойствах листа Мебиуса. Так, например, зеркальное отражение – это особый перенос во времени и человек видит перед собой своего зеркального двойника.
Лист Мёбиуса в науке и технике
Патентные службы вынуждены были познакомиться с поразительными свойствами листа Мебиуса – в разное время и в разных странах зарегистрировано немало изобретений, в основе которых лежит все та же односторонняя поверхность.
В 1923 году знаменитый американский изобретатель Ли де Форест, который придумал трехэлектродную лампу – триод, предложил записывать звук на киноленте без перемены катушек, сразу «с двух сторон». Ему выдали патент № 1442632.
Изобрели магнитофон – и сразу же нашлись сообразительные люди, которые придумали особые кассеты, где магнитная лента соединяется в кольцо и перекручивается. Ясно, что тогда можно записывать и считывать подряд с двух дорожек, не снимая кассеты с магнитофона и не меняя их местами, а значит, время непрерывного звучания увеличивается ровно вдвое. (Речь идет, разумеется, о так называемой «непрерывной ленте», то есть замкнутой в кольцо, вроде автоматических телефонных часов или милицейских лозунгов о безопасности движения, передаваемых через репродукторы патрульных машин.).
В 1969 году советский изобретатель А. Губайдуллин получил авторское свидетельство № 236278 на бесконечную шлифовальную ленту, работающую обеими своими сторонами. Он предложил натянуть сделанную из специального материала ленту Мебиуса на два вращающихся ролика и покрыть ее крупинками твердого абразива. Понятно, что такая лента служит вдвое больше обычной.
Ту же идею использовали сотрудники НИИ автоматизации черной металлургии Г. Буйный и В. Изотов в своем устройстве для магнитной дефектоскопии (им выдано авторское свидетельство № 259449).
В 1963 году патентное ведомство США зарегистровало целых два «практически геометрических» изобретения. Некто Джакобс поставил свои знания топологии на службу химчистки – он придумал самоочищающийся фильтр, который представляет собой все ту же ленту Мебиуса и беспрерывно освобождается от впитанной грязи, «работая» при этом обеими своими сторонами.
А Ричард Дэвис, физик из американской корпорации «Сандиа» в Альбукерке, изобрел электрическое сопротивление, обладающее нулевой реактивностью.
В 1969 году советский изобретатель Губайдуллин предложил бесконечную шлифовальную ленту в виде листа Мёбиуса.
В 1971 году изобретатель с Урала Чесноков П.Н. применил фильтр в виде листа Мёбиуса.
И это только ничтожная часть примеров использования этой удивительной поверхности.
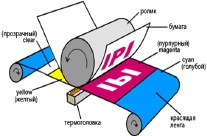
На основе исследований поверхности ленты Мебиуса и ее свойств было создано множество устройств и приборов. Ее форму повторяют при создании полосы ленточного конвейера и красящей ленты в печатных устройствах, абразивных ремней для заточки инструментов и автоматической передачи. Это позволяет значительно увеличить срок их службы, так как изнашивание происходит более равномерно.

Не так давно удивительные особенности листа Мебиуса позволили создать пружину, которая, в отличие от обычных, срабатывающих в противоположном направлении, не меняет направление срабатывания. Применяется она в стабилизаторе рулевого привода штурвала, обеспечивая возврат рулевого колеса в исходное положение.
Кроме того, знак лента Мебиуса используется в разнообразных торговых марках и логотипах. Самый известный из них – это международный символ вторичной переработки. Его проставляют на упаковках товаров либо пригодных для последующей переработки, либо сделанных из переработанных ресурсов.


Заключение
Несмотря на то, что Мёбиус сделал своё удивительное открытие очень давно, оно очень популярно и в наши дни.
Конечно же, главная ценность листа Мёбиуса состоит в том, что он дал толчок новым обширным математическим исследованиям.
Работая над проектом, я пришёл к выводу, что простая полоска бумаги, но перекрученная всего лишь раз и склеенная затем в кольцо, сразу же превращается в загадочную ленту Мёбиуса и приобретает удивительные свойства. Мной была проделана работа по доказательству некоторых свойств ленты Мебиуса. Изучались свойства ленты на наглядных примерах. В результате исследования обнаружилось, что лента Мёбиуса нашла применение во многих привычных для нас сферах жизни. Проведенные мною эксперименты подтвердили гипотезы и показали, насколько важно значение ленты Мёбиуса в жизни современного человека.
Я убеждён, что данная тема будет актуальна еще долгое время, и будут открываться все новые и новые факты, подтверждающие присутствие и влияние листа Мёбиуса на нашу жизнь.
Библиографическая ссылка
Спицын И. ЛИСТ МЕБИУСА И ЕГО ПРИМЕНЕНИЕ // Международный школьный научный вестник. 2019. № 1-3. ;URL: https://school-herald.ru/ru/article/view?id=897 (дата обращения: 04.03.2026).
