Название журнала на английском

Scientific journal ISSN 2542-0372

В последние годы значительно усилился интерес учителей общеобразовательной школы к проблеме дифференцированного подхода в обучении школьников математике на различных ступенях математического образования. Этот интерес во многом объясняется стремлением учителей так организовать учебно-воспитательный процесс, чтобы каждый ученик был оптимально занят учебно-воспитательной деятельностью на уроках и в домашней подготовке к ним с учетом его математических способностей и интеллектуального развития. Чтобы не допускать пробелов в знаниях и умениях школьников, а в конечном итоге дать полноценную базовую математическую подготовку учащимся обычного класса.

Что такое дифференциация?

Дифференциация в переводе с латинского означает разделение, расслоение целого на различные части, формы, ступени.

Дифференцированное обучение – это:

1) форма организации учебного процесса, при которой учитель работает с группой учащихся, составленной с учетом наличия у них каких-либо значимых для учебного процесса общих качеств;

2) часть общей дидактической системы, которая обеспечивает специализацию учебного процесса для различных групп обучаемых.

Дифференциация обучения (дифференцированный подход) – это:

1) создание разнообразных условий обучения для различных школ, классов, групп с целью учета особенностей их контингента;

2) комплекс методических, психологических, организационно- управленческих мероприятий.

Индивидуальный подход в учебном процессе означает действенное внимание к каждому ученику, его творческой индивидуальности, учет в процессе обучения индивидуальных особенностей, предполагает разумное сочетание фронтальных, групповых и индивидуальных заданий для повышения качества обучения и развития каждого школьника.

Цель работы учителя – обучить каждого ученика. Достичь цели «помогает дифференцированный подход к обучению, а решающую роль играет разграничение заданий по степени сложности, по степени самостоятельности учащихся при выполнении упражнений. Дифференцированный подход поможет решить многие проблемы. Главным для своей работы выделяю: обучение каждого на уровне его возможностей и способностей и приспособление (адаптация) обучения к особенностям различных групп учащихся. Я применяю в своей работе следующую гипотезу: развитие индивидуальности ребенка, его способностей, формирование личностных качеств: самостоятельности, трудолюбия и творчества.

Для того чтобы выявить ребенка с математическими способностями и делить их на группы в 7-8 классе на факультативных занятиях я и школьный психолог применяла диагностику для выявления одаренных детей, используя следующий метод Математический субтест Айзенка.

Метод Айзенка мы провели фрагментарно.

В действительности он состоит из восьми субтестов, пять из которых предназначаются для оценки уровня общего интеллектуального развития человека и три — для оценки степени развитости у него специальных способностей: математических, лингвистических и тех, которые важны для технической, дизайнерской, художественноизобразительной и других видов деятельности, где активно используется образно-логическое мышление (зрительно-пространственный субтест теста Айзенка).

Каждый из субтестов теста Айзенка включает в себя серию постепенно усложняющихся задач, на решение которых в каждом субтесте отводится по 30 мин. Таким образом, полное время работы над всем тестом, включая прохождение всех его субтестов, составляет 4 часа. Только при условии выполнения всех 8 субтестов можно дать полную оценку как уровня общего интеллектуального развития человека, так и степени развитости у него названных выше специальных способностей.

Мы воспользовались только одним субтестом Айзенка для выявления математических способностей учащихся.

На выполнение всех 25 задач дается 30 мин. Отвечать надо быстро, но обдуманно и обоснованно. Если ученик затрудняется в ответе, лучше перейти к следующей задаче. Все задачи решаемы, просто надо приложить усилия. С каждой последующей задачей материал усложняется.

Ответ на задачу состоит из одного числа. Ответ необходимо записать в бланк. Старайтесь дать как можно больше продуманных и правильных ответов, не стоит ставить числа наугад. Прежде чем приступить к решению, убедитесь, что вы верно поняли инструкцию к тестированию и то, что от вас требуется.

Оценка результатов осуществляется с помощью графика необходимо отложить на горизонтальной линии соответствующего графика количество правильно решенных задач; затем проведите вертикаль до пересечения с диагональной линией.

От точки пересечения проведите горизонтальную линию влево. Точка на вертикальной оси соответствует коэффициенту интеллекта (IQ).

С учетом диагностики и работоспособности учащихся было произведено деление на группы в 8 а классе.

На примере факультативного занятия рассмотрим как можно применить дифференцированный подход к обучению математики.

Рассмотрим с вами этап систематизации и обобщения.

На данном этапе всем группам даются задания на различных карточка вариантов:

1. Группе по теме «Уравнения, приводимые к квадратным» В данной карточке вы видите прототипы заданий входящих в ОГЭ.

Карточка №1

1)Решите уравнения

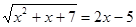
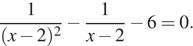
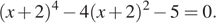
2) При каких значениях уравнение 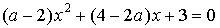имеет единственное решение?

При каких значениях 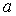уравнение 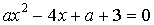имеет более одного корня?

2. Группе по теме «Квадратные уравнения», данные задания усложняется формулами сокращенного умножения и скобками и объемам заданий.

Карточка №2

1. 4x2−3x−12=3x2−6x−14

2. −3x2−x+8=(x−3)(х+3)

3. (x−9)2=−x2+15x+50

4.

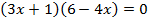
5.

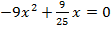
6.

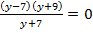
7.

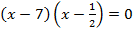
8. При каких значениях 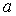уравнение 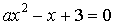имеет единственное решение?

3. Группе выдается карточка базового уровня по теме «Квадратные уравнения», с применением памятки.

Карточка №3

1.

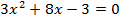
2.

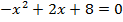
3.

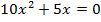
4.

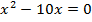
5.

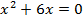
6.

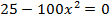
7.

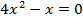
8.

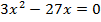
9.

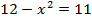
10.

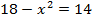
11.

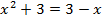
12.

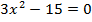
4. Группе выдается тестирование на закрепления основых понятий по теме квадратные уравнение, а также памятка с решением аналогичных заданий.

Тест “Виды квадратных уравнений”

Критерий оценивания:

Нет ошибок – 5 б.

1 – 2 ош. – 4б.

3 - 4 ош. - 3б.

5 - 6 ош. – 2б.

Более 6 ош. – 0 б.

Если в течении занятия учащиеся не справились с заданиями, то берут их на дом. На следующем занятии, осуществить проверку д/з. Кто справился с выполнением, то выдаются только ответы к карточкам. Если допущена ошибка, необходимо ее найти самостоятельно.

Прототипы данных заданий включены в ИГА как в 9 классе так в 11.