Название журнала на английском

Scientific journal ISSN 2542-0372

Геометрия является самым могущественным средством для изощрения наших умственных способностей и дает нам возможность правильно мыслить и рассуждать

Г.Галилей

Геометрия – одна из наиболее древних математических наук. Название науки «геометрия» - древнегреческого происхождения. Оно составлено из двух древнегреческих слов «гео» - Земля и «метрио» - измеряю. Геометрия основана на основе практической деятельности людей. Она непрерывно развивалась и обогащалась новыми идеями, теоремами и методами. Чуть позже геометрия сформировалась как самостоятельная наука. Но и в данное время дать точное, полное и исчерпывающее определение этой науки очень нелегко, так как интересы геометров и направление их исследований менялись в процессе исторического развития науки – геометрии.

Решение многих геометрических задач можно получить, привлекая знания из других областей наук, например, химии, алгебры, физики, географии, биологии и т.д.

В данной работе будет прослежена связь геометрии и физики, а именно барицентрический метод решения геометрических задач. В литературе встречаются и другие определения этого метода: центр масс [3, с.4], геометрия масс [4, с.16], центроид [3, с.4]. Эти «барицентрические решения» используют понятия, заимствованные из одного из раздела физики – механики: масса, материальная точка, центр масс, правило рычага [5, с.145]. Они опираются на наглядные физические рассуждения. Эти рассуждения, во-первых, дают нам решение, и, во-вторых, показывают правильный ход рассуждений. Вместе с тем «барицентрические решения» являются математически совершенно строгими. Понятие о центре тяжести стало одним из важнейших в механике и позволило сравнительно просто решать некоторые геометрические задачи. Ведь встречаются задачи, в которых дано много величин и при этом не сразу удается установить связь между ними и искомой величиной, а также грамотно обосновать ход своих мыслей. Используя данный метод или метод масс, можно существенно ускорить процесс решения задач. Несколько простых свойств центра масс позволяют решать различные геометрические задачи. В тем самым, таким путём удаётся ответить на вопросы о том, пересекаются ли несколько прямых в одной точке, принадлежат ли несколько точек одной прямой, а также находить, в каком отношении делятся отрезки.

Объект: метод геометрии масс

Предмет: геометрические задачи, решаемые с помощью барицентрического метода.

Гипотеза: может ли применение барицентрического метода значительно упростить решение многих геометрических и практических задач.

Цель исследования: познакомиться с теорией способа решения задач методом центра масс (барицентрический метод), исследование эффективности применения барицентрического метода при решении геометрических задач и применение данного метода при определении центра масс сложных геометрических фигур.

В ходе выполнения работы мной были решены следующие задачи:

1. Ознакомиться с историей открытия метода барицентра.

2. Рассмотреть основные формулировки, свойства, теоремы, связанные с данным методом.

3. Выбрать задачи из учебника Л.С.Атанасяна «Геометрия» и сайта «Сдам ГИА» и систематизировать задачи, решаемые с помощью метода геометрии масс.

4. Научиться самостоятельно решать задачи данным методом и найти барицентр города Улан-Батора.

Мной использовались следующие методы исследования:

теоретические, поисковые, сравнение, анализ.

Моя работа весьма актуальна, так как метод геометрии масс позволяет более рационально решать задачи повышенного уровня сложности с применением нестандартных, не изучаемых в школьном курсе теорем, свойств и формул. Практическая значимость данного метода состоит в том, что благодаря данному методу формируется нестандартное мышление, способствующее пониманию природы происходящих событий.

Результаты и обсуждения

1 Применение барицентрического метода (центр масс) при решении геометрических задач

Задача 1. Пусть дан треугольник АВС. ВМ – медиана, АN делит сторону ВС в отношении 1:2 от вершины В. АN пересекает ВМ в точке О. Найти отношение ВО:ОМ.

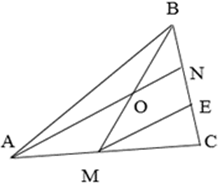1способ (Рис. 1)

Проведем ME параллельно AN.

Рассмотрим ΔANC:

AM = MC (т.к. BМ - медиана); ME║AN.

Следовательно, МЕ – средняя линия ΔANC, NE = EC.

Пусть BN = x. Тогда CN = 2x (АN делит сторону ВС в отношении 1:2). Значит, NE = EC = x. Рис. 1

Рассмотрим 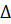ВОN и 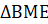: ∠МВЕ –общий, ∠ВNO = ∠BEM(АN║МЕ), следовательно, 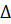ВОN 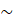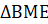( по двум углам). Из подобия треугольников следует: = = =

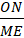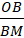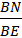Значит, BM = 2BO, следовательно,=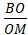

Ответ: ВО : ОМ = 1 : 1.

2 способ (Рис. 2)

Загрузим точки A, B, C соответствующими массами.

По определению центра масс для точки М:

AM × mA = MC × mC;

AM = MC (т.к. BМ - медиана),

следовательно, mA = mC = 1. Рис. 2

По определению центра масс для точки N:

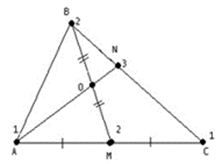
BN × mB = CN × mC; т.к. АN делит сторону ВС в отношении 1: 2 , то

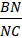= cледовательно, m = 2.

Т.к. mA = mC = 1, то mM = 2; mB = 2;

Точка О является центром масс системы двух точек В и М, значит по определению центра масс = .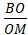

Ответ: ВО : ОМ = 1 : 1.

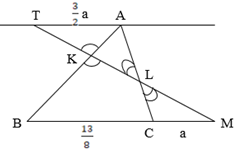Задача 2. На сторонах АВ и АС треугольника АВС отмечены точки K и L так, что AK : KB = 4:7; AL : LC = 3:2. Прямая KL пересекает продолжение стороны ВС в точке М. Найти отношение СМ:BC.

1 способ (Рис.3)

Через точку А проведем прямую ТА║ВС.

Т = ТАТМ. Обозначим СМ = a.

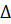ALT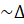CLM (по двум углам):

= = =

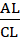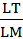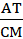AT=CM=a. Рис. 3

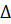AKT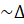BKM (по двум углам):

= = =

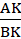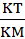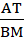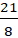BM = AT = · a = a.

Тогда BC = BM – CM = 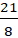a – a = 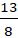a. Следовательно, СМ : ВС = 8 : 13 .

Ответ: СМ : ВС = 8 : 13 .

2 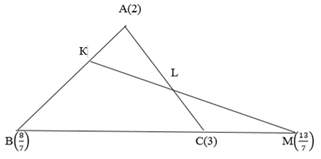способ (Рис.4)

Загрузим точки A, B, C соответствующими массами.

По определению центра масс для точки L: AL × mA = CL × mC

mA = 2; mC = 3.

По определению центра масс для точки К: Рис.4

AK × mA = BK × mB. mB =

Рассмотрим центр масс двух точек В и М: mC = mB + mM , следовательно mM = 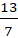, а значит СМ : ВС= 8 : 13.

Ответ: СМ : ВС = 8 : 13.

Вывод: Проведя анализ решения геометрических задач на соотношения длин отрезков, можно сделать вывод, что барицентрический метод (центр масс) наиболее рациональный и эффективный, что помогает быстро и оптимально решать задачи данного вида.

2. Определение центра масс геометрических фигур (не треугольников)

Как определить центр масс мы рассмотрели и решили геометрические задачи барицентрическим способом. Но как найти центр масс у любой геометрической фигуры? Для фигур, изучаемых на уроках геометрии, можно сделать следующие выводы:

Треугольник – центр тяжести находится в точке пересечения медиан.

Параллелограмм, ромб, квадрат, прямоугольник – центр тяжести лежит на пересечении диагоналей.

Окружность(круг) – центр тяжести лежит в центре окружности(круга).

Экспериментальным путем был найден центр тяжести у трапеции и любого четырехугольника.

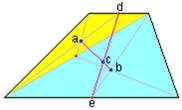Центр тяжести любого треугольника – это точка пересечения его медиан, то для нахождения центра тяжести трапеции, разобьем трапецию с помощью диагонали на два треугольника.

Получим два треугольника:

Один треугольник будем называть желтый, а другой – голубой. Рис. 5

В данных треугольниках центры тяжести лежат на пересечении медиан. В первом (желтом) треугольнике центр тяжести – а

во втором (голубом) треугольнике – b.

Центр тяжести трапеции находится в точке пересечения линии, соединяющей центры тяжести этих треугольников (отрезок ab), и средней линии трапеции, соединяющей ее основания.

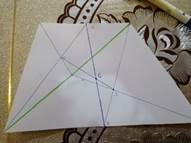
На практике я подтвердила нахождение центра тяжести трапеции.

3. Определение центра масс города Улан-Батора

Вопрос определения центра республик, областей, аймаков, городов не нова. Многие территории поставили памятники, стелы, памятные камни, обозначающие географические центры. Но совпадают ли эти географические центры с центроидом территории? Я озадачилась проблемой не только нахождения центра масс геометрических фигур, изучаемых в школе, но и более сложных фигур, которые можно разбить на геометрические фигуры, центры масс которые мне уже известны. А также определение центра города Улан- Батор. Я в своей работе попыталась найти приблизительные координаты города Улан-Батор. Положительным моментом стало – это довольно-таки ровный ландшафт.

1. Я воспользовалась схемой, которая размещена на сайте [6].

2. Увеличенное изображение города перенесла на миллиметровую бумагу, так как нужно было находить координаты точек

3. Разбила карту города на геометрические фигуры (треугольники, прямоугольники, трапеции)

4. По формулам вычислила координаты центра

5. И практическим путем проверила, что вычисленный центр совпал с центроидом сложной фигуры.

Центр города Улан-Батор находится …

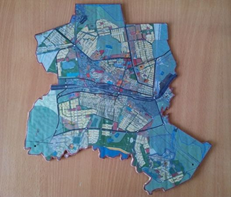
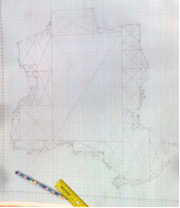
Таблица. Координаты центров и площадей геометрических фигур

Х=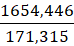= 9, 657≈ 9,7

У= 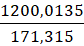= 7, 0047 ≈ 7

Центром города (барицентр) Улан-Батор является пересечение Энх тайваны оргон чолоо и Олимпийн гудамж. Но в ближайшем будущем центроид города может сместиться, так как в городе быстрыми темпами идет строительство.

Выводы

Изучив источники по этой теме убедилась в тесной связи двух предметов - математики и физики, а также я научился решать геометрические задачи на отношение длин отрезков и обращаю внимание, что данный метод позволяет более быстро решить задачу и более рационально.

В процессе исследования данной проблемы мною усовершенствовались умения и навыки работы с научно-популярной литературой, интернет-источниками.

По результатам исследований, проведённых мною, делаю следующие выводы:

с помощью исследования выяснила, что физических представлений понятия центра масс достаточно для решения целого ряда задач, изучаемых в школьном курсе математики;

определила, что область применения барицентрического метода при решении задач огромна;

исследовала применение барицентрического метода к решению геометрических задач на отношение длин отрезков;

основной результат моей работы – нахождение центра масс сложной планиметрической фигуры.

Анализируя результаты исследования, считаю, что практическая значимость моей работы заключается в следующем:

полученные дополнительные знания по данной теме укрепили мой интерес к математике;

я убедилась в рациональности применения барицентрического метода к решению задач на отношение длин отрезков, а значит цель работы достигнута.

Гипотеза подтвердилась, что данный метод значительно упростит решение многих геометрических и практических задач. Работа над темой геометрия масс (центр масс, центроид) мною не закончена, впереди поиск многих интересных задач, быстро решаемых с помощью этого метода.