Введение
Физические явления, которые изучаются в курсе астрономии, практически экспериментально не воспроизводимы. Компьютерное моделирование важным инструментом в изучении курса физики и астрономии [1]. Математическая модель физического явления является путем к пониманию различных вариантов физического взаимодействия объектов в реальном мире.
Наблюдения астрономов показывают, что в ходе эволюции звёзд происходит процесс угасания звезды. Под воздействием сил гравитации нагретый газ красных гигантов и сверхгигантов разлетается по Вселенной, образуя молодую планетарную туманность. Через сотни тысяч лет туманность рассеивается, а на её месте остаётся вырожденное ядро красного гиганта белого цвета – белый карлик. При небольших размерах остывание небесного светила происходит очень медленно. Такая судьба ожидает и звезду нашей планетарной систем - Солнце.
С этой точки зрения изучение структуры белых карликов является актуальной познавательной задачей при изучении темы «Строение и эволюция Вселенной», тема «Эволюция звезд»» в курсе астрономии.
Цель настоящего исследования – разработать компьютерную программу для изучения структуры белых карликов. Под структурой белого карлика далее будем понимать профиль плотности вещества внутри звезды и ее радиус.
Задачами исследования являются:
- Изучить теоретический материал для моделирования структуры белых карликов;
- Разработать компьютерную программу для моделирования структуры белых карликов на языке программирования Паскаль.
Гипотеза исследования. Экспериментальная возможность для изучения структуры белых карликов отсутствует. Анализ учебной литературы показывает, что поставленная цель может быть достигнута путем разработки компьютерной программы, реализующей одну из моделей для определения структуры белых карликов на основе известных законов физики.
Объектом исследования является структура белых карликов.
Предметом исследования является зависимость между массой звезды и ее радиусом — величину, которую можно определить из астрономических наблюдений.
Основная часть
Теоретическая часть. Изложению рассматриваемой темы посвящено много учебной литературы [2,3].
Белые карлики — это холодные звездные объекты, состоящие в основном из тяжелых ядер и электронов. Звезды такого типа являются одним из возможных конечных результатов течения обычных ядерных процессов, в ходе которых синтезируются элементы путем связывания нуклонов в ядра.
Предположения и допущения модели:
1. Звезда сферически-симметрична (т.е. состояние в ее любой точке зависит только от расстояния между этой точкой и центром звезды).
2. Вращение у звезды отсутствует.
3. Можно пренебречь влиянием магнитного поля.
4. Звезда находится в механическом (гидростатическом) равновесии.
5. Вещество внутри звезды рассматриваем как вырожденный газ []. Давление внутри звезды является функцией плотности (уравнение состояния).
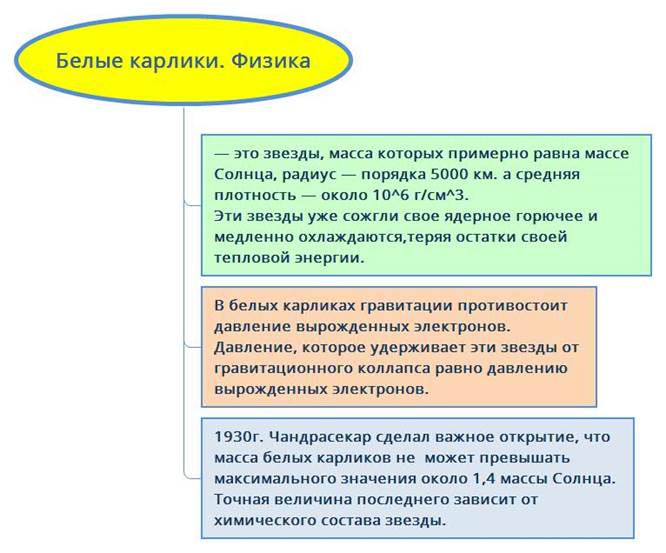
Рисунок 1. Физика белых карликов.
При выполнении условия гидростатического равновесия гравитационная сила, приложенная к некоторому объему вещества, уравновешивается перепадом давления P. Сила, связанная с перепадом давления и действующая на единицу объема, равна 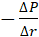 .
.
Сила тяжести, действующая на единичный объем вещества на расстоянии r от центра, равна
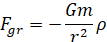
где G — гравитационная постоянная, ρ(r) — массовая плотность, а m(r) — масса звезды, заключенная внутри сферы радиуса r:
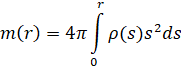
Когда звезда находится в равновесии, результирующая этих сил (гравитации и давления), приложенная к любому пробному объему вещества, должна быть равна нулю:
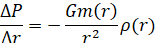
Это уравнение можно переписать в виде []:
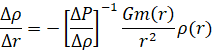
Изменение массы вдоль радиуса следует из соотношения между массой и плотностью:
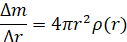
В результате получена система уравнений в конечных разностях, которые определяют структуру звезды.
Чтобы описание системы было полным, необходимо знать уравнение состояния вещества, связывающее его плотность с величиной давления, необходимого для поддержания этой плотности.
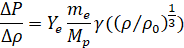
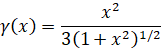
где Ye — среднее число электронов, приходящихся на одно ядро, Mp и me — масса протона и электрона соответственно, ρ0 = 9.79·105Ye−1 г· см−3.
Начальные условия задаются в виде
плотность в центре ρ(0) = ρc, масса в центре m(0) = 0.
Решение полученной системы по r в нарпавлении от центра дает профиль плотности вещества внутри звезды и ее радиус R (плотность стремиться к нулю). Масса звезды определяется как M=M(R). Поскольку M и R зависят от ρс, то, изменяя этот параметр, можно изучать структуру звезд разной массы, вычисляя кривую R=R(ρc), M =M(ρc), ρc ∈[ρA, ρB] в координатах (R, M).
Таким образом поставленная цель может быть достигнута.
Программа для решения задачи. Преобразуем систему к безразмерной форме [4]. Введем безразмерные переменные для радиуса, плотности и массы: r = R0x, ρ = ρ0y1, m = M0y2, где R0 = 7.72·108Ye см, M0 = 5.67·1033Ye2 г.
Безразмерные уравнения запишутся в виде
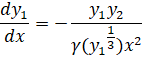
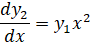
y1(0)=ρc, y2(0)=0
Ниже приведен листинг программы, реализующий данный алгоритм.
Листинг программы.
{ Структура белых карликов}
program wkmy;
Var
ro0:double; {начальная плотность в безразмерных координатах}
Ye,R,M,Ro:double;
{}
Var
y:array[1..2] of double;
x,eps,h: double;
n:integer;
{функции правой части}
function fgam(x1:double):double;
var
temp0:double;
begin
temp0:=x1**0.333333;
fgam:=x1*x1/sqrt(1+x1*x1)/3;
end;
{текущие значения правой части}
function fun(j:integer;x1:double;y1:double;y2:double):double;
var temp1:double;
begin
if j=1 then
begin
temp1:=x1*x1;
temp1:=y1*y2/temp1;
fun:=-temp1/fgam(y1);
end;
if j=2 then fun:=x1*x1*y1;
end;
Procedure rukutm;
var w,k1,k2,k3,k4:array[1..2] of double;
var j:integer;
begin
{ writeln(fun(1,x,y[1],y[2]),' ',fun(1,x,y[1],y[2]));}
for j:=1 to n do w[j]:=y[j];
for j:=1 to n do k1[j]:=h*fun(j,x,w[1],w[2]);
for j:=1 to n do y[j]:=w[j]+1/2*k1[j];
for j:=1 to n do k2[j]:=h*fun(j,x+1/2*h,w[1],w[2]);
for j:=1 to n do y[j]:=w[j]+1/2*k2[j];
for j:=1 to n do k3[j]:=h*fun(j,x+1/2*h,w[1],w[2]);
for j:=1 to n do y[j]:=w[j]+k3[j];
for j:=1 to n do k4[j]:=h*fun(j,x+h,w[1],w[2]);
for j:=1 to n do y[j]:=w[j]+(k1[j]+2*k2[j]+2*k3[j]+k4[j])/6;
x:=x+2*h;
end;
begin
ro0:=1;
n:=2;
eps:=5e-2;
h:=0.01;
y[1]:=ro0;
y[2]:=0;
x:=0.1;
writeln(' x y1 y2');
while eps<=y[1] do
{while x<=3 do}
begin
writeln(x:15:8,y[1]:15:8,y[2]:15:8);
rukutm;
end;
Writeln;
Writeln('Параметры белого карлика');
Ye:=26/56; {железо, 1/2 - углерод}
Ro:=9.79*10e5/Ye;
Ro:=Ro*y[1];
Writeln('Плотность в центре: ',Ro, ' г/см^3');
M:=5.67*10e33*Ye*Ye;
M:=M*y[2];
Writeln('Масса звезды: ',M,' г');
R:=7.72*10e8*Ye;
R:=R*x;
Writeln('Радиус звезды: ',R,' см');
end.
Результаты и обсуждение
Результат работы программы для ρс = 1 приведен ниже.
x y1 y2
0.10000000 1.00000000 0.00000000
0.12000000 1.00000000 0.00011033
0.14000000 0.99969993 0.00026667
0.16000000 0.99916126 0.00047694
0.18000000 0.99841765 0.00074904
0.20000000 0.99748917 0.00109083
0.22000000 0.99638865 0.00151011
0.24000000 0.99512476 0.00201462
……
3.66000000 0.09418865 2.51282955
3.68000000 0.09138326 2.52548119
3.70000000 0.08862698 2.53789034
3.72000000 0.08591943 2.55005619
3.74000000 0.08326025 2.56197806
3.76000000 0.08064908 2.57365534
3.78000000 0.07808554 2.58508753
3.80000000 0.07556927 2.59627425
3.82000000 0.07309989 2.60721519
3.84000000 0.07067704 2.61791017
3.86000000 0.06830032 2.62835909
3.88000000 0.06596937 2.63856195
3.90000000 0.06368380 2.64851886
3.92000000 0.06144325 2.65823002
3.94000000 0.05924733 2.66769574
3.96000000 0.05709566 2.67691643
3.98000000 0.05498787 2.68589257
4.00000000 0.05292359 2.69462477
4.02000000 0.05090243 2.70311373
Параметры белого карлика
Плотность в центре: 1031619.76482127 г/см^3
Масса звезды: 3.31391164660365E+34 г
Радиус звезды: 14480514285.7143 см
Для некоторых случаев уравнения состояния рассматриваемая система имеет аналитическое решение (вырожденный электронный газ в релятивистском приближении) [3]:
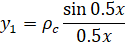
При ρc = 1 значение функции y1 будет равно 0 при x = 2π, что подтверждает выполнение программы, как показано ниже
x y1 y2
0.10000000 1.00000000 0.00000000
0.12000000 1.00000000 0.00011033
0.14000000 0.99992927 0.00026667
0.16000000 0.99980229 0.00047699
0.18000000 0.99962693 0.00074926
……
6.08000000 0.03479487 12.70208708
6.10000000 0.03136440 12.71497066
6.12000000 0.02795291 12.72666050
6.14000000 0.02456054 12.73714721
6.16000000 0.02118745 12.74642152
6.18000000 0.01783376 12.75447428
6.20000000 0.01449962 12.76129645
6.22000000 0.01118517 12.76687910
6.24000000 0.00789055 12.77121343
6.26000000 0.00461588 12.77429074
6.28000000 0.00136130 12.77610249
Параметры белого карлика
Плотность в центре: -39495.6798266984 г/см^3
Масса звезды: 1.56160203476767E+35 г
Радиус звезды: 22580999999.9998 см
Использование настоящей программы позволяет строить профили плотности вещества внутри звезды и ее радиуса при различных начальных условиях.
Выводы
В статье представлена физическая модель белых карликов и предложена программа моделирования их структуры. Приведен текст программы для решения поставленной задачи.
При использовании предлагаемой программы обучающиеся могут произвести расчет профиля плотности вещества внутри звезды и ее радиуса при различных начальных условиях.
Работа способствует междисциплинарным связям предметов, изучаемых на предметах естественнонаучного цикла среднего профессионального образования.
