I. ВВЕДЕНИЕ
В нашем мире еще много неразгаданных тайн, некоторые из них ученые уже смогли определить и описать.Числа Фибоначчи и золотое сечениеявляются основой разгадки окружающего мира и построения его формы. Эти числа подчинены единым законам природы и имеют большой практический и теоретический интерес во многих науках.
Последовательность чисел Фибоначчи — один из классических примеров рекурсии в математике. Рекурсивные алгоритмы используются в программировании для упрощения вычислений. Умение обращаться с ними является одним из базовых навыков программиста. Поэтому расчет числа Фибоначчи часто является тестовым заданием, которое дается соискателю на вакансию программиста для проверки его навыков или применяется в обучении будущих кодеров. Поэтому данная тема меня интересует с точки зрения моего профессионального будущего.
Участвуя в разнообразных олимпиадах по программированию мне встречаются задачи на вычисление ряда Фибоначчиили N-го числа в последовательности Фибоначчи. Учитывая, что время на нахождение ответа часто ограничено 1-5 секундами, передо мной встала задача найти наиболее эффективный метод решения поставленной задачи за минимальный промежуток времени.
Цель: на основе компьютерного эксперимента определить наиболее эффективный метод вычисления n-го числа Фибоначчи.
Гипотеза проекта: наиболее эффективным, из описываемых в проекте методов нахождения n-го числа Фибоначчи, является матричный метод.
Задачи:
1) изучить известные методы нахождения n-го числа Фибоначчи или разработать их самостоятельно;
2) отобрать методы решения поставленной задачи и написать функцию на языке программирования JavaScript для каждого из них;
3) оценить эффективность каждого метода на скорость и точность результата;
4) оформить выводы по итогам экспериментальной деятельности;
5) представить результаты работ в виде готового протестированного программного кода.
Методы исследования: сбор теоретической информации в справочной, научной литературе, материалах сети Internet; анализ, синтез, наблюдение, индукция и дедукция; формализация, моделирование, компьютерный эксперимент на основе программирования, который включает в себя создание определенных условий, отладку, тестирование, наблюдение за происходящим и фиксацию результатов.
Актуальность:
В компьютерную эру золотое сечение (золотая спираль) и числа Фибоначчи нашли свое применение в визуальном искусстве, 2D/3D-моделировании и веб-дизайне.
Решетка Фибоначчи применяется для эффективного наложения точек на двухмерные и трехмерные объекты, например сферу или многогранники. Таким способом можно выполнить высокоточную огранку ювелирных камней или построить визуальную модель молекулярных решеток некоторых веществ.
На основе числовой последовательности Фибоначчи строится один из вариантов фракталов — самоподобных фигур. Эту математическую модель можно использовать в компьютерной графике для построения ветвящихся объектов (ветвей, корней деревьев, русел рек, кристаллов и т. д.).
Золотое сечение применяется в веб-дизайне для разметки страниц некоторых сайтов или веб-приложений. Элементы интерфейса, организованные таким способом, образуют визуально привлекательную и удобную рабочую область [4].
Практическое применение эти числа нашли в трейдинге: коррекции, дуги, веера, временные зоны Фибоначчи. Хотя цикличность рынка и фондовых показателей действительно существует, на нее влияет множество факторов, которые невозможно предугадать строгими математическими законами. Тем не менее, в ситуации минимального внешнего влияния использование биржевых инструментов, построенных на строках Фибоначчи, действительно позволяет с определенной эффективностью прогнозировать поведение цен, индексов акций.[7]
Данный проект может представлять теоретический и практический интересы для лиц: изучающим программирование наJavaScript, занимающимся изучением свойств чисел Фибоначчи, тем, кто готовиться к олимпиадам по информатике или тем, кто хочет удачно пройти собеседование в крупную IT-компанию.
II. НАУЧНАЯ СТАТЬЯ (ТЕОРЕТИЧЕСКАЯ ЧАСТЬ)
Числа Фибоначчи - этоцелые натуральные числа, расположенные в числовой последовательности таким образом, что каждое последующее число является суммой двух предыдущих чисел, при этом в этом числовом ряде проявляются уникальные интересные свойства, выраженные в постоянных отношениях между отдельными членами последовательности и формировании некоторых постоянных коэффициентах, имеющих громадное научное и прикладное значение [3].
Изучая научную литературу и источники сети Интернет, я обнаружил несколько различных методов нахождения n-го числа Фибоначчи:
1. Рекурсия.
2. Итеративный метод.
3. Формула Бине.
4. Матричный метод.
Числа Фибоначчи – последовательность, в которой первые два члена равны нулю и единице, а каждый последующий равен сумме двух предыдущих:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, …
Ряд Фибоначчи задаётся следующей формулой:
Fn=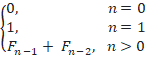 
Иногда числа Фибоначчи рассматривают и для отрицательных значенийnкак двусторонне бесконечную последовательность, удовлетворяющую тому же рекуррентному соотношению. Соответственно, члены с отрицательными индексами легко получить с помощью эквивалентной формулы «назад»:
Fn= Fn+2 - Fn +1
В ходе решения поставленных задач мы будем рассматривать нахождение чисел Фибоначчи с отрицательными индексами.
Перед началом практической части нужно так же сказать, что ряд Фибоначчи – это быстро растущая геометрическая прогрессия, и, если мы хотим работать с большими числами этой последовательности, нужно решить следующую проблему: JavaScript может корректно выполнять вычисления только с числами, входящими в диапазон от -(253-1) до 253-1,если эти числа хранятся в типе данных number, в то время как уже семьдесят девятое число Фибоначчи выходит за этот диапазон, поэтому тип данных number не подходит. Решением данной проблемы является такой специальный тип данных для работы с большими целочисленными значениями в JavaScript, как BigInt, который мы и будем использовать в дальнейшей работе.
Из-за ограничений, которые накладывает работа с BigInt, мы не можем использовать для решения поставленной задачи формулу Бине, так как в ней есть иррациональные числа.
Так же стоит отметить, что все указанные в проекте замеры времени основаны на характеристиках моего компьютера.
III. ПРАКТИЧЕСКАЯ ЧАСТЬ
3.1. Рекурсивный метод
Самое простое решение – это рекурсивный метод. Состоит в том, чтобы функция f получала на вход нужное нам число Фибоначчиn и возвращала его же в типе данных BigInt, если n=0 или n=1 (обусловлено тем, что f(0) = 0, af(1) = 1), иначе, если n>1, функция вернёт f(n-1) + f(n-2). Если же и предыдущее условие неверно, то логично следует, что функция получила n<0 и нам нужно воспользоваться формулой для отрицательных n, то есть функция будет возвращать f(n+2) -f(n+1). Получившийся код:
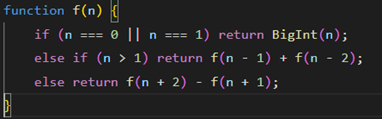
Пропишем тестирующую систему:
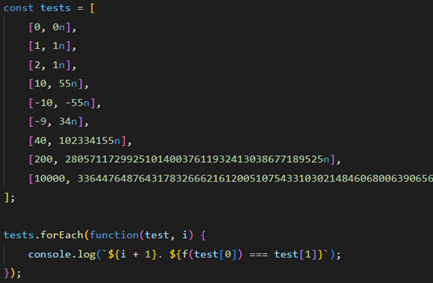
Функция успешно прошла первые 7 тестов, но время на нахождение уже 200 члена последовательности затягивалось дольше десяти минут. Испытание было признано неуспешным и прервано.
Это обусловлено тем, что одни и те же числа Фибоначчи высчитываются несколько раз, всё это наглядно показано на схеме:
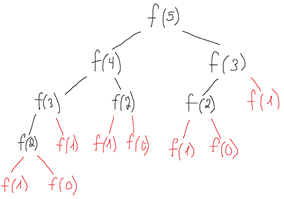
Для нахождения пятого члена последовательности Фибоначчи алгоритм дважды будет высчитывать третье число Фибоначчи, 3 раза будет высчитывать второе число Фибоначчи и так далее. Чем больше будет заданное n, тем больше будет повторных расчётов, которые замедляют работу функции.
Вывод: данный способ решения задачи является самым легким, но крайне неэффективным из-за больших затрат по времени.
3.2. Итеративный метод
В основе лежит обычный итеративный алгоритм, который будет запоминать 2 члена последовательности(условно назовём их Fnи Fn+1), на основе их высчитывать следующее член (Fn+2),передавать значение Fn+1 в переменную Fn, а значение Fn+2 в переменную Fn+1. Тело цикла будет выполняться n-2 раза, в результате будет вычислено нужное число Фибоначчи.Заметим, что такой метод подойдёт только для положительных n, для отрицательных нужно делать всё в точности наоборот.
Приступим к написанию алгоритма. Зададим переменные fnи fn1, которые будут равны 0 и 1 соответственно, а также пустую переменную fn2. Теперь создаём условие n> 0,при истинности которого начнёт свою работу цикл «for», который осуществляет обмен переменными в сторону положительного n, а при ложности начнёт работу другой цикл «for», предназначенный для отрицательных n и равного нулю .По итогам выполнения всего алгоритма мы возвращаем fn1.
Получившийся код:
|
|
По итогам запуска тестирующей системы можно сделать вывод, что алгоритм работает без ошибок, и время нахождения решения задачи меньше предыдущего зафиксированного результата.
|
У данного решения есть лишь один недостаток: если потребуется найти, к примеру, миллионный член последовательности, то по времени это займёт более 8 секунд.
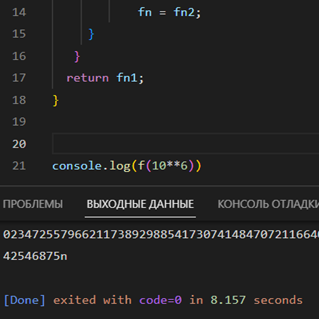
Вывод: итеративный метод позволит быстро вычислять только первые сто тысяч членов последовательности. Увеличение количества циклов может радикально увеличить длительность всего процесса.
Для уменьшения времени на нахождение числа Фибоначчи, при n>100 000 нужно найти более эффективный метод решения задачи.
2.1. Матричный методИз математических справочников можно узнать, что для любого n справедливо равенство:
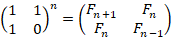
Формула означает, что квадратная матрица 2 на 2 со значениями 1, 1, 1, 0 в степени n (нужный нам номер члена в ряду Фибоначчи) будет давать новую квадратную матрицу такой же размерности со значениями Fn+1, Fn, Fn, Fn-1.
Матрица – это, прямоугольная числовая таблица, которая имеет размерность (количество строк и столбцов). Если количество строк в матрице равно количеству столбцов, то такую матрицу принято называть квадратной. Над матрицами можно проводить различные математические операции, но нас, в рамках данного проекта, интересует возведение квадратной матрицы в степень.
Возведение матрицы в степень n– это, как и если при работе с обычными числами, умножение матрицы саму на себя n количество раз. В нашем случае нужно умножать саму на себя матрицу 2 на 2. Ознакомившись с правилами произведения матриц, можно вывести формулу для нахождения произведения двух матриц такой размерности:
∙ 
= 
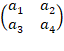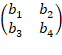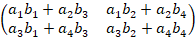(1)
Из математических справочников можно узнать, что для возведения матрицы в отрицательную степень nнужно сначала найти матрицу, обратную данной, а затем возвести её в степень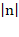 
. Ознакомившись с правилами нахождения обратной матрицы можно утверждать, что для любого отрицательного nсправедливо:
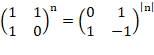
При возведении матрицы в степень 0 получается единичная матрица. Единичная матрица – это квадратная матрица, элементы главной диагонали которой равны единице, а все остальные равны нулю. В нашем случае:
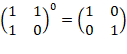
Чтобы найти самый рациональный способ возведения матрицы в степень обратимся к свойствам степеней, а именно: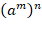
=
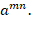То есть если мы захотим возвести условную матрицу P в степень 8 будет быстрее три раза возвести её в квадрат 
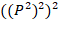, чем перемножать саму на себя 8 раз. В программном коде мы должны реализовать следующую формулу чтобы добиться максимальной скорости возведения в степень:
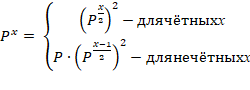(2)
Мы можем таким способом делить степень на 2 пока не получим в результате степень, равную единице, а затем, используя формулу (1),найти вторую, четвертую и т.д. степени матрицы. Реализовать такую логику в программном коде удобнее с помощью рекурсии.
Приступим к написанию функции. В самом начале зададим условие: если n = 0, то функция просто будет возвращать 0.
Далее создадим константу P,которая, в зависимости от того больше или меньше значение числа n нуля, будет равна массиву [1, 1, 1, 0]или [0, 1, 1, -1] соответственно. Для начала пропишем функцию multiply, которая принимает 2 параметра: массив B и логическую переменную equal, которая по умолчанию равна true. Создадим внутри этой функции константу A, которая, в зависимости от значения equal, будет равна либо B, если equal =true, либо – P в противном случае. По итогу функция вернёт нам матрицу, равную произведению A* B. Иными словами: если параметр equal= true, то функция multiplyпросто вернёт матрицу B2, иначе произведение матрицы P*B.
Теперь нужно написать еще одну функцию degree, которая уже и будет возводить нашу матрицу Pв степень xс помощью описанной выше формулы(2). Задаём первое условие: если x = 1, то функция просто вернёт P, иначе если остаток от деления xна 2 равен нулю (проверяем таким способом xна чётность), то функция вернёт квадрат матрицы, которую вернёт функция degree, вызванная для параметра x/2. Иначе, если xнечётный, функция вернёт нам произведение матрицы Pна квадрат матрицы, которую вернёт функция degree, вызванная для параметра (x– 1) / 2.
В конце основной функцииf нужно дописать, что она вернет элемент в массиве, который вернёт функция degree, вызванная для модуля числа n.Функция degreeвозвращает нам матрицу pn, а в такой матрице нужное нам число будет находиться в массиве по индексу 1.
|
Получившийся код: |
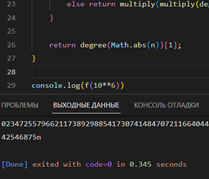
При запуске тестов ошибок не возникло, контрольные числа посчитались быстро и верно. Если запустить эту функцию для n=1000 000, результат найдётся меньше чем за секунду (0, 345 с). |
|
|
Вывод: нахождение n-го числа Фибоначчи через степень матрицы оказалось самым быстрым и при этом дающим верный результат.
ВЫВОДЫ
В ходе работы над проектом я изучил и реализовал в практической деятельности три метода нахождения n-го числа Фибоначчи: рекурсивный, итеративный и матричный. Написал функции, зафиксировал временные затраты при использовании этих методов для нахождения чисел Фибоначчи различной величины.
Данные, полученные в результате компьютерного эксперимента:
|
метод |
Значение n |
||||
|
1000 |
10000 |
100000 |
1000000 |
2000000 |
|
|
рекурсивный |
>10 мин |
крайне долго |
|||
|
итеративный |
0.1 с |
0.1 с |
0.2с |
8.157c |
69.304 c |
|
матричный |
0.1 с |
0.1 с |
0.1 с |
0.345 с |
0.689с |
Исходя из анализа данных, приведенных в таблице можно оценить затраты времени, которое потребовалось для рения задачи.На моём компьютере, чтобы вычислить 1000000-е число Фибоначчи, потребовалось:
8.157секунд при решении итеративным методом;
0.345 секунд матричным методом, что в 23,8 раза быстрее!
Тем самым гипотеза проекта подтверждена. Самым эффективным оказался матричный метод, с помощью которого можно менее чем за секунду находить миллионные члены последовательности Фибоначчи.