В современном мире мы все чаще используем разнообразные машины и гаджеты. Какова роль человека в создании роботов и умении машин решать не только математические, но и логические задачи. Логика (в переводе с греческого) – это упорядоченная система мышления, которая создает взаимосвязи между заданными условиями и позволяет делать умозаключения, основываясь на предпосылках и предположениях.
Актуальность: математический аппарат булевой алгебры нашел широкое применение не только в компьютерном мире, но и при проектировании технических устройств различной природы – электрических, механических и других.
Противоречие: В школе все мы изучаем алгебру, только про булеву алгебру нам не говорили. А в современном мире мы все чаще слышим выражение «булева алгебра». Чем же отличается булева алгебра от школьной, какова история ее появления, задачи и области применения.
Цель: изучить и доказать большое значение булевой алгебры в различных областях науки и практического применения при проектировании технических устройств различной природы.
До середины XIX века о математической логике знали немногие. Большой интерес в научных сообществах вызвал спор, в котором англичанин Джордж Буль заявил о своем намерении создать раздел математики, не имеющий абсолютно никакого практического применения [1]. Как мы помним из истории, в это время активно развивалось промышленное производство, разрабатывались всевозможные вспомогательные машины и станки, т. е. все научные открытия имели практическую направленность. Забегая вперед, скажем, что булева алгебра – самая используемая в современном мире часть математики. Так что спор свой Буль проиграл.
Новым в алгебре Буля является то, что элементы множества, которые в ней изучаются, являются не числами, а высказываниями. Если при решении обычных алгебраических уравнений определяется, какому числу равняется неизвестное X, школьная алгебра ищет ответ на вопрос: «Сколько?»
Алгебра логики ищет ответ на вопрос: «Верно ли то или другое высказывание, обозначенное буквой X?»
Таким образом, алгебра логики может быть использована буквально везде:
Выполнение логических операций можно проиллюстрировать на наглядной физической модели «водопровода» [2]. Представим утверждения, над которыми производятся операции, в виде вентилей на трубах (открытый вентиль — утверждение истинно, закрытый — ложно). Результат операции представим в виде крана, из которого вода может либо течь (истина), либо не течь (ложь). На Рис.1 изображены системы труб, реализующие основные логические операции.
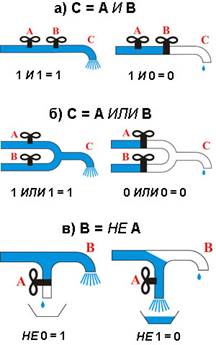
Рис. 1
Например, рассмотрим операцию И: С = А И В (Рис. 1а). Вентили А и В установлены на трубе последовательно, поэтому вода из крана С течет, только если они оба открыты.
Если же установить вентили на две параллельные трубы, соединяющиеся в одну, то такая система будет выполнять операцию ИЛИ: если хотя бы один из вентилей А или В открыт, вода из крана С потечет, т. е. С = А ИЛИ В (рис. 1б).
Результатом моей работы стала математическая электро-викторина. Данная разработка будет полезна учащимся для отработки знаний по разным темам математики: «Формулы площадей геометрических фигур», «Формулы сокращенного умножения» и др. Ученик должен сопоставить картинку с нужной формулой. Если ответ верный – загорается лампочка. Информация проекта стала для меня очень интересной. Я увидела использование теории Буля не только на уроках алгебры, физики, но и на уроках информатики. Думаю, что данная работа имеет место для дальнейшего изучения и использовании в моем обучении и жизни.
