Введение
Линейные и нелинейные регрессии являются инструментом в проведении исследований в эконометрике, в естественно-научных и гуманитарных дисциплинах. Построению линейных и нелинейных регрессионных моделей посвящено много монографий и учебных изданий, в частности монография [1]. Работа [2] была одной из первых работ, посвященных математическому анализу ДНК распределений, полученных в эксперименте.
Существует коммерческое программное обеспечение, которое реализует математическую обработку таких экспериментальных данных [3, 4]. Несмотря на то, что в таких программах предоставлен широкий выбор моделей, при внесении дополнительного биологического материала некоторые параметры распределений пересчитываются, что не совсем отвечает течению биохимических процессов. Решение этой проблемы является актуальной научно-практической задачей.
Цель настоящего исследования – разработать прототип программы построения парной нелинейной регрессии для анализа распределений ДНК, полученных из экспериментальных данных, с учетом возможности фиксировать значения некоторых параметров распределений при добавлении дополнительного биологического материала.
Задачами исследования являются:
· Изучить алгоритм Левенберга-Марквардта построения парной нелинейной регрессии;
· Разработать прототип программы построения парной нелинейной регрессии для набора функций, которые используются или могут быть использованы для анализа распределений ДНК.
Гипотеза исследования. Анализ учебной и научной литературы показывает, что поставленная цель может быть достигнута путем разработки программы и ее тестирования.
Объектом исследования является аппроксимация функции распределения ДНК методом построения парной регрессии.
Предметом исследования является реализация аппроксимации функции распределения ДНК путем построения нелинейной парной регрессии на языке программирования Pascal ABC.
Основная часть
Постановка задачи.
Математически задача построения парной нелинейной регрессии сводится к следующему [1]. Пусть задана табличная зависимость переменной y от переменной x, {yi, xi}, где i = 1, 2, …, M}. Необходимо аппроксимировать данную зависимость функцией f(x, c1, ..., cn), вид которой известен, но ее параметры неизвестны:
 , где i = 1, …, M.
, где i = 1, …, M.
По методу наименьших квадратов минимизируется сумма остатков:

Для решения вычислительной задачи в этой работе использован алгоритм Левенберга-Марквардта [5], который сводится на каждом шаге итерации к решению системы уравнений
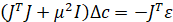
решение которой определяет следующий шаг итерации
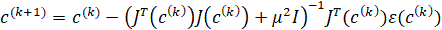
J есть матрица Якоби (матрица первых частных производных функции S по параметрам ci) [5], а JT - транспонированная матрица Якоби, I – единичная матрица, μ(k) - параметр регуляризации, который регулирует не только длину шага, но и направление поиска.
Условие завершение алгоритма
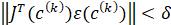
где ||*|| - евклидова норма.
Блок схема алгоритма, реализованный в программе, программы приведена на Рис. 1.

Рис. 1. Блок схема алгоритма Левенберга-Марквардта.
Выбор функций аппроксимации.
Вид функций аппроксимации обсуждался в работах [2, 6]. Нами были рассмотрены и другие функции. В программе могут быть использованы функции вида:
 (1) [2]
(1) [2]
 (2)[6]
(2)[6]
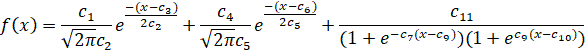 (3)
(3)
 (4)
(4)
Результаты и обсуждение
Тестирование программы было выполнено по данным из работы [2] с функцией вида (2). Были получены следующие оценки коэффициентов: c1 = 67401.88±1.08, c2 = 1.41±2.57х10-05, c3 = 30.64±2.91х10-05, c4 = 9907.36±1.65, c5 = 2.60±0.01, c6 = 62.07±0.01 (c1 = 67400.00±0.14, c2 = 1.41±0.02, c3 = 30.64±0.03, c4 = 9910.00±1.50, c5 = 2.60±0.26, c6 = 62.07±0.27 по данным [2]) . На Рис. 2 приведен график полученной аппроксимации. Коэффициент детерминации [7], равный 0.9999, показывает хорошее соответствие аппроксимирующей кривой с экспериментальными данными.
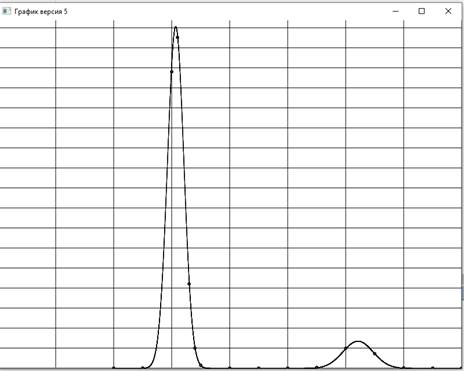
Рисунок 2. График полученной аппроксимации. Шаг сетки по горизонтальной оси 10, а по вертикальной – 5000.
Программа была опробована с функцией вида (2) на экспериментальном наборе из 1024 точек. Были получены следующие оценки коэффициентов: c1 = 1600.36±16.15, c2 = 17.07±0.29, c3 = 285.01±0.23, c4 = 1800.03±47.22, c5 = 60.13±3.34, c6 = 520.80±2.90. На Рис. 3 приведен график полученной аппроксимации. Коэффициент детерминации, равный 0.9376, показывает хорошее соответствие аппроксимирующей кривой с экспериментальными данными.
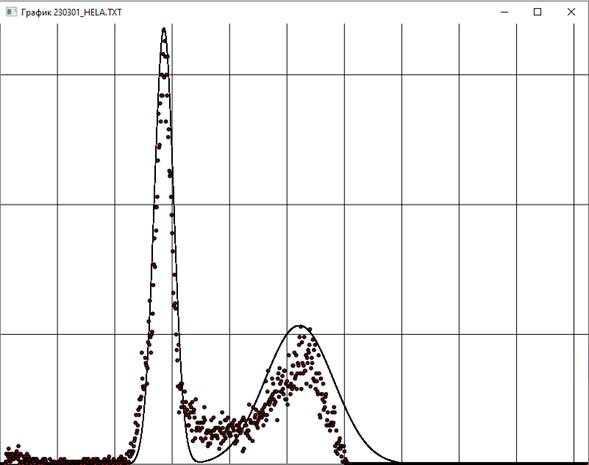
Рис. 3. График полученной аппроксимации. Шаг сетки по горизонтальной оси 100, а по вертикальной – 50.
Программа была выполнена с функцией вида (3) на том же экспериментальном наборе из 1024 точек. Параметры c1-c6 такие же, как и для функции вида (2) выше, c7 = 1.01±0.03, c8 = 300.0±8.21, c9 = 2.03±0.13, c10 = 400.11±5.03, c11 = 10.0±1.63. На Рис. 4 приведен график полученной аппроксимации. Коэффициент детерминации, равный 0.9370, показывает хорошее соответствие аппроксимирующей кривой с экспериментальными данными.
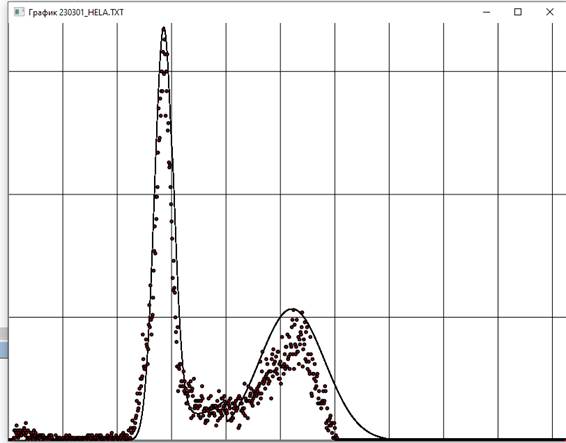
Рис. 4. График полученной аппроксимации. Шаг сетки по горизонтальной оси 100, а по вертикальной – 50.
Выводы
В статье представлен алгоритм прототипа программы построения парной регрессии. Программа предназначена для математического анализа распределений ДНК, полученных с помощью проточной микрофлуорометрии.
Предложено четыре вида функции для построения регрессионной модели.
Приведен результат тестовых испытаний программы, которые показал хорошее соответствие аппроксимирующей кривой с экспериментальными данными с коэффициентом детерминации, равным 0.9999.
Приведен результат работы программы на экспериментальных данных с использование двух видов функций. Показано, что работа программы дакт удовлетворительные результаты.
Эта работа способствует развитию междисциплинарных связем предметов, изучаемых на 1-2 курсах медицинских колледжей..
