Международный школьный научный вестник

Научный журнал для старшеклассников и учителей ISSN 2542-0372

Данная статья является реферативным изложением основной работы. Полный текст научной работы, приложения, иллюстрации и иные дополнительные материалы доступны на сайте II Международного конкурса научно – исследовательских и творческих работ учащихся «Старт в науке» по ссылке: https://www. school – science. ru/2017/7/26863

К свойствам функции относится область значений функции. Проблема нахождения области значений, например, дробно – рациональной функции, привела к необходимости ознакомиться со способами ее нахождения.

Цель исследования: найти различные методы нахождения области значений дробно – рациональных функций. Задачи исследования:

1). Ознакомиться со способами решения задач на нахождение области значений функции;

2). Изучить инверсию функций;

3). Использовать алгебраические неравенства для нахождения области значений функции;

4). Составить банк функций с нахождением области значений функций различными методами. Сравнить эти методы с точки зрения затрат времени и трудоёмкости;

5). Использовать программу Graphи различные свойства функций для построения графиков функций. При ознакомлении с некоторыми методами нахождения области значений функции в различных источниках, указанных ниже, не нашлось таких примеров решения, в которых бы использовались различные методы. В данной исследовательской работе сопоставляются разные, возможные, методы нахождения области значений функции для выделения самого рационального.

Глава I. Теоретическая часть

§1. Некоторые сведения об области значений функции.

Определение области значений функции. Областью (множеством) значений E(у) функции y = f(x) называется множество таких чисел y0, для каждого из которых найдётся такое число x0, что: f(x0) = y0.

Свойства функций, используемые при нахождении области значений функции

Для успешного нахождения области значений функции надо хорошо знать свойства основных элементарных функций, особенно их области определения и характер монотонности. Приведём свойства функции, которые учитываются при нахождении Е(у):непрерывность;монотонность;дифференцируемость;чётность, нечётность;обратимость;периодичность и т. д.

Известны следующие способы нахождения областей значений функций:а) последовательное нахождение значений сложных аргументов функции;б) метод оценок;в) использование свойств непрерывности и монотонности функции;г) использование производной;д) использование наибольшего и наименьшего значений функции;е) графический метод;ж) метод введения параметра;з) метод обратной функции. [4].Определение. Параметром называется независимая переменная, значение которой в задаче считается заданным фиксированным или произвольным действительным числом, или числом, принадлежащим заранее оговоренному множеству. Определение. Обра?тная фу?нкция — функция, обращающая зависимость, выражаемую данной функцией. Например, если функция от x даёт y, то обратная ей функция от y даёт x.

§2. Инверсия

Известна теорема о том, что если функция 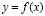возрастает и принимает только положительные значения, то функция 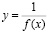убывает.

Целесообразно рассматривать преобразования плоскости, при которых точки с координатами 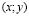переходят в точки с координатами 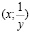, ибо легко заметить, что

именно с помощью такого преобразования можно построить рассмотренный график.

Определение:

Точка В называется инвертной точке А относительно данной прямой (оси) l, если:

эти точки лежат по одну сторону относительно оси l;

отрезок, их соединяющий, перпендикулярен оси l;

произведение расстояний от этих точек до оси l равно 1.

У точек оси инвертных точек нет.

Определение:

Преобразование плоскости, при котором каждая точка переходит в инвертную ейотносительно данной прямой, называется инверсией. Для точек этой прямой преобразование не определяется.

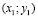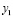
Замечание. При инверсии относительно осиОх точка А с координатами , , 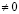переходит в точку В с координатами 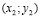, где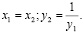

В самом деле, 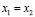, так как отрезок АВ перпендикулярен осиОх, 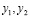должны быть одного знака, так как А и В лежат в одной полуплоскости относительно оси Ох, наконец, 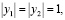так как произведение расстояний от А и В до оси равно единице, т. е.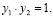

Свойства инверсии. Построение графиков.

А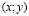 – неподвижная точка инверсии относительно осиОх тогда и только тогда, когда 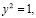т. е. 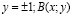– неподвижная точка инверсии относительно оси Оутогда и только тогда, когда 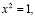т. е.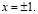

Чем дальше от оси инверсии точка, тем ближе к ней инвертная ей точка.

Теорема: График функции

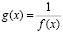
получается из графика функции 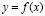инверсией относительно оси Ох.

Теорема: График функции

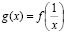
получается из графика функции 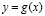преобразованием инверсии относительно оси Оу.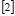

§3. Некоторые неравенства, используемые в работе.

Доказательства некоторых неравенств (проведенные самостоятельно).

Неравенство 1.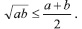

Доказательство.

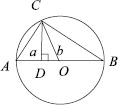
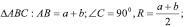
Теорема о высоте:

CD =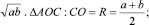

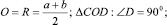
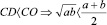
в частном случае, если 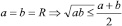ч. т. д.

Неравенство 2

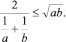
Доказательство.

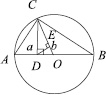
Преобразуем выражение:

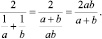
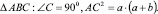
По теореме катета:

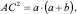
По теореме Пифагора:

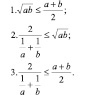
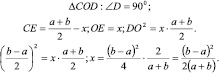
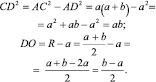
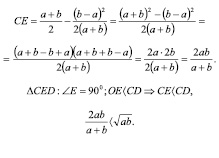
В частности, если 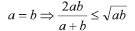Ч. т. д.

Неравенство 3.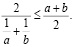

Доказательство: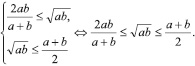 

Значит, 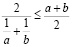, ч. т. д.

Заключение

Данная тема имеет практическое применение, так как при изучении тех или иных процессов из реальной жизни, описываемых математическими формулами, чаще всего вычисляют значения функций. В школьном курсе математики изучается тема «Область значения функции». Такие задачи обязательно содержатся в заданиях различных математических тестов, в частности в заданиях единого государственного экзамена. Если выбирать универсальный способ нахождения области значений функции, то это графический с применением производной, таких свойств как четность, асимптоты, нули функции. Удобно использовать инверсию для построения график функций, но не все функции инвертируются. Если есть выбор способов, то к рациональным способам можно отнести и введение параметра и метод обратной функции.

Знание различных способов решения одной и той же задачи позволяет осуществить проверку полученных результатов.