Международный школьный научный вестник

Научный журнал для старшеклассников и учителей ISSN 2542-0372

• Авторы
• Научный руководитель
• Файлы
• Литература

Мальцев М.И. 1

---

1 ГАОУ ТО «ФМШ», 11 класс

Тарасов О.А. (, ГАОУ ТО «ФМШ»)

Статья в формате PDF

0 KB

1. Уипл Ф.Л. Семья Солнца: Планеты и спутники Солнечной системы / Пер. с англ. Ю.И. Ефремова. – М.: Мир, 1984. – C. 169–264.

2. Уральская В.С. Спутниковые системы планет // Земля и Вселенная. – 2002. – № 2. – C. 3–15.

3. Зигель Ф.Ю. Астрономия в ее развитии. – М.: Просвещение, 1988.

4. Спутники Юпитера // Википедия. – http://ru.wikipedia.org.

5. Розивика И . Танцы спутников Юпитера. // Звездочет: научно-популярный астрономический журнал. – 1998. – №8. – C. 26–29.

6. Томилин А.Н. Небо Земли. Очерки по истории астрономии. – Л.: Детская литература, 1974. – C. 136–138.

Изучение Вселенной, один из самых благородных и смелых подвигов человеческого разума.

Р.З. Сагдеев

К концу 2018 года в Солнечной системе известно почти 200 ее крупных членов – 8 больших планет и 185 спутников. Процесс изучения Солнечной системы активно происходит и в наше время. В ближайшем будущем можно ожидать открытие новых спутников планет, а также других небесных тел за орбитой Плутона. Для того, чтобы открыть новые спутники планет нужны мощные телескопы. Эта задача, пока, нам не по силам.

В рамках данной работы мы поставили перед собой более скромную цель – доказать, что с помощью обычного цифрового фотоаппарата можно получить изображения галилеевых спутников Юпитера, а затем, по этим изображениям рассчитать период обращения этих спутников.

Такие методики наблюдения и расчетов были бы полезны в преподавании предмета «Астрономия» в школе, дисциплины «Астрофизика» в вузе, а также, интересны для отдельных любителей астрономии и астрономических клубов.

Задачи исследования:

1. Вывести формулу для расчета периода спутника планеты по ее угловым расстояниям и позиционным углом в разные моменты времени.

2. С помощью недорогого цифрового фотоаппарата с ультра-зум объективом получить изображения Юпитера с его спутниками текущим летом.

3. Обработать результаты вычислить периоды спутников по выведенной формуле, сравнить результаты с точными значениями, сделать выводы.

4. Подготовить лабораторную работу по определению периодов спутников Юпитера для учеников физико-математической школы Тюменской области.

5. Опубликовать данное исследование в российском журнале любителей астрономии «Звездочет».

Объект исследования – орбиты спутников Юпитера.

Предмет исследования – методика определения периодов спутников планет.

1. Экспериментальная часть

1.1. Получение фотографий

Для получения изображений спутников Юпитера нужен фотоаппарат с фокусным расстоянием объектива F более 300 мм, так как при меньшем F из-за мелкого масштаба кадра изображения Юпитера и спутников сольются друг с другом. Мы использовали фотоаппарат Olympus SP-500, который имел F=380 мм. Чтобы избежать дрожания изображения, мы закрепили фотоаппарат на треножнике ECSA-3750, рис. 1. Снимали с максимальным разрешением фотоаппарата в 6 мегапикселей и минимальным сжатием изображения. Лучшие из полученных снимков за шесть дней наблюдений приведены на рис. 2.

Рис. 1. Фотоаппарат Olympus SP-500 на треножнике ECSA-3750.

1.2. Расчет поля зрения фотоаппарата и масштаба кадра

Определим угол поля зрения фотоаппарата в горизонтальной плоскости, α, при фокусном расстоянии объектива F=380 мм. Указанное фокусное расстояние соответствует горизонтальному размеру кадра L = 36 мм.

Из треугольника ABC имеем

,

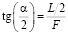тогда

;

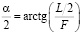окончательно

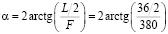= =2∙2.71° = 5,42°.

Выразим теперь поле зрения фотоаппарата сначала в минутах дуги, а потом в секундах дуги. Это сделать просто, т.к. в одном градусе 60 минут дуги (т.е. 1° = 60′), а в одной минуте дуги 60 секунд дуги (т.е. 1′ = 60″). Тогда

α = 5. 42° = 5.42′60′ = 325,2′ = 325,2′60″ = =19512″.

Горизонтальные и вертикальные размеры кадра при разрешении 6 МПс были 2816 и 2112 пикселей, соответственно.

Тогда масштаб кадров был

19512″ / 2816 пикселей = 6.93″ в одном пикселе.

1.3. Определение углового расстояния спутников по фотографиям в программе Microsoft Paint

Полученные снимки Юпитера и его спутников обрабатывали в программе Microsoft Paint. Выделяли на снимке такой прямоугольный участок изображения, чтобы одна из вершин прямоугольника попала в центр изображения спутника, а противоположная ей вершина – в центр изображения Юпитера, рис. 3.

Инструмент «Выделение» позволяет определить ширину W и высоту H прямоугольника в пикселях, информация о которых появляется в нижнем поле окна программы. Линейное расстояние r между спутником и планетой – это расстояние, равное диагонали прямоугольника. По теореме Пифагора это расстояние легко рассчитать, как

.

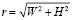К примеру, на рис. 3 имеем W= 71 пиксель, H= 14 пикселей. Тогда

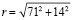= 72.4 пикселя.

Рассчитав линейное расстояние r между спутником и Юпитерам в пикселях, можно перейти к определению углового расстояния a между ними. Так, для рис. 2 мы получили r= 72.4 пикселя. Значит, угловое расстояние равно α = 72.4 пикселя′ 6.93 (секунд дуги / пиксель)″ 502 секунды дуги.

Результаты расчета угловых расстояний спутников Юпитера по снимкам (рис. 2) за шесть дней наблюдений приведены в табл. 2. Видно достаточно хорошее совпадение расчетных (в программе StarCalc) и наблюдаемых величин угловых расстояний.

1.4. Определение положения спутников в программе StarCalc

Четыре галилеевых спутника Юпитера имеют очень близкую яркость, поэтому различить их при наблюдениях друг от друга невозможно (см. табл. 1).

Таблица 1

Средняя яркость спутников на период наблюдений

Для определения положения спутников мы пользовались программой StarCalc версии 5.73, которую написал российский любитель астрономии и программист из г. Воронежа А.Е. Завалишин.

В отдельном окне программы можно получить информацию о линейном угле, о позиционном угле j и угловом расстоянии a спутников от планеты. Эти данные для шести моментов времени наших наблюдений приведены в табл. 2, ниже. Расчетные и полученные из наблюдений значения a имеют хорошее совпадение. Методика расчета приведена в следующей главе.

2 июля 2018 3 июля 2018

8 июля 2018 9 июля 2018

11 июля 2018 13 июля 2018

Рис. 2. Фотографии Юпитера и его спутников (внизу) и их взаимные положения (вверху), рассчитанные в программе StarCalc, на те же моменты местного времени – 23°°. Изображения Юпитера и спутников вытянуты вследствие вращения небесной сферы (вызванной вращением Земли вокруг оси). Длительность снимков от 2 до 5 секунд

Рис. 3. Вид окна программы Microsoft Paint при определении углового расстояния r спутника от Юпитера

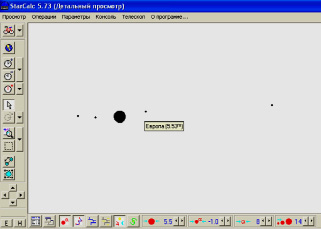
Рис. 4. Вид окна программы StarCalc в масштабе 43600 % с Юпитером и его спутниками.

Таблица 2

Данные о Юпитере и его четырех галилеевых спутниках, рассчитанные в программе StarCalc и полученные из наблюдений

Примечания:

1 а.е. = 149.6 млн. км

4,44 а.е. = 664.22 млн. км

Наблюдения проводились в 2300 по местному времени.

Прочерк означает отсутствие данных, из-за того, что спутник имел слишком малое угловое расстояние от Юпитера и потерялся в его блеске (смотри, например, фото за 13 июля на рис. 2).

2. Расчетная часть

2.1. Расчет периода обращения спутников Юпитера

Пусть R – это радиус орбиты спутника Юпитера, а φ – это позиционный угол спутника (рис. 5). Тогда при наблюдениях с Земли спутник имеет линейное расстояние от Юпитера r.

Из треугольника АВС следует, что радиус орбиты и линейное расстояние спутника связаны, как

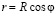. (1)

Спутник движется по своей орбите с постоянной угловой скоростью w. Поэтому угол φ меняется по линейному закону от времени t

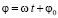, (2)

где φ0 – начальный позиционный угол в момент времени t= 0.

При наблюдениях с Земли линейному расстоянию (удалению) r спутника от Юпитера соответствует угловое расстояние (угол) α. Из треугольника ACE следует, что угол α связан с линейным расстоянием r спутника от Юпитера и с расстоянием от Земли до Юпитера l как

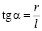. (3)

Поскольку расстояние от Земли до Юпитера велико (на момент наших наблюдений около 664.22 млн. км), а радиус орбиты самого удаленного из четырех галилеевых спутников – Каллисто равен 1.88 млн. км, то угол a очень мал. Для спутника Каллисто он не превышает a = arctg(1.88/664.22) = =arctg (0.0028) = 0.16°, а для трех более близких галилеевых спутников еще меньше. Это мы учтем далее при выводе формулы.

Подставив в формулу (3) формулы (1) и (2) имеем

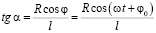. (4)

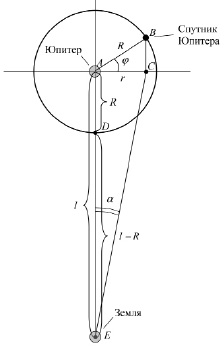
Рис. 5. К расчету периода обращения спутника

Пусть мы наблюдаем спутник Юпитера в два момента времени t1 = 0 и t2 = Dt. Им соответствуют два значения углового расстояния спутника от планеты a1 и a2, для которых, согласно (4), справедливо

,

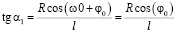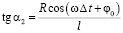
и, следовательно

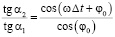. (5)

Так как величины α1 и α2 << 1°, то

.

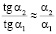Следовательно, формулу (5) можно упростить до

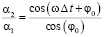. (6)

Угловая скорость w связана с периодом обращения T спутника как

.

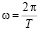Заменив w в формуле (6) имеем

.

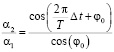Тогда, выражая искомый период T, имеем

;

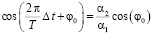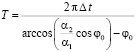. (7)

Расчеты периодов обращения галилеевых спутников Юпитера будем делать, в дальнейшем, по формуле (7).

2.2. Результаты расчетов и их обсуждение

По данным табл. 2 мы рассчитали периоды обращения Ганимеда и Каллисто вокруг Юпитера.

Для Ганимеда использовали пары данных о его позиционном угле и угловом расстоянии 2–3 июля, 8–9 июля и 11–13 июля.

Для Каллисто использовали пары данных за 2–3 июля и 11–13 июля. Данными за 8–9 июля воспользоваться было нельзя, т.к. 8 июля Каллисто был расположен близко к Юпитеру и их изображения слились (рис. 2). Поэтому данные об угловом расстоянии Каллисто за 8 июля отсутствовали.

Периоды обращения Ио и Европы рассчитаны не были, т.к. за интервал времени между наблюдениями (одни сутки) эти спутники смещались более чем на 45° по позиционному углу (а именно, на 360°/1.77 = =203.4° и 360°/3.55 = 101.4°) и тогда формула (7) неприменима.

Для расчетов по формуле (7) необходимо привести значения позиционного угла к диапазону 0–45°. Это легко сделать вычитанием из действительного значения угла величины в 90°, 180° или 270°. Результаты расчетов периодов обращения Ганимеда и Каллисто приведены в таблице 3.

Для наглядности покажем пример расчетов для Ганимеда по данным за 2–3 июля. Из таблицы 2 находим, что позиционный угол Ганимеда 2 июля равен 277°. Тогда приведенный угол равен 277° – 270° = 7°. Интервал времени Dt между наблюдениями (2 и 3 июня) равен 1 сутки. Подставляя теперь данные за 2 и 3 июня в формулу (7), и пользуясь тем, что в 1 радиан = 57.3°, получим период обращения Ганимеда в сутках

.

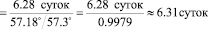Таблица 3

Приведенные значения позиционных углов, наблюдаемые значения угловых расстояний и рассчитанные значения периодов обращения Ганимеда и Каллисто

Рассчитанные значения периодов обращения Ганимеда (три значения) и Каллисто (два значения) соответственно усреднили и получили 6.36 и 18.27 суток. Полученные средние результаты периодов обращения находятся в достаточно хорошем соответствии с истинными значениями периодов в 7.16 и 16.69 суток. Относительные погрешности определения периодов обращения Ганимера и Каллисто составили соответственно

(7.16 – 6.36)′ 100 % / 7.16 » 11,2 %;

(18.27 – 16.69)′ 100 % / 16.69 » 9,5 %.

Это очень неплохо, учитывая, что мы использовали далеко не профессиональную астрономическую аппаратуру.

Выводы

1. Мы доказали на практике, что с помощью обычного недорогого цифрового ультра-зум фотоаппарата можно получить изображения всех четырех галилеевых спутников Юпитера.

2. Кроме того, мы установили, что при попиксельной обработке полученных снимков можно определить угловые расстояния спутников от Юпитера с точностью порядка 10 %.

3. Это дает возможность с помощью выведенной нами формулы определить периоды спутников с точностью около 10 %.

4. Полученный практический результат позволил подготовить лабораторную работу по определению периодов спутников Юпитера, которая проводится в рамках предмета «Астрономия» для учеников физико-математической школы Тюменской области.

5. Проанализировав советскую и современную учебную и методическую литературу по астрономии, мы с удивлением обнаружили, что в ней отсутствуют лабораторные работы по определению периода спутников планет. Это кажется досадным упущением, особенно в свете теперешнего развития любительской фотоаппаратуры. Мы надеемся, что наше исследование поможет исправить этот недостаток и сделает астрономию для многих нагляднее и ближе.

Библиографическая ссылка