Данная статья является реферативным изложением основной работы. Полный текст научной работы, приложения, иллюстрации и иные дополнительные материалы доступны на сайте VII Международного конкурса научно-исследовательских и творческих работ учащихся «Старт в науке» по ссылке: https://school-science.ru/7/7/39073.
Работа посвящена решению 19 задачи из ЕГЭ по математике, а также методам решения нестандартных олимпиадных задач. Поскольку данные задачи не рассматриваются в школьной программе, то их решение вызывает большие затруднения у учащихся. Множество решений таких задач колоссально, и каждый подвид имеет свои особенности и свойства. Но на основании проведенных исследований было выяснено, что эти задачи не имеют единого алгоритма решения. Однако стоит отметить, что в зависимости от вида, они обладают определенным методом решения, а иногда могут быть решены разными способами. На основании проведенной работы, совместно с научным руководителем разрабатывается методическое пособие, которое будет использоваться при проведении элективных курсов по математике в ГБОУ СОШ № 5 «ОЦ» г. Новокуйбышевска Самарской области.
Ключевые слова: 19 задача из ЕГЭ, метод, простые числа, теория чисел.
Решая экзаменационные задачи, мы часто сталкиваемся с проблемой решения 19 задачи, многие выпускники не справляются с решением этой задачи. Решение данных задач, как правило, вызывают большие затруднения. К сожалению, школьная программа и элективные курсы не уделяют должного внимания изучению этого аспекта математики. Целью моего исследования является – выявить алгоритм решения нестандартной задачи № 19. Проведя анализ литературы по данным задачам, я пришла к выводу, что решение этих задач представляет собой одну из труднейших проблем теории чисел. Тема теория чисел привлекла внимание многих выдающихся математиков. Ими занимались такие ученые, как: Пьер Ферма (1601-1665) и Л. Эйлер (1707-1783). Все вышеперечисленные факторы определяют актуальность исследования.
Анализ литературных данных и результаты ранее проведенных исследований позволили выявить проблему исследования: «Возможно, ли найти легкое решение задачи № 19 из ЕГЭ по математике профильного уровня?»
Актуальность и недостаточная проработанность данной проблемы обусловили тему исследования: «Решение 19 задачи из ЕГЭ».
Цель исследования: выявить способы решения 19 задачи из ЕГЭ по математике профильного уровня.
Объект исследования – решение 19 задачи из ЕГЭ.
Предмет исследования – применение теоремы Фробениуса при решении нестандартных задач по математике.
Гипотеза: «Знание и умение применять теорему Фробениуса значительно облегчают решение 19 задачи из ЕГЭ».
Исходя из цели и предмета исследования, для доказательства гипотезы были поставлены и решены следующие задачи:
1. Провести глубокий анализ литературы о методах решения 19 задачи из ЕГЭ.
2. Рассмотреть теорему Фробениуса.
3. Провести анализ решения 19 задачи из ЕГЭ с применением теоремы Фробениуса.
Для достижения цели и решения поставленных задач применен комплекс методов исследования:
– теоретические: изучение и анализ литературы и научно-исследовательских работ по теме исследования;
– эмпирические: наблюдение, опрос, анкетирование, проведение опытно-экспериментальной работы.
Анализ 19 задачи из ЕГЭ по математике профильного уровня
ЕГЭ по математике является обязательным экзаменом любого школьника в 11 классе, соответственно к нему уделяется больше внимания, поэтому информация, представленная в данном разделе актуальна для всех. Экзамен по математике делится на два вида – базовый и профильный. Как правило, большинство выпускников сдают профильный уровень математики для поступления в вузы, и стремятся успешно сдать его. Для того чтобы получить максимальные баллы, нужно сделать 16, 17, 18 – за них дают по 3 первичных балла и в особенности 19 – за правильное решение которой, начисляют 4 первичных балла.
Нас заинтересовала 19 задача из ЕГЭ по математики, и мы решили выяснить какие виды таких задач встречается. Анализ литературы и всевозможные сборники задач для подготовки к ЭГЭ по математике профильный уровень, показал, что в 19 задачу входят нестандартные, многие олимпиадные виды задач. Такие задачи не входят в школьный курс математике, а лишь частично разбираются на элективных курсах в старших классах.
Мы провели анализ результатов решения 19 задачи на ЕГЭ по математике за 2017-2018 годы среди российских выпускников. Были получены следующие результаты.
Ненулевые баллы получило около 17 % участников экзамена, 1 балл – около 15 %. Первый пункт выполнили те, кто прочитал условие, понял закономерности, попробовал исследовать несколько примеров, а потом обобщить полученный результат. Типичным заблуждением для многих оказалось, что на вопрос «Может ли?» нужно давать аргументированное решение, а не ответ «да» или «нет».
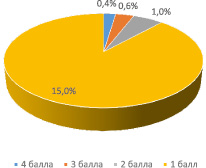
Статистика выполнения задачи № 19 на ЭГЭ «Математика профильный уровень» за 2017-2018 г.
Проведенный анализ показал, что маленький процент выпускников справились с рассматриваемой задачей. Что подтвердило актуальность исследования методов и способов решения задачи № 19. В задаче № 19 может встречаться различные по темам задачи. Мы заметили, что большинство задач относятся к разделу математики «Теория чисел».
Теория чисел, или высшая арифметика, – раздел математики, первоначально изучавший свойства целых чисел. В современной теории чисел рассматриваются и другие типы чисел – например, алгебраические и трансцендентные, а также функции различного происхождения, которые связаны с арифметикой целых чисел и их обобщений. В исследованиях по теории чисел, наряду с арифметикой и алгеброй, применяются геометрические и аналитические методы, а также методы теории вероятностей [1]. Методы теории чисел широко применяются в криптографии, вычислительной математике, информатике.
В элементарной теории чисел целые числа изучаются без использования методов других разделов математики. Среди основных тематических направлений элементарной теории чисел можно выделить следующие:
1. Теория делимости целых чисел.
2. Алгоритм Евклида для вычисления наибольшего общего делителя и наименьшего общего кратного.
3. Разложение числа на простые множители и основная теорема арифметики.
4. Теория сравнений по модулю.
5. Цепные дроби.
6. Диофантовы уравнения, то есть решение неопределённых уравнений в целых числах.
7. Изучение некоторых классов целых чисел – числа Фибоначчи и др.
8. Малая теорема Ферма и её обобщение: теорема Эйлера.
9. Нахождение пифагоровых троек, задача о четырёх кубах.
10. Занимательная математика – например, построение магических квадратов
В аналитической теории чисел для вывода и доказательства утверждений о числах и числовых функциях используется мощный аппарат математического анализа (как вещественного, так и комплексного), иногда также теория дифференциальных уравнений. Это позволило значительно расширить тематику исследований теории чисел. В частности, в неё вошли следующие новые разделы [2].
1. Распределение простых чисел в натуральном ряду и в других последовательностях (например, среди значений заданного многочлена).
2. Представление натуральных чисел в виде сумм слагаемых определённого вида (простых чисел, квадратов и т.д.).
3. Диофантовы приближения.
Проанализируя литературу по аналитической теории чисел, мы столкнулись с теоремой Фробениуса – одной из теорем общей алгебры.
В следующем параграфе рассмотрим биографию великого ученого, его вклад в математику, а также его теорему и следствия.
Теорема Фробениуса
Обратимся к биографии великого ученого Фердинанда Георга Фробениуса (1849-1917). Фробениус – немецкий математик, известный своим вкладом в теорию эллиптических функций, дифференциальных уравнений и теории групп. Он также был первым, кто ввёл понятие рациональной аппроксимации функций, и дал первое полное доказательство теоремы Гамильтона – Кэли. Также он внёс свой вклад в определение дифференциально-геометрических объектов в современной математической физике, известных ныне как многообразия Фробениуса.
Основные его работы относятся к теории групп, в частности, к теории представлений.
Теорема Фробениуса – одна из теорем общей алгебры. Теорема утверждает, что при некоторых естественных предположениях всякое тело, расширяющее поле вещественных чисел: либо изоморфно исходному полю; либо изоморфно полю комплексных чисел; либо изоморфно телу кватернионов.
Множество областей математики и информатики находят применение в решении этой задачи. Среди них: эллиптические кривые, алгебраическая теория чисел и квантовые вычисления.
Теорема взаимности Фробениуса и унитарности матрицы рассеяния накладывают дополнительные условия на ее элементы и сокращают число независимых параметров, определяющих матрицу рассеяния. Для реакции, идущей по N возможным каналам, комплексная матрица рассеяния содержит два вещественных параметров.
Автоморфизм Фробениуса – автоморфизм конечного поля над полем, где q – степень простого числа. Группа автоморфизмов над носит также название группы Галуа поля над. Группа Галуа над является циклической, а значит, поле является циклическим расширением поля [2].
Фробениус сделал существенный вклад в теорию конечных групп линейных подстановок. В теории групп известны так называемые корневые группы Фробениуса, над которыми позже работал Шур. Фробениус создал теорию характеров групп. Ему также принадлежит строгое изложение метода суммирования средними арифметическими, широко применяемого в учении о расходящихся рядах. Он также был первым, кто ввёл понятие рациональной аппроксимации функций (ныне известный как аппроксимации Паде), и дал первое полное доказательство теоремы Гамильтона – Кэли.
Теорема (Фробениуса-Перрона)
Пусть L – тело, содержащее в качестве подтела тело R вещественных чисел, причём выполняются два условия:
1. любой элемент LxL коммутирует по умножению с вещественными числами: xa = ax, R;
2. L является конечномерным векторным пространством над полем R.
Другими словами, L является конечномерной алгеброй с делением над полем вещественных чисел.
Теорема Фробениуса утверждает, что всякое такое тело L:
- либо изоморфно полю R вещественных чисел,
- либо изоморфно полю C комплексных чисел,
- либо изоморфно телу H кватернионов.
Отметим, что теорема Фробениуса относится только к конечномерным расширениям R. Например, она не охватывает поле гипервещественных чисел нестандартного анализа, которое тоже является расширением R, но не конечномерным. Другой пример, алгебра рациональных функций.
Дадим определения основных понятий, используемых в теореме.
Поле в общей алгебре – множество, для элементов которого определены операции сложения, взятия противоположного значения, умножения и деления (кроме деления на нуль), причём свойства этих операций близки к свойствам обычных числовых операций.
Объекты, между которыми существует изоморфизм, являются в определённом смысле «одинаково устроенными», они называются изоморфными.
Кватернионы – система гиперкомплексных чисел, образующая векторное пространство размерностью четыре над полем вещественных чисел.
Комплексное число – это выражение вида a + bi, где a, b – действительные числа, а i – так называемая мнимая единица, символ, квадрат которого равен –1, то есть i2 = –1. Число a называется действительной частью, а число b – мнимой частью комплексного числа z = a + bi. Если b = 0, то вместо a + 0i пишут просто a.
2. Следствия и замечания.
Эта теорема тесно связана с теоремой Гурвица о нормированных вещественных алгебрах. Нормированные алгебры с делением – только R ,C , H и (неассоциативная) алгебра чисел Кэли.
При расширении системы комплексных чисел мы неизбежно теряем какие-либо арифметические свойства: коммутативность (кватернионы), ассоциативность (алгебра Кэли) и т.п.
Не существует аналога системы кватернионов с двумя (а не тремя) кватернионными единицами.
Поля R и C являются единственными конечномерными вещественными ассоциативными и коммутативными алгебрами без делителей нуля.
Тело кватернионов H является единственной конечномерной вещественной ассоциативной, но некоммутативной алгеброй без делителей нуля.
Алгебра Кэли является единственной конечномерной вещественной альтернативной неассоциативной алгеброй без делителей нуля.
Три последних утверждения образуют так называемую обобщённую теорему Фробениуса.
3. Алгебры с делением над полем комплексных чисел.
Алгебра размерности n над полем C комплексных чисел является алгеброй размерности 2n над R . Тело кватернионов H не является алгеброй над полем C, так как центром H является одномерное вещественное пространство. Поэтому единственной конечномерной алгеброй с делением над C является алгебра C.
4. Гипотеза Фробениуса.
Гипотеза Фробениуса утверждает, что и без условия ассоциативности при n, отличном от 1, 2, 4, 8, в вещественном линейном пространстве Rn нельзя определить структуру алгебры с делением. Гипотеза Фробениуса доказана в 60-х гг. XX века.
Если при n > 1 в пространстве Rn определено билинейное умножение без делителей нуля, то на сфере Sn-1 существует n-1 линейно независимых векторных полей. Из результатов, полученных Адамсом о количестве векторных полей на сфере, следует, что это возможно только для сфер S1, S3, S7. Это доказывает гипотезу Фробениуса [6].
Данную теорему можно применять при решении нестандартных математических задач, в том числе и некоторые виды 19 задачи из ЭГЭ по математике профильный уровень.
Таким образом, существует большое количество разновидностей 19 задачи из ЕГЭ и, соответственно, различные алгоритмы их решения. В следующем параграфе покажем применение теоремы Фробениуса при решении нестандартных задач.
Применение теоремы Фробениуса при решении задач
Результаты проведенного опроса и ранее проведенных исследований показали, что нестандартные задачи, как правило, вызывает большие затруднения. Рассмотрим подробнее решение таких задач, которые могут встретится в 19 задаче ЕГЭ профильный уровень, а также на олимпиадах.
Задача 1: Пусть множество называется хорошим, если существует возможность разбить это множество на два подмножества, суммы элементов в которых одинаковы.
а) является ли хорошим множество {200; 201; 202; …; 299}?
б) является ли хорошим множество {2; 4; 8; …; 2100}?
в) каково число хороших четырёхэлементных подмножеств у множества {1; 2; 4; 5; 7; 9; 11}?
Решение. а) Предположим, что данное множество является хорошим. Итак, попытаемся разбить наше множество на два подмножества, суммы элементов в которых будут одинаковы.Группируем элементы исходного множества в пары: первый с последним, второй с предпоследним и так далее:
{200;299}, {201;298}, {202;297}, {249;250}.
Последняя пара будет состоять из двух чисел: 249 и 250. Всего таких пар получится 50. Сумма чисел в каждой паре равна 499. А дальше берите, какие угодно 25 пар в первое множество, остальные 25 – во второе множество, и получите требуемое разбиение.
б) Задание то же самое, только множество другое. Нам требуется разбить данное множество на два подмножества, суммы элементов в каждом из которых равны. Нужно посчитать сумму элементов нашего исходного множества. Перед нами классическая геометрическая прогрессия со знаменателем q = 2, первым членом b_1 = 2 и n = 100 элементами. Сумма всех элементов такой прогрессии определяется по известной формуле:
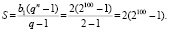
Если бы мы разбили наше множество на два подмножества с одинаковой суммой элементов в каждом из них, то эта сумма оказалась бы равной 2^100-1. А это нечётное число. Но ведь все элементы нашего множества – это степени двойки, то есть числа, безусловно, чётные.
в) Сколько же четырёхэлементных хороших множества содержится во множестве {1; 2; 4; 5; 7; 9; 11}? Итак, как же нам свести это задание к осознанному перебору?
Суммы искомых хороших четырёхэлементных подмножеств должны быть чётными, иначе их нельзя разбить на подмножества с одинаковыми суммами элементами. При этом минимально возможная сумма равна 1 + 2 + 4 + 5 = 12, а максимально возможная сумма равна 5 + 7 + 9 + 11 = 32. Таких сумм 11 штук. Чётные числа 2 и 4 должны либо одновременно входить в хорошее четырёхэлементное множество, либо одновременно не входить в него. В противном случае только одно из чисел четырёхэлементного множества чётное, поэтому сумма элементов такого множества не будет чётной. Поскольку порядок расположения элементов в искомых хороших четырёхэлементных множествах не важен, значит, элементы в этих множествах будут у нас расположены по возрастанию.
Рассматриваем все возможные суммы:
Сумма 12: {1; 2; 4; 5}; сумма 14 {1; 2; 4; 7}; сумма 16: нет вариантов; сумма 18: {2; 4; 5; 7};сумма 20: нет вариантов; сумма 22: {2; 4; 7; 9}, {2; 4; 5; 11}; сумма 24: {1; 5; 7; 11}; сумма 26: {2; 4; 9; 11}; сумма 28: нет вариантов; сумма 30: нет вариантов; сумма 32: {5; 7; 9; 11}. Вот и получилось у нас всего 8 множеств. Других вариантов нет.
Ответ: а) да; б) нет; в) 8
Задача 2: На доске написано более 40, но менее 48 целых чисел. Среднее арифметическое этих чисел равно –3, среднее арифметическое всех положительных из них равно 4, а среднее арифметическое всех отрицательных из них равно –8.
а) Сколько чисел написано на доске?
б) Каких чисел написано больше: положительных или отрицательных?
в) Какое наибольшее количество положительных чисел может быть среди них?
Решение:
1. Пусть среди записанных на доске чисел положительных k. Отрицательных чисел l и нулевых m.
2. Сумма выписанных чисел равна их количеству в данной записи на доске, умноженному на среднее арифметическое. Определяем сумму:
4k – 8l + 0⋅m = – 3(k + l + m)
3. Заметим, что слева в приведенном только что равенстве каждое из слагаемых делится на 4, потому сумма количества каждого типа чисел k + l + m тоже делится на 4. По условию общее число записанных чисел удовлетворяет неравенству:
40 < k + l + m < 48
Тогда k + l + m = 44, потому что 44 единственное между 40 и 48 натуральное число, которое делится на 4. Значит, написано на доске всего 44 числа.
4. Определяем, чисел, какого вида больше: положительных или отрицательных. Для этого приведем равенство 4k – 8l = – 3(k + l + m) к более упрощенному виду: 5l = 7k + 3m.
5. m ≥ 0. Отсюда вытекает: 5l ≥ 7k, l > k. Получается, что отрицательных чисел записано больше положительных. Подставляем вместо k + l + m число 44 в равенство
4k – 8l = – 3(k + l + m).
Имеем
4k – 8l = –132, k = 2l – 33
k + l ≤ 44, тогда получается: 3l – 33 ≤ 44; 3l ≤ 77; l ≤ 25; k = 2l – 33 ≤ 17. Отсюда приходим к выводу, что положительных чисел не более 17. Если же положительных чисел всего 17, то на доске 17 раз записано число 4, 25 раз – число –8 и 2 раза записано число 0. Такой набор отвечает всем требованиям задачи.
Ответ: а) 44; б) отрицательных; в) 17.
Задача 3: На доске написано 35 различных натуральных чисел, каждое из которых либо чётное, либо его десятичная запись оканчивается на цифру 3. Сумма написанных чисел равна 1062.
а) Может ли на доске быть ровно 27 чётных чисел?
б) Могут ли ровно два числа на доске оканчиваться на 3?
в) Какое наименьшее количество чисел, оканчивающихся на 3, может быть на доске?
Решение:
а) Такой примерный перечень чисел на доске соответствует заданным условиям:
3, 13, 23, 33, 43, 53, 63, 73, 2, 4, 6,…,50, 52, 56
б) Пусть на доске написано ровно два числа, у которых последняя цифра 3. Тогда там записано 33 чётных числа. Их сумма:
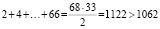
Это противоречит тому, что сумма написанных чисел равна 1062
в) Полагаем, что на доске записано n чисел, которые оканчиваются на 3, и (35 – n) из выписанных чётные. Тогда сумма чисел, которые оканчиваются на 3, равна
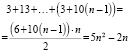
а сумма чётных:
2 + 4 + … + 2(35 – n) = = (35 – n)(36 – n) = n2-71 n + 1260.
Тогда из условия:
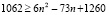
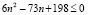
Решаем получившееся неравенство:
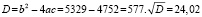
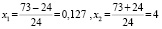
Получается, что n ≤ 0,126 или n ≥ 4,03. Отсюда, зная, что n – натуральное, получаем n ≥ 5. Наименьшее число чисел, оканчивающихся на 3, может быть только 5. И добавлено 30 чётных чисел, тогда сумма всех чисел нечётна. Значит, чисел, которые оканчиваются на 3, больше.чем пять, поскольку сумма по условию равна четному числу. Попробуем взять 6 чисел, с последней цифрой 3. Приведём пример, когда 6 чисел, оканчиваются на три, и 29 чётных чисел. Сумма их равна 1062. Получается такой список:
3, 13, 23, 33, 43, 53, 2, 4, ..., 54, 56, 82.
Ответ: а) да; б) нет; в) 6.
Задача 4: Маша и Наташа делали фотографии несколько дней подряд. В первый день Маша сделала m фотографий, а Наташа – n фотографий. В каждый следующий день каждая из девочек делала на одну фотографию больше, чем в предыдущий день. Известно, что Наташа за всё время сделала суммарно на 1173 фотографии больше, чем Маша, и что фотографировали они больше одного дня.
а) Могли ли они фотографировать в течение 17 дней?
б) Могли ли они фотографировать в течение 18 дней?
в) Какое наибольшее суммарное число фотографий могла сделать Наташа за все дни фотографирования, если известно, что в последний день Маша сделала меньше 45 фотографий?
Решение:
а) Если Маша сделала m фотографий в 1-й день, то за 17 дней она сфотографировала m + (m + 1) + (m + 2) + … + (m + 16) = 17m + 1 + 2 + … + 16 = 17m + 136 снимков.
Наташа, за 1-й день сделала n фотографий, тогда за оставшиеся 17 дней она сделала 17n + 136 кадров.
Найдем такие m и n, чтобы выполнялось равенство:
17n + 136 – 17m – 136 = 1173
17n – 17m = 1173
n – m = 69
Возьмем, к примеру, n = 70 и m = 1.
1. Если фотографировали девочки всего 18 дней, получается:
18n – 18m = 1173
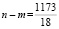
1173 на 18 не разделится, следовательно, выбрать такие n и m нельзя.
1. Допускаем, что девочки делали фотографии x дней. Тогда Маша сделала бы в последний день снимков
m + x – 1 < 45
m + x < 46
То есть 1 < x < 46. А согласно условию
nx – mx = 1173
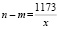
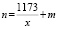
число x является делителем 1173. Тогда возможны только варианты: x = 23, 17 или 3. Вычисляем наибольшее число фотографий, которые могла сделать Маша. Получаем:
Для числа x = 3:
m + 3 < 46 → m < 43 → m = 42
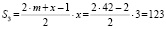
При x = 17:
m + 17 < 46 → m < 29 → m = 28
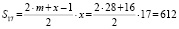
А при x = 23:
m + 23 < 46 → m < 23 → m = 22
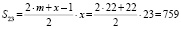
Самое большое количество снимков, которые сделала Наташа:
759 + 1173 = 1932.
Ответ: а) да; б) нет; в) 1932.
Задача 5: На доске написано 30 различных натуральных чисел, каждое из которых либо чётное, либо его десятичная запись оканчивается на цифру 7. Сумма написанных чисел равна 810.
а) Может ли на доске быть ровно 24 чётных числа?
б) Могут ли ровно два числа на доске оканчиваться на 7?
в) Какое наименьшее количество чисел, оканчивающихся на 7, может быть на доске?
Решение:
а) Да, например:
2 + 4 + … + 44 + 46 + 66 + 7 + 17 + 27 + 37 + + 47 + 57 =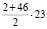 
+ 66 + 192 = 810
б) Пусть на доске ровно два числа, оканчивающихся на 7. Тогда на доске написано 28 четных чисел. Их сумма не меньше, чем:
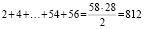
Это противоречит тому, что сумма равна 810, то есть на доске не может быть двух чисел, оканчивающихся на 7.
в) Заметим, что число 810 кратно двум, тогда и сумма чисел, оканчивающихся на 7, тоже кратна двум. Чтобы сумма нечетных чисел делилась на два, слагаемых должно быть четное количество. В пункте б) показано, что на доске не может быть два числа, оканчивающихся на 7, тогда наименьшее возможное количество таких чисел – 4.
Приведем пример, когда на доске написано четыре числа, оканчивающихся на 7:
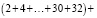
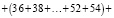
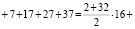
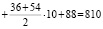
Ответ: а) да; б)нет; в) 4.
Задача 6: С натуральным числом производят следующую операцию: между каждыми двумя его соседними цифрами записывают сумму этих цифр (например, из числа 1923 получается число 110911253).
а) Приведите пример числа, из которого получается 4106137125
б) Может ли из какого–нибудь числа получиться число 27593118?
в) Какое наибольшее число, кратное 9, может получиться из трехзначного числа, в десятичной записи которого нет девяток?
Решение: а)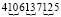 
, т.е. было число 4675.
б)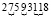 
вместо 9 должно быть 8, так что не может.
в) должно получиться наибольшее, а в записи нет 9. Значит первая цифра 8, и, т.е. в итоге получается 8168157
Ответ: а) 4675; б)нет; в) 8168157
Задача 7: На доске написано 100 различных натуральных чисел, сумма которых равна 5130
а) Может ли оказаться, что на доске написано число 240?
б) Может ли оказаться, что на доске нет числа 16?
в) Какое наименьшее количество чисел, кратных 16, может быть на доске?
Решение: а) Наименьшая сумма (1 + 99)/2·99 = 4950
4950 + 240 = 5190 > 5130
Не может. 240 + наименьшая сумма = число, которое больше 5130.
б) (1 + 100)/2·100 = 5050 – наименьшая сумма 100 чисел. (1 + 2 + .. + + 99 + 100) = 5050
5050 – 16 = 5034 – 99 чисел (1, 2..15, 17..100)
5130–5034 = 96 – это число уже было в последовательности, значит, не может оказаться, что на доске нет числа 16.
в)1 + 2 + .. + 99 + 180 = 5130
На 16 делятся: 16,32,48,64,80,96
заменим 96 на 100, а 180 на 176
80 на 101, а 176 на 155
64 на 102,а 155 на 117
48 на 103, а 117 на 62 (Мы не можем, замени 117 на 62, т.к. такое число уже есть, поэтому и 48 на 103 не меняем.)
У нас осталось 3 числа: 16, 32, 48
Ответ: а) нет, б) нет, в) 3
Задача 8: На доске написано 30 различных натуральных чисел, каждое из которых либо четное, либо его десятичная запись заканчивается на цифру 7. Сумма написанных чисел равна 810.
а) Может ли на доске быть ровно 24 четных числа?
б) Могут ли ровно два числа на доске оканчиваться на 7?
в) Какое наименьшее количество чисел, оканчивающихся на 7, может быть на доске?
x – чётное, y – заканчивается на 7
Решение: а) Да
24x + 6y = 810
y = 135–4x
Пусть x = 2
y = 127
То есть на доске 24 раза встречается число 2 и 6 раз 127.(один из вариантов написания чисел на доске)
Проверим равенство 24·2 + 6·127 = 810.
б) Да
28x + 2y = 810; 14x – y = 405
y = 405 – 14x
Пусть x = 2
y = 377
На доске написано 377, 377 и 28 двоек.
Проверим: 377 + 377 + 28·2 = 810
в) Если 0 считается, то он.
Если нет, то 2, т.к. на 7 оканчиваются нечётные числа, а два нечётных дают чётное число.
Ответ: а) да; б) да; в) 2
Задача 9: На доске написано 30 чисел. Каждое из них либо четное, либо десятичная запись числа оканчивается на 3. Их сумма равна 793.
а) может ли на доске быть ровно 23 чётных числа;
б) может ли только одно из чисел оканчиваться на 3;
в) какое наименьшее количество из этих чисел может оканчиваться на 3?
Поскольку понятие чётности и нечётности существует только для целых чисел, то указывать в ответе будем именно такие числа.
Решение: а) да, например, «–6» – 12 штук, « + 6» – 11 штук, «–3» – 2 штуки, « + 3» – 4 штуки, « + 793» – 1 штука.
б) да, например, «0» – 29 штук, « + 793» – 1 штука.
в) 793
Ответ: а) да; б) да; в) 793 [4].
Заключение
Решение задач по теории простых чисел Фробениуса – поистине обширная, многогранная область математики. Множество решений таких задач колоссально, и каждый подвид имеет свои особенности и свойства. Но на основании проведенных исследований было выяснено, что эти задачи не имеют единого алгоритма решения. Однако стоит отметить, что в зависимости от вида, они обладают определенным методом решения, а иногда могут быть решены разными способами. Теория простых чисел Фробениуса имеют за собой довольно большую историю. Этот раздел теории чисел смело можно назвать одним из самых любопытных разделов алгебры и математики в целом.
Теоретическая значимость исследования заключается в проведении классификации методов решения нестандартных задач из ЕГЭ, решаемых с применением теории чисел, представленные в таблице 1. Кроме основных методов, в работе рассмотрены и альтернативные методы (приложение А).
Практическая значимость состоит в том, что подробно рассмотренные в работе задачи могут быть использованы при проведении элективных курсов по математике в 10-11 классах ГБОУ СОШ № 5 «ОЦ» в г. Новокуйбышевск Самарской области (приложение Б). Также работа может быть интересна учащимся 5-11 классов, которые часто принимают участие в олимпиадах, а также ученикам 10-11 классов, заинтересованным в успешной сдаче ЕГЭ.
Таким образом, теорема Фробениуса – поистине обширная, многогранная область математики. Множество решений таких задач колоссально, и каждый подвид имеет свои особенности и свойства. Теория простых чисел Фробениуса имеют за собой довольно большую историю. Этот раздел теории чисел смело можно назвать одним из самых любопытных разделов алгебры и математики в целом.
Библиографическая ссылка
Чернецова И.Н. ПРИМЕНЕНИЕ ТЕОРЕМЫ ФРОБЕНИУСА ПРИ РЕШЕНИИ НЕСТАНДАРТНЫХ ЗАДАЧ ПО МАТЕМАТИКЕ // Международный школьный научный вестник. – 2019. – № 5-2. ;URL: https://school-herald.ru/ru/article/view?id=1186 (дата обращения: 21.12.2024).