Международный школьный научный вестник

Научный журнал для старшеклассников и учителей ISSN 2542-0372

Актуальность данного исследования определяется тем, что решение многих практических задач в области физики, техники и информационных технологий сводится к решению квадратных уравнений. В школьном курсе математики изучаются виды квадратных уравнений, способы их решения. Как правило, корни квадратного уравнения учащиеся находят с помощью формул корней квадратного уравнения или применяют теорему Виета и обратную ей теорему.

Проблема: отсутствие навыков решения квадратных уравнений различными способами у некоторых учащихся мешает им успешно подготовиться к итоговой аттестации по математике и математическим олимпиадам, дальнейшему обучению в профильном математическом классе.

Цель работы: изучение известных способов решения квадратных уравнений и выявление наиболее рациональных из них для практического применения.

Исходя из поставленной цели, в работе определены следующие задачи:

– изучить литературу и Интернет-ресурсы по данной теме;

– познакомиться с историческими фактами решения квадратных корней;

– описать различные способы решения квадратных уравнений и алгоритмы вычислений, сравнить степень сложности каждого из них;

– познакомить одноклассников со способами решения квадратных уравнений, которые не изучаются в школьной программе по математике.

Объект исследования – квадратные уравнения.

Предмет исследования – способы решения квадратных уравнений.

Гипотеза: кроме общеизвестных способов решения квадратных уравнений существуют другие способы решения, которые могут иметь практическое применение.

Методы исследования:

– библиографический метод (анализ литературы по теме исследования);

– метод классификации и метод качественного анализа.

Теоретическая значимость исследования состоит в систематизации способов решения квадратных уравнений и описании их алгоритмов.

Практическая значимость – предъявленный материал по данной теме и разработанная памятка «Способы решения квадратных уравнений» могут быть использованы для практического применения в учебном процессе.

Квадратное уравнение

Понятие квадратного уравнения

Определение 1. Квадратным уравнением называют уравнение вида

ах2 + bх + с = 0, где коэффициенты а, b и с – любые действительные числа, причём, а ≠ 0 [8, 143].

Многочлен ах2 + bх + с называют квадратным трёхчленом, где а – первый или старший коэффициент; b – второй или коэффициент при х, с – свободный член. Квадратное уравнение также называют уравнением второй степени, так как его левая часть есть многочлен второй степени.

Определение 2. Квадратное уравнение называют приведённым, если старший коэффициент равен 1; квадратное уравнение называют неприведённым, если старший коэффициент отличен от 1. х² + рх + q = 0 – стандартный вид приведённого квадратного уравнения [8, 143].

Кроме приведенных и неприведённых квадратных уравнений различают также полные и неполные уравнения.

Полное квадратное уравнение – это квадратное уравнение, в котором присутствуют все три слагаемых; иными словами, это уравнение, у которого коэффициенты b и с отличны от нуля.

Неполное квадратное уравнение – это уравнение, в котором присутствуют не все три слагаемых; иными словами, это уравнение, у которого хотя бы один из коэффициентов b и с равен нулю.

Определение 3. Корнем квадратного уравнения ах² + bх + с = 0 называют значение переменной х, при котором квадратный трехчлен ах² + bх + с обращается в нуль. Такое значение переменной х называют также корнем квадратного трехчлена.

В ходе исследования было выявлено, что современной науке известно много различных способов решения квадратного уравнения, начиная с методов математиков далекой древности (метода Евклида – при помощи деления отрезка в среднем и крайнем отношениях) и заканчивая способами решения уравнений сложных степеней из разделов высшей математики.

Исторические сведения о квадратных уравнениях.

Из истории квадратных уравнений

Вавилоняне писали клинописными значками на глиняных табличках, которые в немалом количестве дошли до наших дней (более 500000, из них около 400 связаны с математикой). Поэтому мы имеем довольно полное представление о математических достижениях учёных Вавилонского государства. Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила.

В древней Греции квадратные уравнения решались с помощью геометрических построений. Методы, которые не связывались с геометрией, впервые приводит Диофант Александрийский в III в. н.э. В своих книгах «Арифметика» он приводит примеры решения неполных квадратных уравнений. Его книги с описанием способов решения до нашего времени не сохранились [4, 21].

Квадратные уравнения решали и в Индии. Задачи на квадратные уравнения встречаются уже в астрономическом тракте «Ариабхаттиам», составленном в 499 г. индийским математиком и астрономом Ариабахаттой. Другой индийский ученый, Брахмагупта (VII в.), изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме: ах2 + bх = с, а > 0. В уравнении коэффициенты, кроме коэффициента а, могут быть отрицательными. Правило Брахмагупта по существу совпадает с современным правилом [4, 23]. Общее правило решения квадратных уравнений было сформировано немецким математиком М. Штифелем (1487 – 1567). Выводом формулы общего решения квадратных уравнений занимался Виет [4, 25]. Он же и вывел формулы зависимости корней уравнения от коэффициентов в 1591 году. После трудов нидерландского математика А. Жирара (1595 – 1632), а также Декарта и Ньютона способ решения квадратных уравнений приобрел современный вид.

В работе описаны различные способы решения квадратных уравнений. Среди них способы, выходящие за рамки школьной программы – способ, основанный на свойствах коэффициентов квадратного уравнения, решение уравнений способом «переброски», с помощью циркуля и линейки, а также с использованием номограммы и геометрический метод.

Cпособы решения квадратного уравнения

Разложение квадратного трехчлена уравнения на множители

С этим способом мы познакомились в школьном курсе алгебры 8 класса. Он основан на «способе группировки» при разложении многочленов на множители и позволяет достаточно быстро решать квадратное уравнение.

Вывод: способ не сложный и понятный, им может пользоваться любой учащийся.

Выделение полного квадрата

Решение квадратных уравнений выделением квадрата двучлена опирается на применение формулы сокращенного умножения: (a + b)2 = a2 + 2ab + b2 и (a–b)2 = a2 – 2ab + b2.

Вывод: способ выделения полного квадрата требует знания формул сокращенного умножения и хороших вычислительных навыков (в случае, если коэффициенты рациональные числа).

Применение формул корней квадратного уравнения

Используя выделение полного квадрата для квадратного трехчлена уравнения ах2 + bх + с = 0, а ? 0 мы получим формулы, с помощью которых найдем корни уравнения

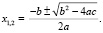
Формула позволяет найти корни любого квадратного уравнения, в том числе приведенного и неполного. При этом необходимо учитывать число корней в зависимости от дискриминанта D = b2– 4ac, D > 0, два разных корня; D = 0, один корень; D < 0, нет корней.

Известно, что кроме основной формулы корней квадратного уравнения существует формула, которая применяется при решении квадратного уравнения с чётным вторым коэффициентом, то есть b = 2k.

Решение уравнений с использованием теорем Виета

Любопытные соотношения между корнями квадратного уравнения и его коэффициентами впервые обнаружил французский математик Франсуа Виет (1540 – 1603), которые он описал в своей знаменитой теореме и обратной ей [4, 180]. Если х1 и х2 – корни уравнения, то х1 + х2 = – 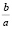, х1•х2 = 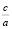(теорема Виета).

Для приведенного квадратного уравнения вида х2 + px + q = 0. Эти соотношения имеют вид: 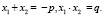По коэффициентам p и q можно предсказать знаки корней: а) если сводный член q приведенного уравнения положителен (q > 0), то уравнение имеет два одинаковых по знаку корня и это зависти от второго коэффициента p. Если р > 0, то оба корня отрицательны, если р < 0, то оба корня положительны;

б) если свободный член q уравнения отрицателен (q < 0), то уравнение имеет два различных по знаку корня, причем больший по модулю корень будет положителен, если p < 0, отрицателен, если p > 0.

Мы пришли к выводу, что рассмотренные выше способы решения уравнений имеют практическое применение только при твёрдом знании формул корней и теорем Виета. Немаловажную роль играют также хорошие вычислительные навыки учащихся.

Графическое решение квадратного уравнения

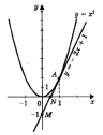
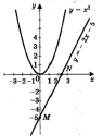
Если в уравнении ax2 + bx + c = 0, из левой части перенести второй и третий члены многочлена в правую часть, то получим: ax2 = – (bx + c). Рассмотрим две функции: y = ax2 и y = – (bx + c). График первой зависимости – парабола, проходящая через начало координат. График второй зависимости – прямая. Возможны следующие случаи взаимного расположения графиков функций: пересечение двух графиков, два графика касаются, два графика не имеют общих точек.

Рассмотрим три случая решений квадратных уравнений:

а) решим графически уравнение х2 – 3х – 4 = 0, (рис. 1, а). Ответ: х1 = – 1; х2 = 4.

б) уравнение х2 – 2х + 1 = 0, (рис. 1, б). Ответ: х = 1.

в) уравнение х2 – 2х + 5 = 0, (рис. 1, в).Ответ: корней нет.

Вывод: если строить параболу по точкам, то требуется много времени, и при этом степень точности получаемых результатов невелика.

Способ, основанный на свойствах коэффициентов квадратного уравнения

10. Если a + b + c = 0, то x1 = 1, x2 = .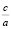

20. Если a – b + c = 0, то x1 = – 1, x2 = – ;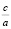

30. Рассмотрим уравнение вида

ах2 + (а2 + 1) х + a = 0; a ? 0

и найдем его корни

D = a4 + 2a2 + 1 – 4a2 = a4– 2a2 + 1 = (a2– 1)2,

x1,2 = =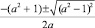

= .

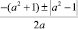Не нарушая общности можно считать, что перед нами квадратное уравнение с целыми коэффициентами (даже если бы коэффициенты были дробными, уравнение можно было бы свести к уравнению с целыми коэффициентами), т.е. если a?Z и тогда a2 – 1 > 0, а значит

x1 =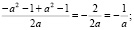

x2 = .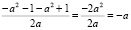

Ответ: x1 = – 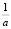; x2 = – a.

Исследуя взаимосвязь между коэффициентами квадратного уравнения и его корнями, мы заметили, что существуют квадратные уравнения, корни которых можно найти благодаря пониманию описанных гипотез.

Способ «переброски» первого коэффициента

Рассмотрим квадратное уравнение ах2 + bх + с = 0, где а ? 0. Домножим обе его части на а, получаем уравнение а2х2 + аbх + ас = 0. Пусть ах = у, откуда х = у/а. Уравнение у2 + by + ас = 0 равносильно данному. Его корни у1 и у2 найдем с помощью теоремы Виета. Окончательно получаем х2 = у1/а и х1 = у2/а. При этом способе коэффициент a умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски».

Вывод: способ «переброски» привлекает своеобразным подходом в описании алгоритма решения уравнения. Вместе с тем данный способ вызывает затруднения в его понимании.

Решение квадратных уравнений с помощью номограммы

Это старый и незаслуженно забытый способ решения квадратных уравнений, о котором рассказывается в Таблице XXII Четырехзначных математических таблиц, автор В.М. Брадис. Номограмма позволяет, не решая квадратного уравнения z2 + рz + q = 0, по его коэффициентам определить корни уравнения [2, 83].

Алгоритм решения и практическая часть решения уравнений описаны ниже.

Решение квадратных уравнений с помощью номограммы

Номограмма (от греческого «nomos» – закон и …грамма), графическое представление функции от нескольких переменных, позволяющее с помощью простых геометрических операций (например, прикладывание линейки) исследовать функциональные зависимости без вычислений. Например, решать квадратное уравнение без применения формул.

Рассмотрим уравнение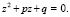

Криволинейная шкала номограммы построена по формуле 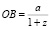, 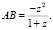Полагая ОС = р, ED = q, ОЕ = а, из подобия треугольников САН и CDF получим пропорцию 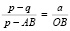. После подстановок и упрощений вытекает уравнение 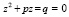, причем буква z означает метку любой точки криволинейной шкалы (рис. 2).

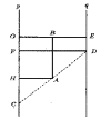
Рис. 2

Примеры:

1) Для уравнения z2 – 9z + 8 = 0 номограмма дает корни z1 = 8 и z2 = 1.

2) Решим с уравнение 2z2 – 9z + 2 = 0. Разделим коэффициенты этого уравнения на 2, получим уравнение z2 – 4,5z + 1 = 0. Номограмма дает корни z1 = 4 и z2 = 0,5 (рис. 3).

3) Для уравнения х2 + 5х – 6 = 0 номограмма даёт только положительный корень х1 = 1, а отрицательный находим так: х2 = – b – х1 = -5-1 = – 6.

4) Для уравнения х2 – 2х – 8 = 0, х1 = 4, а х2 = –b – х1 = 2 – 4 = –2.

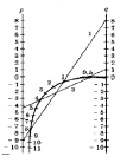
Рис. 3

Решение квадратных уравнений с помощью циркуля и линейки

Решим квадратное уравнение ах2 + bх + с = 0 с помощью циркуля и линейки (рис. 4). Допустим, что искомая окружность пересекает ось абсцисс в точках В(х1; 0) и D(х2; 0), где х1 и х2 – корни уравнения ах2 + bх + с = 0, и проходит через точки А(0; 1) и С(0;c/a) на оси ординат. По теореме о секущих имеем OB•OD = OA•OC, отсюда OC = OB•OD/OA = х1,•х2/1 = c/a. Центр окружности находится в точке пересечения перпендикуляров SF и SK, восстановленных в серединах хорд AC и BD, 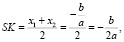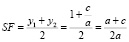[10, 34].

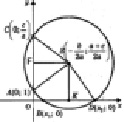
Рис. 4

Итак:

1) построим точки 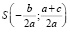(центр окружности) и A(0; 1);

2) проведем окружность радиусом SA;

3) абсциссы точек пересечения этой окружности с осью ох являются корнями исходного квадратного уравнения. При этом возможны три случая:

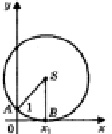
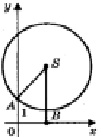
а) два решения (рис. 5, а);

б) одно решение (рис. 5, б);

в) нет решений (рис. 5, в).

Решение квадратных уравнений с помощью циркуля и линейки

1. Построим точки S 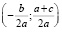(центр окружности) и A(0; 1);

2) проведем окружность с радиусом SA;

3) абсциссы точек пересечения этой окружности с осью ох являются корнями исходного квадратного уравнения (рис. 6). При этом возможны три случая.

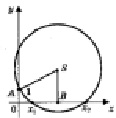
а)

б)

в)

Рис. 5

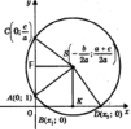
Рис. 6

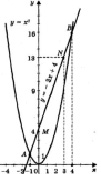
а) б) в)

Рис. 1. Графическое решение квадратного уравнения

а) б) в)

г) д)

Рис. 7

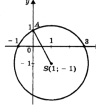
Пример 1. Решим уравнение х2 – 2х – 3 = 0 (рис. 7, а).

Определим координаты точки центра окружности по формулам:

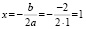и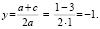

Проведем окружность радиуса SA, где А (0; 1).

Ответ: х1 = – 1; х2 = 3, уравнение имеет два решения.

Пример 2. Решим уравнение х2 + 4х + 4 = 0 (рис. 7, г).

Определим координаты точки центра окружности по формулам:

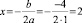и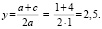

Проведем окружность радиуса SA, где А (0;1).

Ответ: х1 = 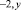равнение имеет одно решение.

Пример 3. Решим уравнение х2 – 2х + 3 = 0 (рис. 7, д).

Определим координаты точки центра окружности по формулам:

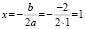и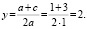

Проведем окружность радиуса SA, где А (0; 1).

Ответ: уравнение не имеет решения.

Вывод: очевидно, что этот красивый способ практически не применяется из-за геометрических построений и последующей проверки результатов решения.

Геометрический способ решения квадратных уравнений

В древности, когда геометрия была более развита, чем алгебра, квадратные уравнения решали не алгебраически, а геометрически. Вот пример из «Алгебры» ал – Хорезми: х2 + 10х = 39. На сторонах квадрата со стороной х строятся прямоугольники так, что другая сторона каждого из них равна 2,5. Площадь каждого прямоугольника равна 2,5х. Полученную фигуру дополняют до нового квадрата, достраивая в углах четыре равных квадрата, сторона каждого из них равна 2,5, а площадь 6,25. Площадь квадрата можно представить как сумму площадей: первоначального х2, четырёх прямоугольников 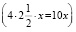, т.е. S = x2 + 10x + 25.

Из геометрического метода нахождения квадратных корней вытекает любопытнейший способ решения уравнений, основанный на выполнении различных действий с отрезками и позаимствованный из книги «Геометрия» великого французского ученого Рене Декарта (1596-1650).

Геометрический способ решения квадратного уравнения

Пусть надо решить, уравнение х2 + 10х + 9 = 0. Выполним следующее построение.

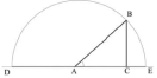
Рис. 8

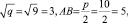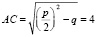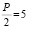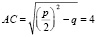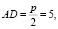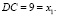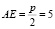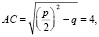Сначала по катету и гипотенузе ВС = построим прямоугольный треугольник. Заметим, что . Радиусом, равным проведем окружность с центром в точке A. Она пересечет продолжение катета AC в двух точках, которые обозначим D и E. Отрезок DC составлен из и, т.е. Отрезок ж CE есть разность отрезков и т.е. отрезок 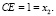Отрезок BC есть корень квадратный из q, произведения отрезков х1 и х2.

Результаты исследования и их обсуждение

В ходе исследовательской работы был проведен опрос на предмет применения различных способов решения квадратного уравнения, которыми владеют одноклассники и учащиеся девятых классов МБОУ «СОШ № 9». С этой целью учащимся было предложено решить квадратные уравнения. Результаты проверки показали, что большая часть опрошенных находили корни уравнения с помощью: общей формулы корней. Таких учащихся – 82 %. С помощью теоремы Виета корни уравнения нашли – 6 % учащихся, а другими способами –12 % .

Демонстрация результатов исследовательской работы, т.е. способов решения уравнений, не изучаемых в школьной программе по математике, заинтересовала учащихся, а их практическое применение выявило недостатки и преимущества каждого из способов.

Была дана характеристика алгоритмов решения по таким критериям, как трудоёмкость и точность вычислений, а также насколько удобен тот или другой метод, математически красив и практичен. По результатам практической работы каждый из участников эксперимента выставил условную отметку, и было установлено, что наиболее сложными для школьников оказались следующие способы: разложение левой части уравнения на множители, метод выделения полного квадрата. Наиболее доступными для учащихся в понимании алгоритмов решения были способы: решение квадратных уравнений по формуле корней и решение уравнений с использованием теорем Виета (для уравнений приведенного вида), применение свойств коэффициентов квадратного уравнения.

Решение квадратных уравнений с помощью циркуля и линейки, геометрический способ решения квадратных уравнений вызвали интерес со стороны одноклассников, но необходимо отметить, что широкого практического применения они не имеют.

Очень необычными способами оказались: решение уравнений с помощью номограммы и решение уравнений способом «переброски».

Заключение

Изучив учебную и научную литературу, Интернет-ресурсы в молодежных образовательных форумах по теме: «Способы решения квадратных уравнений» мы выяснили, что современной науке известно много способов решения квадратных уравнений. Следует отметить, что некоторая часть изученных способов не входит в школьный курс, так как относится к разделу прикладной математики. В ходе работы было отмечено, что не все способы удобны для решения, но каждый из них уникален.

Мы считаем, что смогли выполнить поставленную перед собой цель работы, так как:

1) изучили, описали алгоритмы вычислений и проверили на практике 10 способов решения квадратных уравнений, (всего было найдено 11);

2) представили результаты исследования одноклассникам с целью знакомства со способами решения квадратных уравнений и выявления на их взгляд наиболее эффективного способа.

Итогом нашей работы является образовательный продукт – создана памятка по теме: «Способы решения квадратного уравнения».

Практическая значимость данной работы заключается, в возможности использования результатов исследования в практике организации самостоятельной работы учащихся при решении уравнений на уроках, факультативных занятиях и экзаменах в формате ОГЭ по математике.