Введение
Структура Контрольно-измерительных материалов ОГЭ отвечает цели построения системы дифференцированного обучения математике в современной школе. Дифференциация обучения направлена на решение двух задач: формирования у всех обучающихся базовой математической подготовки, составляющей функциональную основу общего образования, и одновременного создания условий, способствующих получению частью обучающихся подготовки повышенного уровня, достаточной для активного использования математики во время дальнейшего обучения, прежде всего при изучении её в средней школе на профильном уровне.
Чтобы быть зачисленным в профильный 10 класс на базе нашего учебного учреждения, необходимо сдать успешно экзамены по итогу 9-го класса. Успешно для меня – это значит на «отлично». Критерии оценивания экзамена по математике таковы: чтобы получить отметку «отлично», необходимо набрать минимум 22 балла. Это становится возможным лишь тогда, когда выпускник приступает к решению заданий с развёрнутым ответом с №20 - №25.
Со слов сверстников, я знаю, что не все педагоги, работающие в общеобразовательных школах, рассматривают с обучающимися задания повышенного уровня сложности, анализ типичных ошибок, которые допускают выпускники прошлых лет.
Мой вклад в решение данного проблемного вопроса заключается в том, что я предлагаю своим ровесникам, на основании моей работы, рассмотреть типичные ошибки выпускников, и самостоятельно закрепить материал, подготовиться к экзамену с помощью предложенных заданий. Мной были проанализированы КИМы с 2016-2019 годы.
Обзор литературы
Вопрос типичных ошибок, которые допускают выпускники, в тех или иных заданиях, особенно 2 части, рассматривается педагогами на совещаниях по итогам ГИА. Я не нашла ни одной исследовательской работы по данному направлению, которая была бы предложена учащимися. В основном данный проблемный вопрос представлен в виде педагогических статей.
По рекомендации своего руководителя основным источником исследования стали «Методические рекомендации результатов государственной итоговой аттестации в форме основного государственного экзамена по математике в Иркутской области», которые издаются Государственным автономным учреждением дополнительного профессионального образования Иркутской области «Институт развития образования Иркутской области».
Цель
Анализ типичных ошибок выпускников в решении задания №20 (2 часть) по теме «Уравнения».
Методы исследования
1.Поисковый.
2. Анализ, синтез (отбор необходимой информации, обобщение)
3.Практический
Результаты исследования
Спецификация контрольно измерительных материалов ОГЭ по математике.
Я рассмотрела спецификацию контрольных измерительных материалов для проведения ОГЭ. И сделала вывод, что задание №20 проверяет умение учащегося выполнять преобразования алгебраических выражений, решать уравнения. Задание №20 относится к повышенному уровню сложности и оценивается на 2 балла. Задания, оцениваемые в 2 балла, считаются выполненными верно, если обучающийся выбрал правильный путь решения, из письменной записи решения понятен ход его рассуждений, получен верный ответ. В этом случае ему выставляется полный балл, соответствующий данному заданию. Если в решении допущена ошибка, не имеющая принципиального характера и не влияющая на общую правильность хода решения, то участнику выставляется 1 балл.
Задание №20 подразделяется на:
-алгебраические выражения;
-уравнения;
-неравенства;
-системы неравенств;
-системы уравнений.
На данном этапе мной рассмотрены и представлены в работе:
Уравнения:
· Иррациональные.
· Дробно-рациональные.
· Уравнения, приводимые к квадратным.
· Применение свойств при решении уравнений.
Таблица 1
Основная статистика по выполнению задания №20 учащимися 9-х классов Иркутской области.
|
№ задания |
Содержание задания |
Процент участников, набравших максимальный балл по заданию |
|||
|
2016 |
2017 |
2018 |
2019 |
||
|
21 * |
Решить уравнение или систему уравнений |
6,4 |
21,1 |
10,6 |
14,8 |
*До 2020 года задание №20 значилось под №21. Изменения произошли в контрольно-измерительных материалах в 2020-2021 учебном году.
Приведённая статистика говорит о том, что в среднем лишь 13% выпускников справляются с заданием №20. [3:19]
Содержание задания №20 по годам. Типичные ошибки выпускников.
2016 год
Решите уравнение:
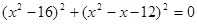
Поскольку приём использования в решении уравнений свойств отрабатывается в школе редко, с заданием справились лишь 6,4% учащихся Иркутской области.
2017 год
Решите уравнение:
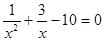
Типичные ошибки выпускников:
1.Вычислительные ошибки
2.Ошибки в формуле нахождения корней квадратного уравнения
3.Распостранённая ошибка в представлении ответа. Множество из двух корней уравнения описывалось как упорядоченная пара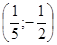 
, что является ошибкой в математической символике
4.Обучающиеся записывали корни в виде десятичных дробей и отбрасывали из ответа те из них, которые имели ненулевой период.
О критериях оценивания:
Решение, в котором была допущена вычислительная ошибка, но с ее учетом доведенное до конца, оценивалось в 1 балл.
Подчеркну, что ошибка в формуле нахождения корней квадратного уравнения не является вычислительной, и за ее допущение ставится 0 баллов.
Правильное решение с ошибкой в форме представления ответа – 1 балл.
Появление лишних корней в ответе в результате логической (не вычислительной) ошибки – 0 баллов.[1:15]
2018 год
Решите уравнение:
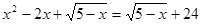
Типичные ошибки выпускников:
1) Основные ошибки в решении задачи 21 связаны с областью допустимых значений переменной, входящей в уравнение. Ошибка, как правило, заключалась либо в неэквивалентном преобразовании уравнения, произведенном без учета ограничения на область допустимых значений переменной, либо в неправильном определении (возможно, описании) области допустимых значений. Ошибки такого рода не относятся к вычислительным. Решение в таком случае оценивается в 0 баллов.
2) Вычислительные ошибки.
О критериях оценивания:
Решение, в котором была допущена вычислительная ошибка, но с ее
учетом доведенное до конца, оценивалось в 1 балл.
Подчеркну, что ошибка в определении области допустимых значений переменной не является вычислительной и за ее допущение ставится 0 баллов.
Появление лишних корней в ответе в результате логической (не вычислительной) ошибки – 0 баллов. [2:15]
Рисунок 1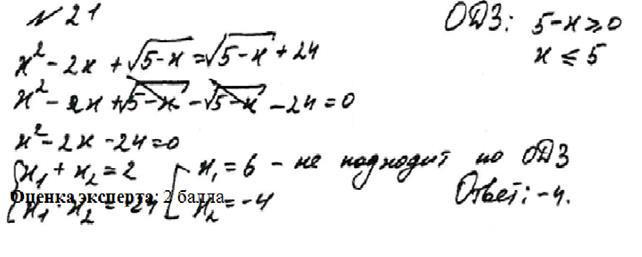
Вывод: данное уравнение решено верно. Обучающийся получил максимальное количество баллов.
Рисунок 2
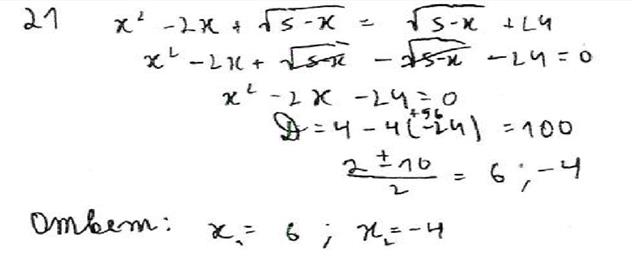
Вывод: в данном примере решения уравнения учащийся не определил ОДЗ и не учёл его при ответе. Оценка эксперта 0 баллов.
Рисунок 3
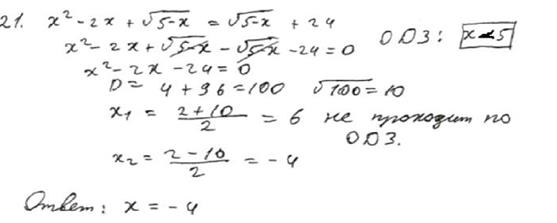
Вывод: здесь учащимся определена область допустимых значений, но неправильно: упущен случай равенства 5. Оценка эксперта 0 баллов.
2019 год
Решите уравнение:
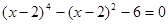
Типичные ошибки выпускников:
1.Вычислительные ошибки
2.Второй класс ошибок касается применения метода введения вспомогательной неизвестной при решении уравнения. [3:20]
Рисунок 4
Вывод: уравнение выпускником решено верно. Оценка эксперта 2 балла.
Банк заданий №20
Тщательно разобравшись в решении новых для меня уравнений, сделав анализ типичных ошибок выпускников, предлагаю небольшой банк заданий, который поможет моим сверстникам отработать задание №20.
Иррациональные уравнения (2019 год)
Решите уравнение: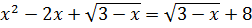 
Решение:
Поскольку подкоренное выражение не может быть меньше нуля, по свойству арифметического корня, область допустимых значений ограничивается выражением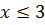 
значит,
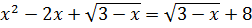ОДЗ:
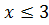
при уничтожении корней получаем:
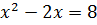
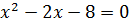решаем квадратное уравнение и получаем корни:
.
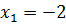
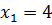Решением искомого уравнения является только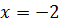 
, так как 
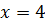не входит в область допустимых значений.
Ответ: .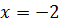
Решите уравнения самостоятельно:
a)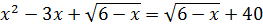 
(Ответ: 
);
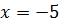b)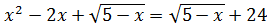
(Ответ: 
);
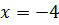c)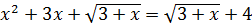 
(Ответ:
);
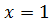d)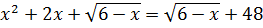 
(Ответ: 
).
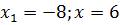Применение свойств при решении уравнений (2016 год)
Решите уравнение: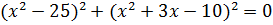 
.
Решение:
Квадрат любого числа неотрицателен. Сумма двух неотрицательных чисел равна нулю, только если они оба равны нулю. Получаем систему уравнений:
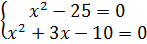
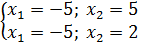
Так как системе удовлетворяет только 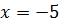, он и будет являться ответом.
Ответ: .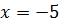
Решите уравнения самостоятельно:
a)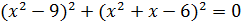 
(Ответ: 
;
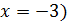b)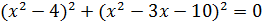 
(Ответ: 
;
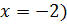c)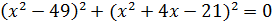 
(Ответ: 
;
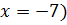d)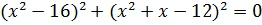 
(Ответ: 
.
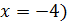Дробно-рациональные уравнения (2017 год)
Решите уравнение: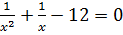 
Решение:
Так как на ноль делить нельзя, обозначаем область допустимых значений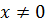 
и решаем:
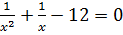ОДЗ: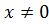
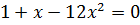
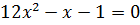
Решением через дискриминант получаем:
.
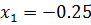
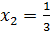Сверим корни с ОДЗ, не входят. Соответственно в ответе записываем оба корня.
Ответ: ; .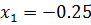
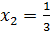Второй способ: замена переменной
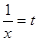
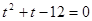, отсюда имеем, 
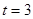и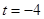 
, а значит ответ: ; .
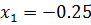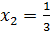Второй способ решения был предложен составителями экзаменационных материалов. Его применяет подавляющее большинство обучающихся.
Решите уравнения самостоятельно:
a)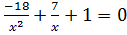 
(Ответ: 
);
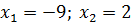b)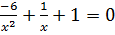 
(Ответ: 
);
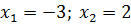c)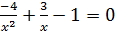 
(Ответ: 
;
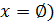d)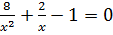 
(Ответ: 
).
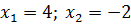Библиографическая ссылка
Беляева Е.Р. АНАЛИЗ ТИПИЧНЫХ ОШИБОК В РЕШЕНИИ УРАВНЕНИЙ, ПРЕДЛАГАЕМЫХ В КОНТРОЛЬНО-ИЗМЕРИТЕЛЬНЫХ МАТЕРИАЛАХ ОГЭ. ЗАДАНИЕ №20. МАТЕМАТИКА // Международный школьный научный вестник. – 2021. – № 2. ;URL: https://school-herald.ru/ru/article/view?id=1423 (дата обращения: 03.12.2024).