ВВЕДЕНИЕ
Цель: создать пособие по решению уравнений и неравенств различного вида, встречающихся в ОГЭ.
Задачи: 1) изучить теоретический материал по решению уравнений и неравенств;
2) подобрать уравнения и неравенства, встречающиеся в ОГЭ;
3) решить их;
4) собрать уравнения, неравенства и их решения в сборник.
Актуальность: Экзамен по математике является обязательным при прохождении государственной итоговой аттестации по программам основного общего образования, а в текстах ОГЭ в заданиях 1-ой и 2-ой частей присутствуют уравнения и неравенства различных степеней.
Проблема: решение уравнений и неравенств не всем даётся легко, но для написания ОГЭ оно обязательно.
Этапы работы:
1) Первый этап – исследовательский. (октябрь-декабрь 2020 г)
Результатом этого этапа является сбор, анализ и обобщение теоретического материала по решению уравнений и неравенств
2) Второй этап – практический (декабрь 2020-июнь 2021 гг)
Результатом этого этапа является поиск уравнений и неравенств, встречающихся в ОГЭ, и их решение.
3) Третий этап – организационный (июль 2021 г)
Результатом этого этапа является составление сборника по решению уравнений и неравенств, встречающихся в ОГЭ.
4) Четвёртый этап – подведение итогов (август 2021 г)
Результатом этого этапа является создание письменной работы и презентация проекта.
КРАТКИЙ ОБЗОР ЛИТЕРАТУРЫ
Проблема разработана в сборнике по подготовке к ОГЭ по математике Ф.Ф. Лысенко. Мой сборник будет отличаться, тем, что, во-первых, имеет более узкую направленность, а во-вторых, в нём описаны нестандартные способы решения уравнений и неравенств, которые не встречаются в школьной программе, но значительно упрощают работу над некоторыми выражениями.
МЕТОДЫ ИССЛЕДОВАНИЯ
Методы: анализ, сравнение.
Материально-техническое обеспечение: Различные пособия по решению уравнений, пособия для ОГЭ, сборники задач ОГЭ; принтер; компьютер с выходом в Интернет; ручка; карандаш; тетрадь; черновик.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
1. Стандартные и нестандартные способы решения уравнений и неравенств
1.1. Решение уравнений. Стандартные способы.
Рассмотрим некоторые наиболее часто встречаемые виды и способы решения уравнений, указанные в сборнике по подготовке к ОГЭ за 2021 Лысенко Ф. [1].
Со стандартными способами решения уравнений многие из нас знакомы. Главный их принцип – это перенос слагаемых с переменной в одну часть уравнения, без переменной – в другую (прим.: для уравнений первой степени); или разложение уравнения на множители (прим.: уравнения степени больше 1). Напомним, какие способы разложения на множители применяют:
1) Вынесение общего множителя за скобки
2) Способ группировки
3) Формулы сокращённого умножения
4) Разложение на множители квадратного трёхчлена (ax2+bx+c= a(x-x1)(x-x2), где x1 и x2 – корни уравнения ax2+bx+c=0).
Также стоит упомянуть свойство коэффициентов (Если a+b+c=0, то x1=1, x2=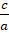
; Если a+c=b, то x1=-1, x2=
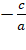) и теорему Виета (Если x1 и x2 – корни квадратного уравнения ax2+bx+c=0, то x1+x2=
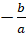, x1*x2=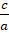), которые используются для решения квадратных уравнений.
Следует отметить, что в дробно-рациональных уравнениях нужно также находить корни, которые будут обращать знаменатель в ноль, чтобы позже исключить их (т.к. на 0 делить нельзя).
1.2. Решение неравенств. Стандартные способы.
Решение неравенства в своём начальном виде мало чем отличается от решения уравнения. Для решения неравенства первой степени нам нужно найти минимальное/максимальное значение x.
Для решения неравенств со степенью больше 1 применяется метод интервалов. Метод интервалов заключается в том, чтобы прировнять неравенство к нулю, найти корни этого выражения, разложить многочлен на множители, отметить их на числовой прямой, выяснить, какие знаки имеет многочлен в полученных интервалах и далее соотнести их со знаком самого неравенства.
2. Решение уравнений и неравенств. Нестандартные способы.
Следует заметить, что при решении уравнений и неравенств чаще всего применяют способы разложения на множители, особенно, если уравнение или неравенство содержат высокую степень.
Нестандартные же способы решения уравнений и неравенств, хотя и обычно связаны с разложением на множители, редко проходятся в школе на базовом уровне, их можно встретить лишь в углублённом изучении алгебры, и то не всегда. Но надо сказать, что они облегчают решение уравнений. Приведём несколько таких способов.
2.1. Теорема Безу.
Согласно учебнику по алгебре с углублённым изучением математики для 9 класса Макарычева Ю.Н. [1] данная теорема звучит так:
Если число α* является корнем многочлена P(x), имеющего степень n, то этот многочлен можно представить в виде:
P(x)=(x-α)*Q(x),
где Q(x) – многочлен степени n-1, получающийся при делении P(x) на (x-α).
*Важно отметить, что число α должно принадлежать множеству натуральных чисел.
Также есть вторая часть Теоремы Безу, которая звучит так:
Если число α является корнем уравнения, содержащего многочлен, то α – делитель свободного члена.
Или:
Если дробь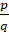 
является корнем уравнения, содержащего многочлен, то p – делитель свободного члена, а q – делитель старшего коэффициента.
2.2. Схема Горнера.
Для более простого перехода к нахождению корней уравнения можно воспользоваться схемой Горнера.
В её действии легче разобраться на примере, что сейчас мы и сделаем.
Пример №1. Разложим выражение на множители:
3x3-4x2-17x+6
По теореме Безу можно сделать вывод, что целые корни выражения находятся среди чисел -1;1;-2;2;-3;3;-6;6 (делители свободного члена). Числа 1 и (-1) можно проверить устно, подставив их в уравнение (по свойству коэффициентов):
3-4-17+6≠0 (подставили 1)
(-3)-4+17+6≠0 (подставили (-1))
Продолжаем проверять предполагаемые корни.
Вот тут себя и проявляет схема Горнера.
Этот вид решения уравнений и неравенств оформляется в виде таблицы, где в заглавиях столбцов находятся все коэффициенты выражения (вместе с их знаками!), а в заглавиях строк – предполагаемые корни:
|
|
3 |
-4 |
-17 |
6 |
|
-2 |
|
|
|
|
Сделав все вышеобозначенные приготовления, можно начать проверку. Сначала во вторую строку второго столбца сносим старший коэффициент:
|
|
3 |
-4 |
-17 |
6 |
|
-2 |
3 |
|
|
|
Далее мы перемножаем предполагаемый корень и старший коэффициент, а полученное число прибавляем к следующему в очереди коэффициенту выражения:
|
|
3 |
-4 |
-17 |
6 |
|
-2 |
3 |
(-2)*3-4=10 |
|
|
Проводим те же операции с получаемыми числами до конца строки. Если в конечной ячейке получился ноль – то проверяемое число является корнем уравнения. Вернёмся к нашей таблице:
|
|
3 |
-4 |
-17 |
6 |
|
-2 |
3 |
10 |
3 |
0 |
Как видите, число 2 – подходит нам. Можно продолжить проверять выведенные раньше числа (предполагаемые корни), а можно обратить внимание на другие числа, полученные в результате нашей проверки. Дело в том, что, если мы поделим уравнение 3x3-4x2-17x+6 на выражение x-2 (снова возвращаемся к теореме Безу), то получим такое выражение:
3x2+10x+3,
чьи коэффициенты соответствуют полученным в таблице числам. Исходя из этого, можно найти делители свободного члена нового выражения (1;-1;3;-3) и проверить их в качестве корней. Ранее мы выяснили, что числа 1 и (-1) не подходят, поэтому нам остаются только 3 и (-3). Проверим 3:
|
|
3 |
-4 |
-17 |
6 |
|
-2 |
3 |
10 |
3 |
0 |
|
3 |
3 |
-1 |
0 |
|
Число подошло, и мы получили выражение 3x-1, которое имеет первую степень, поэтому дальше разложения попросту не будет.
Ответ: 3x3-4x2-17x+6=(x+2)(x-3)(3x-1)
ПРАКТИЧЕСКАЯ ЧАСТЬ
Работа над проектом
Продуктом моего проекта стал сборник по решению уравнений и неравенств, встречающихся в ОГЭ. Его создание можно разделить на несколько различных этапов, в процессе которых я выяснила много нового и освежила старые знания на тему решения уравнений и неравенств.
1. Поиск материала
Материалом для моего проекта являются уравнения и неравенства, которые я находила в различных источниках.
Для начала я прорешала все задания на данную тему в сборнике «Математика. Подготовка к ОГЭ-2020» под редакцией Ф.Ф. Лысенко и С.О. Иванова. Этих заданий мне показалось недостаточно, тем более что данное пособие предназначено для подготовки к ОГЭ прошлого года, а данный экзамен, как и многие другие, каждый год даже пусть и незначительно, но меняет свою структуру.
Поэтому я зашла на два сайта – Решу ОГЭ и ФИПИ. На первом сайте (Решу ОГЭ) я открыла «Каталог заданий», нашла разделы, связанные с уравнениями и неравенствами и прорешала их. Также на данном сайте я просматривала сами варианты, чтобы выявить определённую динамику в заданиях – какие виды уравнений и неравенств действительно встречаются в ОГЭ. Благодаря последнему я поняла, что в ОГЭ 2021 встречаются такие задания, связанные с темой моего проекта:
· Задание 9 (1-ая часть ОГЭ); в нём даются уравнения, причём таких видов: линейные, квадратные, дробно-рациональные и системы уравнений с 2-мя неизвестными;
· Задание 13 (1-ая часть ОГЭ); в данном задании встречаются линейные, квадратные неравенства и системы неравенств с 1-ой переменной;
· Задание 20 (2-ая часть ОГЭ); здесь даются системы уравнений с 2-мя неизвестными, уравнения со степенью больше 2-х, квадратные и дробно-рациональные неравенства и системы неравенств. Следует отметить, что уравнения и неравенства в данном задании сложнее, чем те, что даются в 9-ом и 13-ом номерах. Это объясняется просто: 2-ая часть ОГЭ всегда сложнее 1-ой.
На ФИПИ я открыла раздел «Банк заданий» и рассмотрела подраздел «Уравнения и неравенства». На этом сайте выбора было значительно больше, чем на Решу ОГЭ, поэтому достаточное количество примеров и заданий в моём сборнике основано на том, что я нашла на ФИПИ.
Также я искала различные уравнения и неравенства на других сайтах (см. Список литературы и интернет-ресурсов).
2. Виды и типы уравнений и неравенств, которые я включила в свой сборник и их решения.
Мой сборник разделён на 2 части: одна касается уравнений, а вторая – неравенств. В 1-ую часть включены такие виды уравнений:
§ Линейные уравнения;
§ Квадратные уравнения;
§ Дробно-рациональные уравнения;
§ Системы уравнений с 2-мя переменными;
§ Уравнения со степенью больше 2-х.
Во 2-ую часть входят такие виды неравенств, как:
§ Линейные неравенства;
§ Квадратные неравенства;
§ Дробно-рациональные неравенства;
§ Системы неравенств с 1-ой переменной.
Каждый из этих видов можно разделить на определённые типы, которые имеют различные способы решения. Чтобы понять, как я решала задания в моём сборнике, предлагаю разобрать эти типы уравнений и неравенств.
ЗАКЛЮЧЕНИЕ
Выводы:
Думаю, я достигла поставленной цели и полностью решила выделенные мною задачи.
Мне удалось:
- пополнить свои знания в области решения уравнений и неравенств;
- научиться нестандартным способам решения уравнений и неравенств;
- подобрать уравнения и неравенства, встречающиеся в ОГЭ и решить их;с
- смоделировать структуру сборника по решению уравнений и неравенств;
- собрать уравнения, неравенства и их решения в удобный и практичный сборник.
Практическим результатом данной работы стало создание Пособия по решению уравнений и неравенств для подготовки к ОГЭ.
С точки зрения технической реализации, сборник удобен в использовании, так как имеет чёткую структуру и оглавление, причём к каждой теме подобраны примеры заданий и их решения и уравнения или неравенства для самостоятельного разбора.
В настоящий момент, доработка пособия продолжается, поскольку ОГЭ меняется каждый год, в результате чего, следует добавлять новые виды уравнений и неравенств и их решения.
Перспективы проекта:
1. Добавить новый материал для ОГЭ будущих лет
2. Доработать дизайн сборника
Библиографическая ссылка
Акишина С.А. РЕШЕНИЕ УРАВНЕНИЙ И НЕРАВЕНСТВ РАЗЛИЧНОГО ВИДА ДЛЯ ПОДГОТОВКИ К ОГЭ // Международный школьный научный вестник. – 2022. – № 3. ;URL: https://school-herald.ru/ru/article/view?id=1525 (дата обращения: 21.11.2024).