Международный школьный научный вестник

Научный журнал для старшеклассников и учителей ISSN 2542-0372

Введение

На языке алгебры формальные модели записываются с помощью уравнений, точное решение которых основывается на поиске равносильных преобразований алгебраических выражений, позволяющих выразить переменную величину с помощью формулы.

Точные решения существуют только для некоторых уравнений определённого вида (линейные, квадратные, тригонометрические и др.), поэтому для большинства уравнений приходится использовать методы приближённого решения с заданной точностью (графические или численные) [2].

Цель данной работы заключается в том, чтобы получить дополнительные знания и навыки по этой теме.

Задача состоят в том, чтобы подобрать соответствующий материал с последующей систематизацией, обобщением и иллюстрацией текста, а также практического решения конкретной задачи на языке объектно-ориентированного программирования Python и в табличном процессоре Microsoft Excel 2010 с использованием построения графика на основании составленной таблицы, языка Visual Basic for Applications (VBA) и надстройки Поиск решения.

Методы решения математических задач с заданной точностью

Графические методы решения

Построение графиков функций может использоваться для грубо приближённого решения уравнений. Для уравнений вида f(x) = 0, где f(x) – некоторая непрерывная функция, корень или (корни) этого уравнения являются точкой или (точками) пересечения графика функции с осью X.

Графическое решение таких уравнений можно осуществить путём построения компьютерных моделей:

· построением графика функции в системе объектно-ориентированного программирования Python.

· в табличном процессоре Microsoft Excel 2010 путём построения диаграммы типа График [2].

Численные методы

Для решения уравнений с заданной точностью можно применить разработанные в вычислительной математике численные методы решения уравнения путём последовательных приближений (итераций). Самый простой из них – метод половинного деления. Если мы определим числовой отрезок аргумента x, на котором существует корень, и функция на краях этого отрезка принимает значения разных знаков, то можно использовать метод половинного деления [2]. Можно использовать и другие методы, например дополнительные возможности приложения MS Excel 2010: встроенный язык программирования Visual Basic for Applications (VBA) и надстройку Поиск решения.

Приближенное решение нелинейных уравнений

Содержательная постановка задачи

Задача: Найти корень уравнения x3 – cosx = 0 приближёнными методами (графическим и численным методом деления пополам числового отрезка аргумента) на языках программирования Python и Visual Basic for Applications (VBA), а также надстройки Поиск решения в приложении MS Excel 2010.

Формальная модель

Формальная модель задана уравнением x3 – cosx = 0.

Приближенное решение уравнений с заданной точностью на языке Python

Компьютерная модель

Для нахождения корня уравнения разработаем компьютерную модель (скрипты) на языке программирования Python с использование графического и численного методов решения (рис. 1, рис. 2).

Графический метод

В начало программного кода ввести модули для работы с графикой matplotlip и функцией cos(x), установим пределы по оси x и y.

Программный код (скрипт):

#Графическое решение уравнения

import numpy as np #импортировать модули для работы с графикой

import matplotlib.pyplot as plt

#импортировать модуль для работы с функцией cos(x)

from math import cos

#построить график уравнения

plt.figure() #создать график

plt.xlim(-2, 2) #установить пределы графика по оси x

plt.ylim(-2, 2) #установить пределы графика по оси y

plt.title("Графическое решение уравнения") #установить имя графика

plt.xlabel("Ось x") #установить название оси x

plt.ylabel("Ось y") #установить название оси y

plt.grid() #добавить сетку на график

#Функция linspace() создает последовательность данных,

#равномерно расположенных на числовой прямой в заданном интервале

x = np.linspace(-2,2,100)

y1 = np.cos(x) #найти значение cos(x)

y = x**3 - y1 #найти значение уравнения

plt.plot(x,y,"b-") #построение графика сплошной линией синего цвета

plt.show() #показать график на экране

Запустить скрипт на выполнение, выполнив команду [Run – Run Module (F5)].

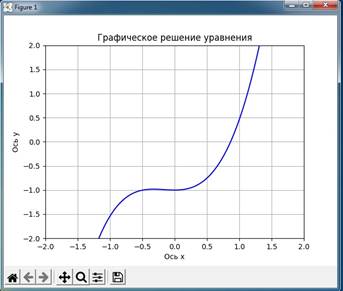
Рис. 1. Графическое решение уравнения на языке Python

График функции пересекает ось X один раз, следовательно, уравнение имеет один корень. По графику грубо приближённо можно определить, что x » 0,8 [1].

Численный метод половинного деления

Идея метода состоит в выборе точности решения и сведении первоначального числового отрезка [A; B], на котором существует корень уравнения, к отрезку заданной точности. Процесс заключается в последовательном делении отрезков пополам точкой C = (A + B) / 2 и отбрасыванию той половины отрезка [А; C] или [C; B], на котором корня нет.

Выбор нужной половины отрезка основывается на проверке знаков значений функции на его краях. Выбирается та половина, на которой произведение значений функции на краях отрицательно, т. е. когда функция имеет разные знаки – пересекает ось абсцисс.

Процесс продолжается до тех пор, пока длина числового отрезка не станет меньше заданной удвоенной точности. Деление этого отрезка пополам даёт значение корня с заданной точностью x » (A + B) / 2.

1. Поместить на форму (рис. 2):

· текстовые поля для ввода A и B;

· текстовое поле для ввода точности вычислений P;

· текстовое поле для вывода значений корня;

· четыре надписи для вывода обозначений;

· кнопку Button для запуска скрипта.

2. Ввести программный код, позволяющий вычислить корень уравнения методом половинного деления с использованием цикла с постусловием, который будет выполняться, пока выполняется условие (B - A) / 2 > P.

3. В начало программного кода ввести модуль для работы с графикой Tkinter и функцией cos.

Программный код (скрипт):

#Численное решение уравнения

#Подключить графическую библиотеку Tkinter

from tkinter import *

import tkinter

top=tkinter.Tk()

#Подключить модуль math

from math import cos

#Функция пользователя для командной кнопки

def process():

L2=Entry.get(E1)

L3=Entry.get(E2)

L4=Entry.get(E3)

#Ввод данных с преобразованием типа (float)

L2=float(L2)

L3=float(L3)

L4=float(L4)

while True:

L5 = (L2 + L3) / 2

if (L2*L2*L2 - cos(L2)) * (L5*L5*L5 - cos(L5)) < 0:

L3 = L5

else:

L2 = L5

if (L3 - L2) / 2 < L4: break

Entry.insert(E4,0,L5)

print(L5)

#Чтобы добавить текст, создать 4 компонента (виджет Label),

# ввести названия и установить их позиции

L1=Label(top,text="Численный метод",).grid(row=0,column=1)

L2=Label(top,text="A =",).grid(row=1,column=0)

L3=Label(top,text="B =",).grid(row=2,column=0)

L4=Label(top,text="P =",).grid(row=3,column=0)

L5=Label(top,text="X =",).grid(row=4,column=0)

#Для ввода информации создать 4 компонента (текстовые поля - Entry)

E1=Entry(top,bd =5)

E1.grid(row=1,column=1)

E2=Entry(top,bd =5)

E2.grid(row=2,column=1)

E3=Entry(top,bd =5)

E3.grid(row=3,column=1)

E4=Entry(top,bd =5)

E4.grid(row=4,column=1)

#Создать командную кнопку (виджет – Button)

B=Button(top,text="Выполнить",command = process).grid(row=5,column=1)

top.mainloop()

4. Запустить скрипт на выполнение, выполнив команду [Run – Run Module (F5)].

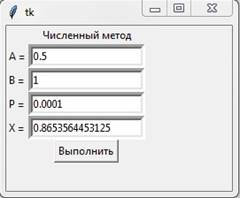
Рис. 2. Приближённое решение уравнения на языке Python

с заданной точностью

Из графика функции (рис. 1) видно, что корень находится на отрезке [0.5; 1]. Введём в текстовые поля значения концов числового отрезка, а также точность вычислений (например, 0.0001). На надпись будет выведено значение корня: x » 0. 8653564453125 [3].

Приближенное решение уравнений с заданной точностью в приложении MS Excel 2010

Компьютерная модель

Для нахождения корня уравнения разработаем компьютерную модель в приложении MS Excel. Представим функцию в табличной форме (рис. 3), построим её график (рис. 4), который позволит определить корень уравнения грубо приближённо.

Графический метод

Представить заданное уравнение в табличной форме.

1. В ячейку A1 ввести x.

2. В ячейку A2 ввести: y = x3 – cosx; поставить курсор после x; для степени выполнить команду [Вставка – Символ – Юникод (шестн.) – Найти в таблице нужное число], кликнуть по найденному числу или нажать на кнопку Вставить.

3. Выделить диапазон ячеек B1:I1 и B2:I2, щёлкнуть правой кнопкой; выполнить команду [Формат ячеек – Числовой – Число десятичных знаков – 3] <OK>.

4. В ячейку B1 ввести значение 0,000.

5. В ячейку C1 ввести формулу: =B1+0,200.

6. Выделить ячейку C1, щёлкнуть правой кнопкой, в меню выбрать [Копировать], выделить диапазон ячеек D2:I2, по выделенным ячейкам щёлкнуть правой кнопкой и выбрать команду [Вставить].

7. В ячейку B2 ввести формулу: =B1^3-COS(B1).

8. Выделить ячейку B2. Выполнить команды пункта 6.

9. Для изменения границ выделенных ячеек выполнить команду [Главная – Границы – Все границы].

Рис. 3. Табличное представление уравнения

10. Выделить в таблице данные по Y (ячейки диапазона A2:I2) и построить График с маркерами, выполнив команду [Вставка – Диаграммы – График] [2].

11. Под маркерами ввести подписи данных: выделить построенный график и выполнить команду [Макет – Подписи данных – Справа].

12. Для нанесения сетки выполнить команду [Главная – Макет – Сетка – Вертикальные линии – Основные линии сетки].

13. Чтобы перенести подписи единичных отрезков по оси X вниз, необходимо Выделить график и выполнить команду [Макет – Оси – Основная горизонтальная – Дополнительные параметры основной горизонтальной оси… – Подписи оси – Внизу].

14. Для корректировки единичных отрезков по оси X согласно исходным данным выполнить команды:

· щелкните правой кнопкой мыши по оси X графика, значения которого вы хотите изменить;

· в появившемся меню нажмите Выбрать данные и далее на Изменить;

· в таблице выделить ячейки по строке X, содержащие диапазон значений, на которые необходимо заменить текущие и нажать на кнопку <OK>.

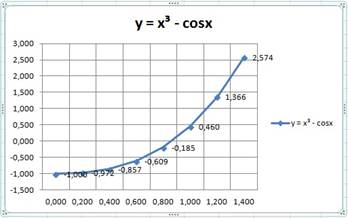
Рис. 4. График функции

По графику приближённо можно определить, что x » 0,800.

Численный метод половинного деления на языке VBA

1. Для создания графического интерфейса в MS Excel 2010 запустить систему объектно-ориентированного программирования Visual Basic for Applications (VBA) командой [Файл – Параметры – Настройка Ленты – Основные вкладки – Разработчик] <OK>. Для входа в систему выполнить команду [Разработчик – Visual Basic] или с помощью функциональных клавиш (Alt + F11 – войти в VBA; Alt + Q – закрыть VBA).

2. В окно интерфейса системы добавить форму командой [Insert – UserForm].

3. Поместить на форму (рис. 5):

· кнопку CommandButton1 для запуска событийной процедуры;

· два текстовых поля TextBox1 и TextBox2 для ввода числовых значений концов отрезка A и B;

· текстовое поле TextBox3 для ввода точности вычислений P

· надпись Label5 для вывода значений корня;

· четыре надписи для вывода обозначений (Label1 – Label4).

Рис. 5. Графический интерфейс проекта

4. Ввести программный код, позволяющий вычислить корень уравнения методом половинного деления с использованием цикла с постусловием, который будет выполняться, пока выполняется условие (B - A) / 2 > P.

Программный код:

‘Численное решение уравнения

‘Объявить исходные данные типа Single

Dim A, B, C, P As Single

Private Sub CommandButton1_Click()

‘В текстовые окна ввести значения переменных

A = Val(TextBox1.Text)

B = Val(TextBox2.Text)

P = Val(TextBox3.Text)

‘Цикл с постусловием

Do

C = (A + B) / 2

If (A ^ 3 - Cos(A)) * (C ^ 3 - Cos(C)) < 0 Then

B = C

Else

A = C

End If

Loop While (B - A) / 2 > P

‘Полученный результат занести в Label5

Label5 = (A + B) / 2

End Sub

5. Запустить программу, выполнив команду [Run – Run Sub/UserForm F5].

На надпись Label5 будет выведено значение корня: x » 0,86541748046875 (рис. 6).

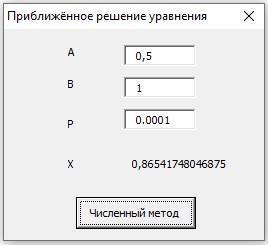
Рис. 6. Выполнение программного кода

Для сохранения программного кода выполнить команду [кнопка Файл – Сохранить как… - Выбрать папку для сохранения документа – Имя файла (Книга1) – Тип файла (Книга Excel с поддержкой макросов) - Сохранить].

Для повторного запуска программного кода выполнить команды:

1. Войти в приложение MS Excel 2010.

2. Выполнить команду [кнопка Файл – Параметры – Центр управления безопасностью – Параметры центра управления безопасностью – Параметры макросов – Включить все макросы (не рекомендуется)] <ОК>.

3. Выполнить команду [кнопка Файл – Открыть – Книга1 – Открыть].

4. Войти в среду программирования Visual Basic: [Разработчик – Visual Basic].

5. По окончании работы выполнить команду [Отключить все макросы без уведомления].

Надстройка – Поиск решения

Установим надстройку Поиск решения, войдя в приложение MS Excel 2010.

1. В появившемся диалоговом окне ввести команду [Файл – Параметры – Надстройки]. В окне Параметры Excel щёлкнуть по кнопке Перейти и поставить галочку Поиск решения, нажать < OK >.

2. В табличном процессоре Microsoft Excel 2010 ввести команду [Данные – Поиск решения].

3. В диалоговом окне Поиск решения установить:

· установить целевую ячейку, т.е. адрес целевой ячейки, предварительно выделив ячейку $F$2;

· вариант оптимизации значения целевой ячейки (максимизация, минимизация или Значения – 0);

· адрес ячейки, значения которой изменяются в процессе поиска решения (в которых хранятся значения параметров – $F$1).

4. Нажать на кнопку Найти решение.

5. В ячейке аргумента F1 появится подобранное значение 0,865. Таким образом, корень уравнения x » 0,865473833 найден с заданной точностью (рис. 7).

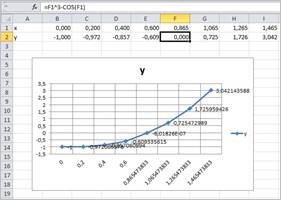
Рис. 7. Табличное и графическое представление уравнения

с заданной точностью (Надстройка – Поиск решения)

Анализ полученных результатов

Таблица № 1. Полученные результаты вычислений

Анализируя полученные данные (табл. 1), можно сделать вывод: численные методы решения уравнения (итерации) с заданной точностью дают более точные результаты по сравнению с графическими методами решения задачи (0,800 ® 0,865); из трёх рассмотренных численных методов решения – наиболее точный результат получен при использовании надстройки Поиск решения в приложении MS Excel 2010: x » 0,865473833.

Заключение

Поскольку рассмотренный в данной работе пример решения заданного нелинейного уравнения нельзя решить путём равносильных алгебраических преобразований, рассмотрены пять вариантов решения приближённо с заданной точностью (0,001 - 0.0001), используя языки объектно-ориентированного программирования Python, Visual Basic for Applications и табличный процессор MS Excel 2010 графическими и итерационными методами.

Для решения уравнения на языках программирования точность вычисления корня зависит не только от параметров используемого численного метода, но и от типа переменной.

Для решения уравнения в приложении MS Excel точность подбора зависит от заданной точности представления числа в ячейках таблицы.

Проведённый компьютерный эксперимент наглядно показывает практическую значимость проведённых исследований.

Таким образом, исследование компьютерной модели показало, что решение с заданной точностью даёт более точные результаты по сравнению с графическим методом решения задачи (0,800 ® 0,865).

При использовании языков программирования Python и Visual Basic for Applications (VBA) для приложения MS Excel 2010, а также надстройки Поиск решения были получены следующие значения: x » 0.8653564453125, x » 0.86541748046875, x » 0,865473833; последний вариант (надстройка - Поиск решения) – наиболее точный.

Программное обеспечение

1. Операционная система Windows 10

2. Среда программирования Python – 3.8.0

3. Приложение Microsoft Office Excel 2010

4. Приложение Microsoft Office Word 2010