Данная статья является сокращением основной работы. С дополнительными приложениями и фотографиями можно ознакомиться на сайте II Международного конкурса научно-исследовательских и творческих работ учащихся «Старт в науке» по ссылке: https://www.school-science.ru/2017/7/26525
Цель работы – изучить способы решения неравенств с двумя переменными, содержащих знак модуля.
Поставленная цель обусловила решение ряда задач:
1) изучить теоретический материал о неравенствах и модуле числа, на котором будет основываться исследование;
2) проанализировать практическое применение данного материала посредством решения типовых заданий;
3) рассмотреть различные способы решения неравенств с двумя переменными, содержащих знак модуля;
4) провести анализ сходств и различий данных способов;
5) систематизировать материал и вывести алгоритм решения данных неравенств различными способами;
6) рассмотреть практическое применение данных способов при решении неравенств с двумя переменными, содержащих знак модуля.
Актуальность данной темы обусловлена тем, что задания на неравенства с двумя переменными, содержащими знак модуля, встречаются в заданиях С части ЕГЭ, но не изучаются глубоко в школьном курсе математики (без углубленного изучения).
Объектом исследования являются неравенства с двумя переменными, содержащих знак модуля.
Предметом исследования являются способы решения данных неравенств.
Гипотеза: не все способы решения являются универсальными, поэтому в зависимости от общего вида неравенства и места расположения модуля будем выбирать тот или иной способ решения данных неравенств.
Типовые тестовые задания, содержащие переменную под знаком модуля
Задание № 1. Найти площадь фигуры, заданной неравенством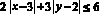 
.
Решение: Множество точек – ромб, полученный из ромба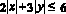 
путем параллельного переноса точки пересечения диагоналей (0;0) в точку (3;2).
Диагонали ромба: d1 = 6, d2 = 4S = 0,5d1d2 = 0,5 * 4 * 6 = 12.
Ответ: S = 12
Задание № 2. Изобразите на координатной плоскости фигуру, заданную неравенством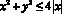 
и вычислить ее площадь.
Решение: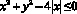 
;
;
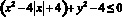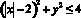
Это два симметричных относительно оси OY круга с центрами в точках (–2;0) и (2;0) и радиусом r =2.
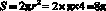
Ответ: 
.
Задание № 3. Изобразите фигуру, заданную неравенством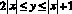 
и найдите площадь данной фигуры.
Решение: данная фигура состоит из двух равных треугольников OCB и OAB, вершины которых имеют координаты:
A = (1;2), B = (0;1), C = (–1;2).
Рассмотрим треугольник OAB: основание OB равно 1; высота, опущенная из вершины А к основанию равно 1.
SOAB = 0,5·h·OB = 0,5·1·1 = 0,5 Так как треугольника равные, то S = 2SOAB = 1.
Ответ: S = 1.
Задание № 4. Найдите S фигуры, заданной неравенством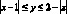 
.
Решение: фигура, заданная неравенством – прямоугольник ABCD с вершинами
, 
, 
, 
.
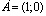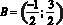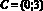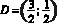Для нахождения площади необходимы значения сторон AB и AD:
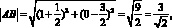
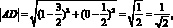
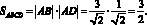
Ответ: S = 1,5.
Задание № 5.
Изобразите фигуру, заданную системой неравенств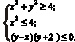 
. Найдите площадь данной фигуры.
Решение. Первое неравенство системы задает круг с радиусом 2 и центром в начале координат. Второе неравенство задает прямые x = –2 и x = 2, множество точек располагается между этими прямыми. Третьим неравенством задаются прямые y = –2 и y = x, множество точек располагается выше прямой y = –2 и ниже прямой y = x
Фигура является общей частью внутренности прямоугольного треугольника ABC и внешности круга радиусом 2 с центром в начале координат.
Вершины треугольник АBC имеют координаты:
А(–2;–2), В(2;2), С(2;–2)
Найдем площадь прямоугольного треугольника:
.
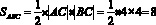Для того, чтобы вычислить площадь фигуры нужно из площади треугольника ABC вычесть площадь полукруга с радиусом 2:
.
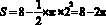Ответ: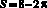 
.
Задание № 6. Найдите площадь фигуры, заданной неравенством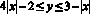 
.
Решение: Фигура состоит их двух равных треугольников OCB и OAB, вершины которых имеют координаты A = (1;2), B = (0;3), C = (–1;2)
Основание треугольника OAB равно 3, а высота, опущенная к основанию из вершины А равна 1.
SOAB = 0,5·h·OB = 0,5·3·1 = 1,5
Треугольники равны, поэтому S = 2SOAB = 3.
Ответ: S = 3.
Задание № 7. Решите систему неравенств:
.
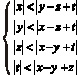Решение.
Предположим, что данная система неравенств имеет решение x, y, z, t.
Тогда, в частности,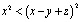 
, т.е. 
.
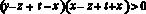Аналогично получаем:
;
;
.
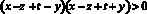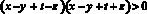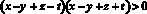Перемножим все полученные неравенства: с одной стороны, произведение четырех положительных чисел положительно, с другой стороны, это произведение равно:
.
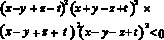Приходим к противоречию.
Ответ: система не имеет решений.
Задание № 8. Существуют ли действительные числа a, b и с такие, что при всех действительных x и y выполняется неравенство:
.
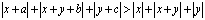Решение: предположим, такие числа a, b, с существуют. Выберем x > 0 и y > 0 такие, что
;
;
.
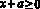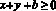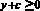Тогда разность между левой и правой частями равна a + b + с.
Если взять x < 0 и y < 0 такие, что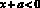 
;
;
,
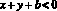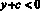тогда разность будет равна –a – b – с.
Таким образом, с одной стороны a + + b + с > 0, с другой стороны a + b + с < 0, что является противоречием.
Ответ: нет, такие числа не существуют.
Задание № 9. Сколько различных целочисленных решений имеет неравенство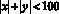 
?
При натуральных n уравнение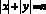 
имеет ровно 4n целочисленных решений, а при n = 0 решение единственно. Таким образом, количество решений исходного неравенства равно: 1 + 4(1 + + 2 + 3 + … + 99) = 19 801.
Ответ: 19 801.
Способы решение неравенств с двумя переменными, содержащих знак модуля
Рассмотрим решение неравенств с двумя переменными, содержащие знак модуля, тремя способами:
1. Использование свойств неравенств, путем равносильных преобразований, и правил решения дробных неравенств.
2. Умножение обеих частей неравенства на неотрицательное число и дальнейшее решение полученного неравенства.
3. Возведение обеих частей в квадрат и решение полученного дробно-рационального неравенства.
Для того, чтобы рассмотреть все три способа, берем одно и тоже неравенство:
.
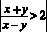Способ № 1. Использование свойств неравенств, путем равносильных преобразований.
Равносильные переходы при решении неравенств.
Если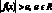 
, то при а > 0 – множество решений совпадает с областью определения функции f(x), а при 
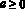равносильно
,
.
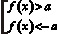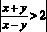При решении воспользуемся теоремой:
.
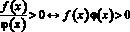Таким образом данное неравенство равносильно совокупности неравенств:
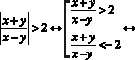
Перенесем 2 и –2 в левую часть и приведем к общему знаменателю. (1)
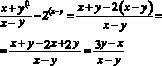
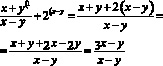(1)
Имеем:
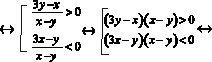
Воспользуемся тем, что
- произведение двух множителей < 0, если каждый множитель > 0 (или каждый < 0);
- произведение двух множителей < 0, если один из множителей < 0, а другой > 0,
и запишем данную совокупность в виде совокупности систем, применив данное чередование к каждому из неравенств. Решим данные совокупности систем неравенств:
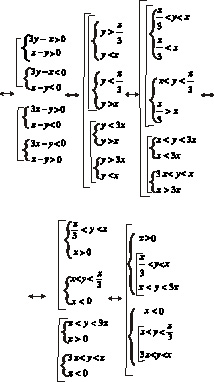
Геометрическим решением данного неравенства являются все точки, лежащие в углах АОВ и А1ОВ1, исключая точки, расположенные на лучах ОА, ОD, ОВ и ОА1, ОС, ОВ1.
Способ №1 является наиболее универсальным при решении неравенств. Если неравенство удовлетворяет одному из равносильных переходов, то оно может быть решено данным способом.
Способ № 2. Умножение обеих частей на неотрицательное число
Так как модуль частного равен частному модулей, то:
.
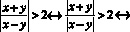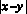есть число неотрицательное и от умножения на него данного неравенства равносильность не нарушается, если 
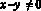, поэтому:
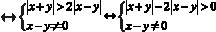
Далее для решения будем использовать метод равносильных преобразований.
Воспользуемся методом одновременного раскрытия модуля и его определением:
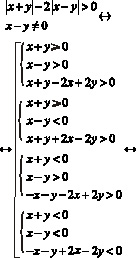
Решим данные неравенства:
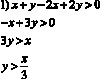
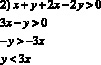
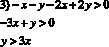
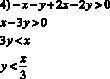
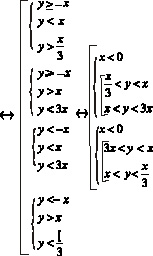
Геометрическим решением данного неравенства являются все точки, лежащие в углах АОВ и А1ОВ1, исключая точки, расположенные на лучах ОА, ОD, ОВ и ОА1, ОС, ОВ1.
Данный способ наиболее удобен при решении дробно-рациональных неравенств.
Способ №3. Возведение обеих частей в квадрат.
Так как модуль частного равен частному модулей, то:
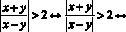
Так как обе части неравенства – числа неотрицательные, то равносильность не нарушается при возведении в квадрат обеих частей неравенства.
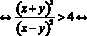
Перенесем 4 в левую сторону и приведем к общему знаменателю.
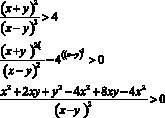
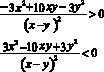
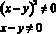
Таким образом данное неравенство равносильно системе:
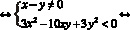
Неравенство разложим на множители способом группировки.
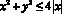
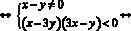
Переходим к совокупности систем и решаем с учетом чередования знаков, как при способе равносильных преобразований.
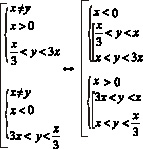
Геометрическим решением данного неравенства являются все точки, лежащие в углах АОВ и А1ОВ1, исключая точки, расположенные на лучах ОА, ОD, ОВ и ОА1, ОС, ОВ1.
Данный способ можно использовать, если обе части неравенства есть числа неотрицательные, а возведение в квадрат не ведет к усложнению решения.
Вывод
Научная новизна исследования:
– рассмотрено три способа решения одного неравенства с двумя переменными, содержащими знак модуля;
– выведен алгоритм для каждого из трех способов решения неравенств;
– даны рекомендации по выбору способа решения;
– представлено приложение с решением неравенств различными способами.
Нужно заметить, что каждый из способов имеет свои преимущества, поэтому для успешного решения данных неравенств необходимо знать все способы. А какой из них наиболее удобный, зависит от вашего решения.
Практическая значимость исследования:
– может быть использовано учителями математики при подготовке к урокам, при изучении тем: «Координаты и графики» и «Решение неравенств», и факультативным занятиям.
– может быть использовано при проведении факультативных занятий и элективных курсов.
– для самостоятельной подготовки учащимися к ЕГЭ и вступительным экзаменам.
Рис. 1. Алгоритм решения неравенств с двумя переменными, содержащих знак модуля
Библиографическая ссылка
Дерябина А.А. НЕРАВЕНСТВА С ДВУМЯ ПЕРЕМЕННЫМИ, СОДЕРЖАЩИЕ ЗНАК МОДУЛЯ // Международный школьный научный вестник. – 2017. – № 2. ;URL: https://school-herald.ru/ru/article/view?id=179 (дата обращения: 24.04.2024).