На уроках математики изучаются различные способы решения иррациональных, дробно–рациональных, целых и других уравнений. К примеру, иррациональные уравнения решались методами возведения обеих частей в одну и ту же натуральную степень; введением вспомогательных переменных; умножения обеих частей уравнения на сопряженное выражение и т.д.
В математическом анализе изучаются свойства функций, а затем они применяются при решении уравнений или неравенств, как например, монотонность. Заметим, что функции–радикал, степенная функция, логарифмическая – выпуклые функции. Причем все из них – строго выпуклые вверх/вниз. Появилась гипотеза: можно ли и это свойство применять при решении задач алгебры. Предмет исследования: приемы решения уравнений, основанные на свойствах выпуклой функции.
Цель исследования: изучить метод, основанный на свойствах выпуклых функций, позволяющий решать уравнения.
Задачи исследования:
– изучить свойства строго выпуклых функций, геометрический смысл выпуклости;
– найти применения свойств выпуклых функций при решении уравнений;
– решить уравнения с применением свойств выпуклых функций;
– провести решения уравнения различными возможными способами и выявить наиболее рациональный из них.
В ходе ознакомления с методом решения уравнений с помощью свойств выпуклых функций, опубликованном в журналах «Математика в школе» в 2002 в № 2 [1] и 2005 и в № 5 [2], а также с исследовательской работой Макиевой Л.А. «Выпуклые функции и уравнения» (Электронный ресурс) [3], был сделан вывод, что некоторые уравнения довольно легко решаются указанным методом, но ему не ставился в сравнение другой метод. В данной работе некоторые уравнения решались двумя методами для определения наиболее рационального из них.
Теоретическая часть
Определение. Функция, непрерывная на некотором промежутке, называется выпуклой вниз, если для любых точек из промежутка выполняется неравенство
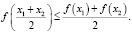
Определение. Функция, непрерывная на некотором промежутке, называется выпуклой вверх (вогнутой), если для любых точек из этого промежутка выполняется неравенство
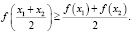
Определение. Пусть функция f(x) определена на промежутке Х. Эта функция называется строго выпуклой вниз (вверх) на Х, если для любых 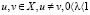 справедливо неравенство
справедливо неравенство
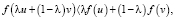
соответственно
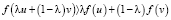 .
.
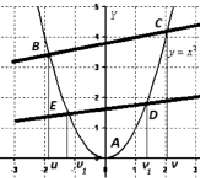
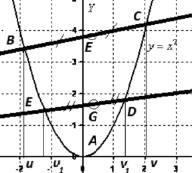
Геометрически это означает, что любая точка хорды BC, отличная от точек BC, лежит выше (ниже) точки A графика функции f(x), соответствующей тому же значению аргумента. Сегменты числовой прямой с концами в точках 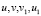 имеют общую середину.
имеют общую середину.
Теорема 1. Пусть функция f(x) является строго выпуклой вниз на промежутке Х, 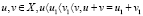 . Тогда справедливо неравенство
. Тогда справедливо неравенство 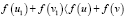 .
.
Доказательство. Так как 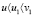 , то найдется величина λ, такая, что
, то найдется величина λ, такая, что 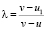 и
и 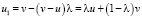 и
и 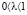 . Тогда
. Тогда
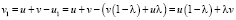
и, значит,
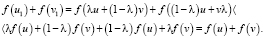
Ч. т.д.
Геометрический смысл теоремы очевиден: если выполнены условия теоремы, то середина отрезка BC – точка F лежит выше середины отрезка ED – точки 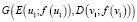 , так как ордината точки F равна половине
, так как ордината точки F равна половине 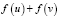 , ордината точки G – половине
, ордината точки G – половине 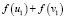 . Далее будем ссылаться на эти условия:
. Далее будем ссылаться на эти условия: 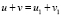 (1),
(1), 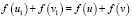 (2).
(2).
Теорема 2. Если функция f(x) является строго выпуклой на промежутке Х, функции 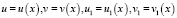 , такие, что при всех x из ОДЗ уравнения (1) их значения
, такие, что при всех x из ОДЗ уравнения (1) их значения 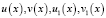 содержатся в промежутке Х и выполнено условие (2), то уравнение (1) на ОДЗ равносильно совокупности уравнений
содержатся в промежутке Х и выполнено условие (2), то уравнение (1) на ОДЗ равносильно совокупности уравнений 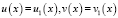 . (3)
. (3)
Доказательство. В самом деле, очевидно, что решения совокупности уравнений (3), содержащиеся в ОДЗ уравнения (1), будут решениями уравнения (1).
Предположим, что x0 – решение уравнения (1), не являющееся решением совокупности уравнений (3). Тогда
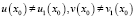 .
.
Для определенности предположим, что функция f(x) является строго выпуклой вниз на промежутке Х и 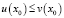 . Тогда справедлива одна из цепочек неравенств:
. Тогда справедлива одна из цепочек неравенств:
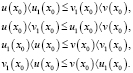
Отсюда в силу теоремы 1 получаем, что либо
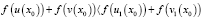 ,
,
либо
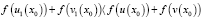 ,
,
что противоречит предположению. Следовательно, решения уравнения (1) являются решениями совокупности уравнений (3). Ч. т. д.
Вместо совокупности уравнений (3) в условиях теоремы 2 можно брать равносильные совокупности, например,
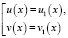 или
или 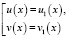
Конструировать уравнения можно, опираясь только на определение строго выпуклой функции. Для выделения этого класса сформулируем и докажем утверждение.
Теорема 3. Если функция f(x) является строго выпуклой на промежутке Х и 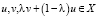 . Тогда равенство
. Тогда равенство 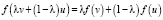 (8) справедливо в том и только в том случае, если либо u = v, либо λ = 0, либо λ = 1.
(8) справедливо в том и только в том случае, если либо u = v, либо λ = 0, либо λ = 1.
Доказательство. Очевидно, что если либо u = v, либо λ = 0, либо λ = 1, то равенство (8) верно.
Пусть, для определенности, функция f(x) является строго выпуклой вниз на промежутке Х и 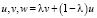 принадлежит промежутку Х. Допустим, что
принадлежит промежутку Х. Допустим, что 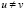 . Если
. Если 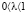 , то равенство (8) невозможно по определению.
, то равенство (8) невозможно по определению.
Предположим, что 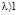 и
и 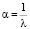 . Тогда
. Тогда 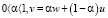 и
и
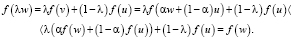
Поэтому λ не может быть меньше 0. Следовательно, либо u = v либо λ = 0 либо λ = 1 Ч. т. д.
Геометрический смысл теоремы 3: если функция f(x) является строго выпуклой на числовой прямой и u ≠ v, то прямая, проходящая через точки 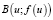 и
и 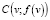 , пересекает график функции только в этих точках [1].
, пересекает график функции только в этих точках [1].
Примеры применения выпуклых функций
§ 1. Решение иррациональных уравнений
Пример 1. Решить уравнение
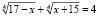 .
.
Решение.
Находим ОДЗ уравнения: 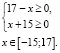
Пусть 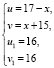 так как
так как 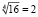 , значит правая часть уравнения это
, значит правая часть уравнения это 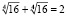 .
.
Проверим выполнение условия теоремы 2:
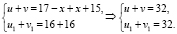
Верно, значит, уравнение на ОДЗ равносильно равносильным совокупностям уравнений:
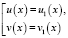 или
или 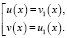
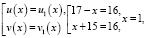
что удовлетворяет ОДЗ.
Ответ: x = 1.
Пример 2. Решить уравнение
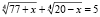 .
.
Решение.
Находим ОДЗ уравнения:
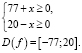
Пусть 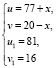 так как
так как 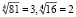 , значит правая часть уравнения это
, значит правая часть уравнения это 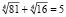 .
.
Проверим выполнение условия теоремы 2:
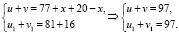
Верно, значит, уравнение на ОДЗ равносильно равносильным совокупностям уравнений:
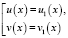 или
или 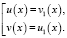
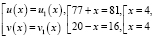
или
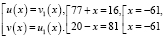
что удовлетворяет ОДЗ.
Ответ: x = 4, x = – 61.
Пример 3. Решить уравнение
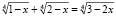 .
.
Решение.
Находим ОДЗ уравнения: 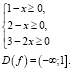
Пусть 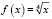 ,
, 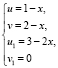 .
.
Проверим выполнение условия теоремы 2:
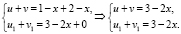
Верно, значит, уравнение на ОДЗ равносильно равносильным совокупностям уравнений:
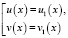 или
или 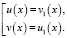
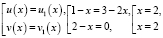
полученное решение не удовлетворяет ОДЗ. Решим вторую совокупность уравнений:
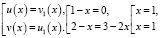
что удовлетворяет ОДЗ.
Ответ: x = 1.
Пример 4. Решить уравнение
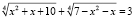 .
.
Решение.
Находим ОДЗ уравнения:
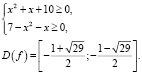
Пусть 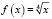 ,
, 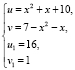 , так как
, так как 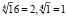 , значит правая часть уравнения это
, значит правая часть уравнения это 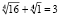 .
.
Проверим выполнение условия теоремы 2:
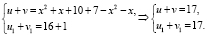
Верно, значит, уравнение на ОДЗ равносильно равносильным совокупностям уравнений:
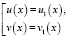 или
или 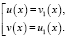
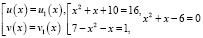
решим уравнение по теореме Виета:
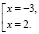
Полученные решения удовлетворяют ОДЗ. Решим вторую совокупность уравнений:
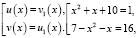
полученные уравнения решений не имеют.
Ответ: x = – 3, x = 2.
Пример 5. Решить уравнение
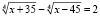 .
.
Решение.
Находим ОДЗ уравнения:
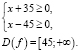
Пусть 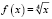 ,
, 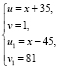 , так как
, так как 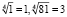 , значит правая часть уравнения это
, значит правая часть уравнения это 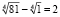 .
.
Проверим выполнение условия теоремы 2:
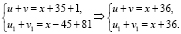
Верно, значит, уравнение на ОДЗ равносильно равносильным совокупностям уравнений:
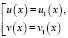 или
или 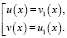
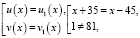
решений нет. Решим вторую совокупность уравнений:
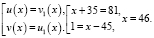
Полученное решение входит в ОДЗ.
Ответ: x = 46.
§ 2. Примеры уравнений, в решении которых участвуют функции, отличные от 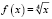 .
.
Пример 6. Решить уравнение
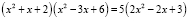 .
.
Решение.
Прологарифмировав обе части уравнения, получаем равносильное уравнение
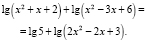
Пусть 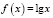 ,
, 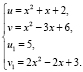
Так как функция 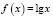 является строго выпуклой вверх на
является строго выпуклой вверх на 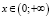 , функции
, функции 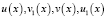 положительны при любом x и выполнено условие теоремы 2:
положительны при любом x и выполнено условие теоремы 2:
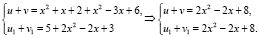
Исходное уравнение равносильно совокупности уравнений:
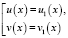 или
или 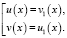
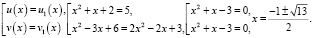
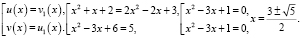
Полученные решения входят в ОДЗ.
Ответ: 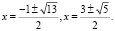
Пример 7. Решить уравнение 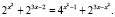
Решение.
Пусть 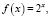
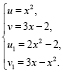
Так как функция f(x) является строго выпуклой вниз на R и выполнено условие 2 теоремы 2:
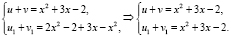
Исходное уравнение равносильно совокупности уравнений:
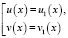 или
или 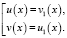
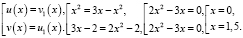
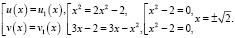
Полученные решения входят в ОДЗ.
Ответ: 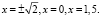
Пример 8. Решить уравнение 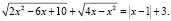
Решение.
Преобразуем уравнение в виде
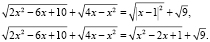
Пусть 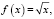
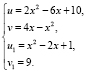
Так как функция f(x) является строго выпуклой вверх на 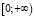 и выполнено условие 2 теоремы 2:
и выполнено условие 2 теоремы 2:
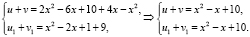
Исходное уравнение равносильно совокупности уравнений:
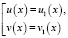 или
или 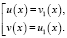
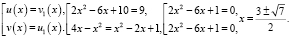
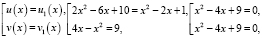
уравнение не имеет решений.
Полученные решения входят в ОДЗ.
Ответ: 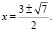
§ 3. Примеры уравнений, решение которых опирается на теорему 3.
Пример 9. Решить уравнение 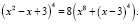
Решение.
Если предположить, что
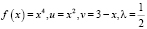 ,
,
т.к.
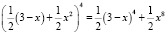 ,
,
тогда уравнение может быть записано в виде (8). Поскольку функция 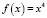 является строго выпуклой вверх на R, то по теореме 3 исходное уравнение равносильно уравнению
является строго выпуклой вверх на R, то по теореме 3 исходное уравнение равносильно уравнению 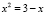 и, значит,
и, значит, 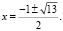
Ответ: 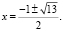
Пример 10. Решить уравнение
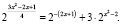
Решение.
Если предположить, что
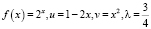 ,
,
т.к.
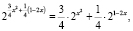
тогда уравнение может быть записано в виде (8). Поскольку функция 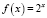 является строго выпуклой вниз на R, то по теореме 3 исходное уравнение равносильно уравнению
является строго выпуклой вниз на R, то по теореме 3 исходное уравнение равносильно уравнению 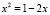 и, значит,
и, значит, 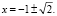
Ответ: 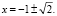
§ 4. Пример уравнения, опирающегося на теорему 1.
Пример 11. Решить уравнение 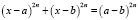 , где a ≠ b и
, где a ≠ b и 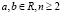 .
.
Решение.
Положив
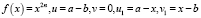 ,
,
замечаем, что уравнение относится к виду (1). Поскольку функция 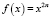 является строго выпуклой вниз на R и при всех x выполнено условие (2), то уравнение равносильно совокупности уравнений
является строго выпуклой вниз на R и при всех x выполнено условие (2), то уравнение равносильно совокупности уравнений 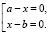 Cледовательно, оно имеет два решения
Cледовательно, оно имеет два решения 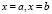 .
.
Ответ: 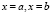 .
.
Сравнение способов решения некоторых уравнений
Пример 1. Решить уравнение
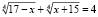 .
.
Решение.
Находим ОДЗ уравнения:
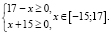
Возводим двукратно обе части уравнения в квадрат:
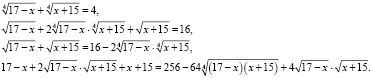
Тогда
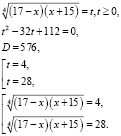
Первое уравнение: 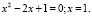 Второе уравнение корней не имеет.
Второе уравнение корней не имеет.
Ответ: x = 1.
Пример 5. Решить уравнение
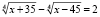 .
.
Решение.
Находим ОДЗ уравнения:
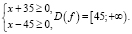
Представим левую часть уравнения в виде разности степеней и, так как показатель степеней удовлетворяет условиям: 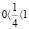 , воспользуемся неравенством Бернулли:
, воспользуемся неравенством Бернулли:
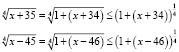
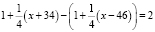
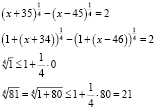
Получаем уравнение, записанное в виде:
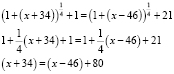
А это возможно, если 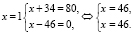
Ответ: x = 46.
Данное решение подразумевает такой подбор значений линейных двучленов, чтобы решалась система двух линейных уравнений.
Пример 6. Решить уравнение 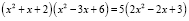 .
.
Решение.
Преобразуем данное уравнение: 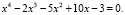
Решим его методом неопределенных коэффициентов:
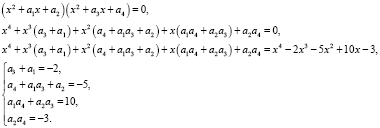
Положим, что 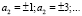 Если
Если 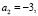 то
то 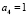 .
.
Тогда 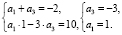
Итак, 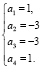
Значит, 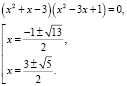
Ответ: 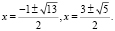
Как видно, знание свойств выпуклых функций упрощают решение уравнений, можно избежать громоздких вычисление и сложных преобразований уравнения. Заметим, что при решении первого уравнения вторым способом возможно допустить ошибки при расчете (двукратном возведении в квадрат, решении квадратных уравнений).
Заключение
В первом параграфе рассматривались уравнения вида 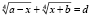 , где a, b, d – числа, a ≠ b. При решении иррациональных уравнений может возникнуть сложность, которую не всегда возможно преодолеть. Например, при решении предложенным способом уравнения
, где a, b, d – числа, a ≠ b. При решении иррациональных уравнений может возникнуть сложность, которую не всегда возможно преодолеть. Например, при решении предложенным способом уравнения 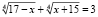 необходимо, чтобы
необходимо, чтобы 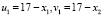 , где
, где 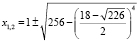 , о чем трудно догадаться. Сложность использованного метода при решении состоит также в «угадывании» представления числа d в виде
, о чем трудно догадаться. Сложность использованного метода при решении состоит также в «угадывании» представления числа d в виде 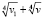 причем
причем 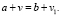
Решение традиционным способом уравнений занимает больше времени, предполагает большое количество вычислений (а, следовательно, и ошибок в них). К тому же, при двукратном возведении в квадрат получаем «лишние» корни, которые нужно обязательно проверять. При использовании неравенства Бернулли в решении иррационального уравнения создалась «трудность» на составление совместной системы двух линейных уравнений.
Способ с использованием свойств выпуклых функций позволяет решить «громоздкие» уравнения (а также трансцендентные). Но так как этот способ – эмпирический, его не всегда можно использовать.
Конструировать уравнения можно, опираясь только на определение строго выпуклой функции.
Таким образом, каждый из способов имеет свои плюсы и минусы, и только опыт научит правильно ими пользоваться.
Библиографическая ссылка
Липатова С.В. РЕШЕНИЯ УРАВНЕНИЙ, ОСНОВАННЫЕ НА СВОЙСТВАХ ВЫПУКЛОЙ ФУНКЦИИ // Международный школьный научный вестник. 2017. № 3-1. ;URL: https://school-herald.ru/ru/article/view?id=234 (дата обращения: 15.02.2026).
