В работе рассматривается взаимодействие многих частиц в системе путем компьютерного моделирования. Для системы частиц строится гистограмма их распределения по скоростям, и наблюдается зависимость вида этой гистограммы от количества рассчитанных шагов времени. Строятся графики зависимости коэффициента совпадения экспериментальной гистограммы с функцией Максвелла-Больцмана от количества пройденных шагов времени. Установлено, что чем больше частиц участвует в модели, тем больше коэффициент совпадения, и тем он больше, чем меньше шаг интегрирования.
Многие системы, такие как газы, жидкости и твердые тела, состоят из большого числа взаимодействующих друг с другом частиц.
Давайте рассмотрим чашку кофе. В чашке содержится примерно 1023 –1025 молекул, движение которых вместе с хорошей точностью подчиняется законам классической физики. Известно, например, что температура кофе, если его оставить в чашке, достигает комнатной и с течением времени больше не меняется. Как связана температура кофе с траекториями отдельных молекул? Почему она не зависит от времени, даже если траектории отдельных молекул непрерывно меняются?
Этот пример ставит нас перед проблемой: как можно, исходя из известных межмолекулярных взаимодействий, понять наблюдаемое поведение сложной многочастичной системы?
Одной из неизведанных, но очень важных для понимания природы областей человечества является микромир. Наших способностей пока недостаточно, чтобы заглянуть внутрь жизни молекул, но компьютеры уже позволяют нам увидеть эту жизнь в виде упрощенной модели. И цель нашей работы – изучение отличий в динамике поведения систем очень многих частиц (примерно 1023) и немногих частиц (порядка 103).
Самый очевидный подход для исследования большого числа взаимодействующих между собой частиц – это моделирование на компьютере. Однако известно, что для правильного исследования такой системы необходимо задать в модели столько частиц, чтобы их количество было много больше квадратного корня из их числа (как минимум 1 млн, где каждая частица будет взаимодействовать с каждой). Иначе расчёт не будет точным. Это колоссальный объем вычислений, и даже для такой, не очень точной системы понадобится суперкомпьютер и много времени. А мы же можем позволить себе лишь простой компьютер, поэтому придется порядками сократить количество частиц в модели. Тогда попробуем найти, на сколько система из немногих частиц будет отличаться от реальной. Поскольку мы хотим понять качественные свойства систем многих частиц, предположим, что молекулы будут химически инертными шариками. Посчитаем также, что сила взаимодействия любых двух молекул зависит только от расстояния между ними. В этом случае полная потенциальная энергия U определяется суммой двухчастичных взаимодействий:
U = V(r12) + V(r13) + … + V(r23) + … = =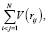 
(1)
где V(rij) зависит только от расстояния (rij) между частицами i и j. Такое парное взаимодействие характерно «простым» жидкостям, например жидкому аргону. Наиболее важными особенностями этого взаимодействия являются сильное отталкивание для малых r и слабое притяжение на больших расстояниях. Одной из наиболее употребительных формул для расчета V(r) является потенциал Леннарда-Джонса (рис. 1) [1]:
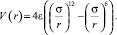(2)
Для численного интегрирования с целью расчета траектории каждой частицы был выбран метод Верле, так как алгоритмы Эйлера и Эйлера – Кромера не могут обеспечить должный порядок точности при моделировании молекулярной динамики.
Чтобы энергия системы сохранялась, необходимо убрать «жесткие» стенки и ввести периодические краевые условия (рис. 2) [1]. Для одномерного пространства это было бы эквивалентно сворачиванию отрезка, по которому движутся частицы, в кольцо, а для двумерного пространства – плоскость превратится в тор (рис. 3).
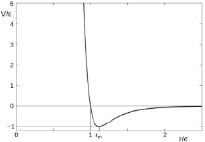
Рис. 1. График зависимости потенциала взаимодействия от расстояния
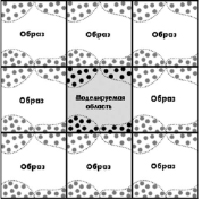
Рис. 2. Принцип введения периодических краевых условий
Далее нами была написана программа на языке c#. Программа рассчитывает и визуализирует поведение каждой точки в системе. Также она строит график распределения частиц по скоростям и, рядом с ним, график функции Максвелла-Больцмана – точный график, который получится при моделировании 1023 частиц (рис. 4).
Мы видим, что спустя некоторое время после начала работы, независимо от начальных данных, скорости частиц распределяются по кривой, похожей на кривую Максвелла-Больцмана. Но, все же, это не та кривая. По формуле
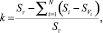
где Si >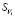 
;
Sг – Площадь под всей гистограммой,
Si – Площадь под столюцом гистограммы с номером i,
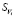– Площадь под столбцом функции Максвелла-Больцмана с номером i.
Рассчитываем коэффициент похожести в разные моменты времени и получаем разные графики. Графики 5-9 (рис. 5–9) построены для моделей из 100, 500 и 1000 частиц соответственно. Можно заметить, что чем больше частиц участвует в модели, тем больше и коэффициент похожести. Графики 6 и 7 и 8 и 9 отличаются величиной шага интегрирования, что говорит нам о том, что для большей точности нужно уменьшать шаг. Вид графика (его спад и »провалы») говорит нам о том, что в системе имеется постоянно накапливающаяся погрешность. Она возникает из-за слишком большого шага интегрирования. Уменьшение шага приведет к существенному увеличению времени расчетов. Для поиска оптимального шага в ближайшем будущем будет введен алгоритм Рунге-Кутты, оптимизированный для данной работы (поиск шага будет идти быстрее).
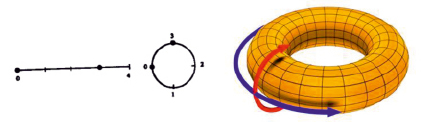
Рис. 3. Применение периодических краевых условий к одномерному и двумерному пространствам
Рис. 4. Скриншот работы программы, коэффициент 84 %
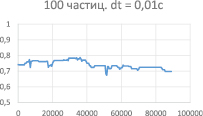
Рис. 5. «Коэффициент похожести» для 100 частиц
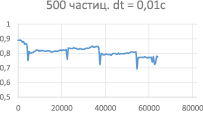
Рис. 6. «Коэффициент похожести» для 500 частиц
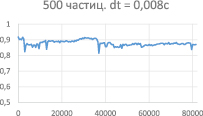
Рис. 7. «Коэффициент похожести» для 500 частиц (шаг интегрирования 0,008 с)
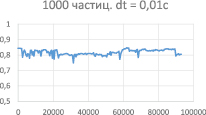
Рис. 8. «Коэффициент похожести» для 1000 частиц
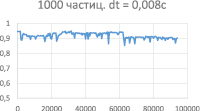
Рис. 9. «Коэффициент похожести» для 1000 частиц (шаг интегрирования 0,008 с)
В ближайшем будущем также планируется найти зависимость коэффициента похожести от характера газа, от времени, с минимизацией погрешности, и от разного другого количества частиц.
Библиографическая ссылка
Рухович И.В. ОТЛИЧИЯ В ДИНАМИКЕ ПОВЕДЕНИЯ СИСТЕМ МНОГИХ И ОЧЕНЬ МНОГИХ ЧАСТИЦ // Международный школьный научный вестник. – 2017. – № 3-1. ;URL: https://school-herald.ru/ru/article/view?id=247 (дата обращения: 27.04.2024).