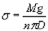В нем столько блеску было,
Была такая спесь!
А он - воды и мыла
Раздувшаяся смесь!
С. Маршак «Мыльные пузыри»
В настоящее время трудно точно сказать, когда люди впервые обратили своё внимание на поведение в природе мыльных пузырей. День рождения мыльного пузыря и по сей день остаётся загадкой. Но доподлинно известно, что при раскопках древней Помпеи археологи обнаружили необычные фрески с изображением юных помпейцев, выдувающих мыльные пузыри.
Так ли прост мыльный пузырь, как кажется с первого взгляда? Как исследовать объект, которого как бы и нет? На эти и другие вопросы мы ответим в нашей работе.
Цель: изучение мыльного пузыря как физического тела.
Задачи:
1. Проанализировать информацию по данному вопросу и исследовать физические и математические свойства мыльного пузыря.
2. Продемонстрировать невероятные свойства мыльного пузыря.
3. Подготовить материал для демонстрации на уроках физики, математики и во внеклассной работе.
Объект исследования: мыльный раствор
Предмет исследования: мыльный пузырь
Методы исследования: теоретические и практические (моделирование, экспериментальный)
Гипотеза: мыльный пузырь - основа для изучения многих природных явлений и законов.
Теоретическая часть
Что такое мыльный пузырь

Мыльный пузырь – это тонкая пленка мыльной воды, которая формирует шар с переливчатой поверхностью. Оболочка мыльного пузыря состоит из тонкого слоя воды, который заключен между двумя слоями молекул, обычно мыла или глицерина. В стакане вода имеет только одну свободную поверхность и соответственно, на ней может образовываться только один слой молекул мыла, а свободная пленка имеет две поверхности. Эти слои состоят из достаточно сложных молекул - русалок, одна часть которых является гидрофильной (любит контактировать с водой), а другая гидрофобной (избегают подобного контакта, «боятся» воды). Гидрофильная часть представляет собой разделённые электрические заряды, она привлекается тонким слоем воды. В то время как гидрофобная – представляющая собой «хвост» из углеродной цепочки длиной 2,5 нм, наоборот, выталкивается. В результате образуются слои, защищающие воду от быстрого испарения, а также уменьшающие поверхностное натяжение.
Немногие знают, что плёнка мыльного пузыря представляет собой одну из самых тонких вещей, какие доступны невооружённому зрению. «Тонкий, как волос» - означают огромную толщину рядом с толщиной стенки мыльного пузыря, которая в 5000 раз тоньше волоса. Чтобы разрез стенки мыльного пузыря усматривался в виде тонкой линии необходимо увеличение в 40 000 раз, при таком же увеличении волос будет иметь толщину свыше 2 мм.
Поверхностное натяжение
Представьте себе каплю воды. Вода собирается на кончике пипетки в виде растущей капли, которая становится все больше и больше. Наконец она достигает определенного критического размера и отрывается от кончика пипетки. Впечатление такое, что вода стекает в маленький эластичный мешочек, наподобие воздушного шарика. Вокруг капли, естественно, нет никакого эластичного мешочка. Но что - то же должно удерживать каплю в ее классической форме? Должна же быть какая - то невидимая оболочка, какое - то нечто! Это нечто — свойство воды и любой другой жидкости называется поверхностным натяжением. Молекулы воды под ее поверхностью связаны между собой мощными силами межмолекулярного взаимодействия. Расположенные в поверхностном слое молекулы испытывают силу притяжения только со стороны нижележащих и соседних молекул, то есть они притягиваются внутрь и в стороны. Именно такое взаимодействие сил создает на поверхности воды эффект пленки, или поверхностное натяжение, которое можно рассматривать как своеобразную «оболочку» воды (рис.1). Наличие сил поверхностного натяжения делает поверхность жидкости похожей на упругую растянутую пленку.
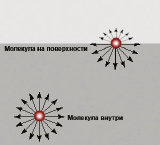
Рис. 1.
Шарообразная форма мыльного пузыря объясняется стремлением мыльной пленки сократиться до наименьших размеров. Такой формой является сфера, при этом давление внутри пузыря оказывается больше атмосферного. Избыточное давление обусловлено тем, что мыльная пленка, стремясь еще больше уменьшить свою поверхность, сдавливает воздух внутри пузыря, причем, чем меньше его радиус, тем большим оказывается избыточное давление внутри пузыря.
Интерференция света в тонких пленках
На первый взгляд, кажется, что мыльные пузыри бесцветные, но на самом деле, если присмотреться к нему получше, можно увидеть, что он переливается всеми цветами радуги. Переливчатые «радужные» цвета мыльных пузырей получаются за счёт интерференции световых волн и определяются толщиной мыльной плёнки (Приложение 1). Так как мыльный пузырь имеет форму сферы, то соответственно и две поверхности: внутреннюю и внешнюю.

Рис.2.
Когда свет проходит сквозь тонкую плёнку пузыря, часть его отражается от внешней поверхности, в то время как другая часть проникает внутрь плёнки и отражается от внутренней поверхности. Сначала плёнка бесцветная, так как имеет приблизительно равную толщину. Затем раствор постепенно стекает вниз. Из-за разной толщины нижней утолщённой и верхней утончённой плёнки появляется радужная окраска Более толстая плёнка убирает из белого света красный компонент, делая тем самым оттенок отражённого света сине-зелёным. Более тонкая пленка убирает жёлтый (оставляя синий свет), затем зелёный (оставляя пурпурный), и затем синий (оставляя золотисто-жёлтый) (рис.2).
Математика мыльного пузыря
Мыльные пузыри являются физической иллюстрацией проблемы минимальной поверхности, сложной математической задачи. Несмотря на то, что с 1884 года известно, что мыльный пузырь имеет минимальную площадь поверхности при заданном объёме, только в 2000 году было доказано, что два объединённых пузыря также имеют минимальную площадь поверхности при заданном объединённом объёме. Эта задача была названа теоремой двойного пузыря. С появлением геометрической теории меры удалось доказать, что оптимальная поверхность будет кусочно-гладкой, а не бесконечно изломанной. Когда два пузыря соединяются, они принимают форму с наименьшей возможной площадью поверхности. Их общая стенка будет выпячиваться внутрь большего пузыря, так как меньший пузырь имеет большую среднюю кривизну и большее внутреннее давление. Если пузыри одинакового размера, их общая стенка будет плоской. Правила, которым подчиняются пузыри при соединении, были экспериментально установлены в XIX веке бельгийским физиком Жозефом Плато и доказаны математически в1976 г. Жаном Тейлором. Если пузырей больше чем три, они будут располагаться таким образом, что возле одного края могут соединяться только три стенки, при этом углы между ними будут равны 120°, в силу равенства поверхностного натяжения для каждой соприкасающейся поверхности (рис.3).

Рис 3.
Поведение пересекающихся мыльных плёнок, можно исследовать, меняя положение в пространстве двух простых плоских рамок. При погружении объемных рамок в мыльный раствор, получаются удивительные по красоте и форме пленки. Казалось бы, должны получаться пленки, обтягивающие каркас. Но нет! В случае куба, тетраэдра, четырехугольной пирамиды и многих других фигур, пленки прикрепляются к ребрам и сходятся внутри. Площадь пленок, натянутых на каркас, всегда минимальна.
С помощью рамок можно наглядно решать некоторые геометрические и архитектурные задачи. При проектировке зданий крыши макетов выполняются в виде каркасов. Расчет проверяется с помощью мыльных пленок, которые формируются на этих рамках. (Приложение 2)
Практическая часть
Исследование физических свойств мыльного пузыря
Скажи мне, и я забуду.
Покажи мне, и я запомню.
Дай мне действовать самому, и я научусь.
Конфуций
Правила по технике безопасности:
1. Работать с раствором надо очень аккуратно, хранить в закрытом сосуде.
2. Освещение должно быть, по возможности, яркое: иначе пузыри не покажут своих радужных переливов.
3. Производить опыты нужно медленно, осторожно, спокойно.
4. Раствор не должен быть слишком вспененным. Если у Вас образуется много пены на поверхности раствора, просто снимите ее рукой или сдуйте.
5. После работы вымыть руки.
Оборудование:



– Мыльный раствор (Приложение 3)
– Устройство для надувания пузырей (соломинка, воронка)
– Кольца для выдувания пузырей разного диаметра
– Проволочные рамки каркасов в форме различных геометрических фигур
– Штангенциркуль
– П-образный каркас из проволоки с подвижной перекладиной; две прямые проволочки диаметром 0,3 мм и длиной приблизительно 50 мм, проволочный каркас в виде кольца, иголка, скрепка
– Фотоаппарат
Эксперимент №1. Обнаружение поверхностного натяжения
Цель: показать на опыте, что жидкость имеет поверхностное натяжение, убедиться в упругости поверхностной пленки.
1. Проволочное кольцо нужно окунуть в мыльный раствор, на нем образуется мыльная пленка. Свернуть из кусочка нитки петельку, смочить ее мыльным раствором и аккуратно положить ее на пленку. Прикоснуться каким- либо предметом к мыльной пленке внутри петельки -она лопнет, а та, что осталась снаружи, растянет нитку в красивое кольцо. Это кольцо будет растягиваться натяжением мыльной пленки, оставшейся между краем петли и мыльным кольцом».


2. На поверхность воды положить иголку, скрепку.


3. Устроить «Водопад через мыльную пленку»: прохождение струи воды через мыльную пленку, которая при этом остается целой и невредимой.
4. Используя трансформирующиеся модели из комплекта по стереометрии можно наблюдать, как пленка растягивается, но не рвется при преобразовании одной фигуры в другую, например, взять фигуру – четырехугольная пирамида .


Мыло уменьшает поверхностное натяжение воды, а глицерин – уплотняет ее. Это позволяет получить очень тонкую стенку мыльного пузыря. Она легко растягивается, но не рвется. Она довольно прочная, учитывая ее толщину.
Вывод: Эти опыты убеждают в наличии поверхностного натяжения. Наличие поверхностного натяжения делает поверхность жидкости похожей на упругую растянутую пленку. Стенка мыльного пузыря входит в число тех немногих микроскопических объектов, которые можно увидеть невооруженным глазом.
Эксперимент№2. Измерение сил поверхностного натяжения
Цель: исследовать зависимость силы поверхностного натяжения от длины линии, разделяющей поверхности жидкости и твердого тела.
Проводим эксперимент с проволокой разной длины(5 см и 9 см)
1. Зацепить самую короткую тонкую проволочку, чуть изогнутую по краям, чувствительным пружинным динамометром (ц.д.=0,02Н) и опустить в воду. Очень медленно, без толчков поднимать проволочку. Когда показание динамометра достигнут максимального значения, зафиксировать это показание.

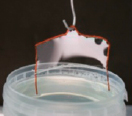
2. Заменить короткую проволоку на длинную и повторить опыт. Зафиксировать показание динамометра.
Вывод: Сила поверхностного натяжения прямо пропорциональна длине линии, разделяющей поверхность жидкости и соприкасающегося с ней тела: чем больше длина проволоки, тем больше сила поверхностного натяжения.
Эксперимент№3. Измерение коэффициента поверхностного натяжения
Цель: измерить коэффициент поверхностного натяжения мыльного раствора.
Физическую величину, равную отношению силы поверхностного натяжения к длине линии, ограничивающей поверхность жидкости, называют коэффициентом поверхностного натяжения.
Динамический метод Сталагмометрический, или метод счета капель.
В основе расчетов лежит закон, согласно которому вес капли, отрывающейся от пипетки равен силе поверхностного натяжения жидкости. (Приложение 4)
|
|
количество капель n |
масса пустого стаканчика М1 |
масса стаканчика с водой М2 |
М – масса жидкости |
диаметр отверстия трубки D |
g – ускорение силы тяжести |
Н/м |
|
60 |
0.028 |
0,031 |
0,003 |
0,004 |
9,8 |
0.039 |
Статический метод: Метод поднятия в капилляре
Чем меньше радиус капилляра r0, тем на большую высоту поднимается в ней жидкость. (Приложение 5)
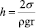
|
|
ρ=m/v, кг/м3 |
r, м |
h, м |
g, Н/кг |
σ=pgh/2, Н/м |
Табличное значение |
|
1005 |
0,0025 |
0,003 |
9,8 |
0,037 |
0,040 |
Эксперимент №4. Наблюдение сокращения пленки до наименьших размеров или Почему пузырь круглый?
Цель: проверить опытным путем, что если на жидкость не действуют другие силы или их действие мало, то жидкость будет стремиться принимать сферическую форму ив свободном состоянии будет стремиться сделать свою поверхность минимальной.




1. Образуем мыльную пленку на кольце с ниткой. Поверхность «туго» натянута. Пока пленка цела по обе стороны нитки, нитка имеет свободную форму. Если уничтожить пленку по одну сторону нитки, то мыльная пленка по другую сторону тотчас уменьшит свою поверхность и натянет нитку.
2. Опускаем рамку в мыльный раствор, а затем вынимаем ее оттуда и видим тонкую радужную пленку, которая закрывает просвет рамки. Подуем на рамку. Из нее начнет выпячиваться пузырь. Мыльная пленка растягивается наподобие эластичной оболочки. Подуем еще. Мыльная пленка сомкнется вокруг воздуха, и мыльный пузырь отправится в самостоятельное путешествие, переливаясь всеми цветами радуги.
Вывод: В эксперименте видно стремление пленки сократиться до наименьших размеров. Мыльный пузырь в свободном состоянии может принимать только форму сферы с наименьшей площадью поверхности. Силы поверхностного натяжения стремятся придать мыльному пузырю максимально компактную форму, а это сферическая форма.
Эксперимент №5 Электрические свойства мыльного раствора
Цель: обнаружить на опыте электропроводность, убедиться на опыте, что мыльные пузыри электризуются, электрическое поле действует на раствор.
Оборудование: набор лабораторного оборудования по электричеству, дистиллированная вода, мыльный раствор, емкость.
1. Собрать электрическую цепь, состоящую из источника тока, лампочки, кюветы с жидкостью, ключа.


2. В бутылке сделаем отверстие (прокол) и нальем раствор. Он будет вытекать тоненькой струйкой. Поднесем наэлектризованную палочку к струйке. Струйка будет притягиваться к наэлектризованной палочке.



4. На ворсистых поверхностях всегда есть некоторый электростатический заряд. Когда пузырь падает на такую поверхность, он может пружинить на ней как мячик, даже можно поиграть им, подкинув его несколько раз. Мыльные пузыри очень лёгкие, поэтому возникающего (хоть и очень слабого) электростатического разряда между пузырём и ворсистой поверхностью хватает для того, чтобы пузырь на неё не опускался. Так как пузырь не успевает коснуться ворсистой поверхности из-за действия сил электростатического отталкивания, то он и не лопается.
Вывод: В результате эксперимента мы убедились в плохой проводимости воды (лампочка не загорелась), при помещении электродов в сосуд с мыльным раствором наблюдалось свечение лампочки, следовательно, можно утверждать, что мыльный раствор - проводник. Электрическое поле действует на пузырь - вытягивание его в эллипсоид и на струйку – она притягивается к палочке.
Эксперимент№6. Наблюдение интерференции света на мыльных пузырях
Цель: Переливчатые «радужные» цвета мыльных пузырей получаются за счёт интерференции световых волн и определяются толщиной мыльной плёнки.




Вывод: Пузырь кажется нам разноцветным и радужным из-за физического явления — интерференции. Солнечные лучи преломляются и переливаются разными цветами радуги.
Эксперимент№7. Математика мыльных пузырей. Соединение пузырей
1. Проверить на опыте, что если пузырей больше чем три, они будут располагаться таким образом, что возле одного края могут соединяться только три стенки, при этом углы между ними будут равны 120°, в силу равенства поверхностного натяжения для каждой соприкасающейся поверхности. (Приложение 4)
2. Проверить на опыте, что давление внутри пузыря больше атмосферного. Избыточное давление обусловлено тем, что мыльная пленка, стремясь еще больше уменьшить свою поверхность, сдавливает воздух внутри пузыря, причем, чем меньше его радиус, тем большим оказывается избыточное давление внутри пузыря.


3. Проверить на опыте, что когда два пузыря соединяются, они принимают форму с наименьшей возможной площадью поверхности. Их общая стенка будет выпячиваться внутрь большего пузыря, так как меньший пузырь имеет большую среднюю кривизну и большее внутреннее давление. Если пузыри одинакового размера, их общая стенка будет плоской.


4. При погружении объемных рамок в мыльный раствор, получаются удивительные по красоте и форме пленки. В случае куба, тетраэдра, четырехугольной пирамиды и многих других фигур, пленки прикрепляются к ребрам и сходятся внутри. Площадь пленок, натянутых на каркас, всегда минимальна. Если дотронуться палочкой, смоченной в мыльном растворе до поверхности любой пленки и потянуть к другой плёнке, то палочка не разорвёт плёнку, а соединит плёнки между собой. Таким образом, можно получать разные плёночные поверхности. Это происходит, потому что мыльная пленка, образованная на палочке, не разрывает поверхность мыльной плёнки, а дополняет и подпитывает ее: они как- бы срастаются!
Вывод: Опыт показывает устойчивость мыльной пленки, образующейся под действием сил сцепления между молекулами мыльного раствора. Мыльные плёнки существуют благодаря торможению их границами стекающего мыльного раствора, для чего необходима жёсткость этих границ. Устойчивость мыльных плёнок объясняется, тем, что они имеют эластичность, они способны растягиваться и упруго сокращаться. Мыльные пленки образуют такие фигуры, которые имеют наименьшую общую поверхность.
Эксперимент№8.Заморозка мыльного пузыря
Цель: проверить на опыте, что мыльный пузырь при медленном охлаждении переохлаждается и замерзает примерно при –7°C.



Вывод: При низкой температуре мыльный пузырь покрывается тончайшей ледяной корочкой, наблюдаются вмятины, пленка оказывается не хрупкой, она обнаруживает пластичность, отдельные обломки закручиваются в трубочки, падая на землю - разбивается.
Эксперимент№9. Невероятные свойства мыльного пузыря
Цель: продемонстрировать невероятные свойства мыльного пузыря.
Вывод: Проделанные опыты опровергают распространенное убеждение о недолговечности мыльного пузыря, иллюстрируют необыкновенные свойства мыльных пузырей: прочность, эластичность и красоту.
Результаты исследования:
В ходе выполнения работы мы провели много экспериментов, все поставленные задачи выполнили, гипотеза подтвердилась:
– Мыльная пленка является прекрасным объектом для изучения его физических свойств.
– Переливы красок на поверхности тончайших мыльных пленок дают физику возможность измерить длину световых волн, а исследование натяжения пленок помогает изучать законы действия сил между частицами - тех сил сцепления, при отсутствии которых в мире не существовало бы ничего, кроме тончайшей пыли. Объяснить радужную окраску мыльных пузырей можно на основе интерференции света на тонких пленках.
– Необыкновенно интересные опыты с мыльными пузырями могут превратиться в грандиозное шоу, а уменье выдувать большие и красивые пузыри - своего рода искусство.
– Подготовили материал для демонстрации на уроках физики, математики и во внеклассной работе.
– Провели мастер-класс на общешкольном родительском форуме «Большая перемена», на классном часе удивили первоклассников – продемонстрировали необычайные опыты с мыльными пузырями.
|
Пузыри один в другом «Матрешка».
|
Пузыри на предметах.
|
Пузырь на ладони
|
|
«Рука в мыльном пузыре»
|
«Человек в мыльном пузыре»
|
|
|
Мыльные цветы.
|
||
Заключение
Пуская мыльные пузыри, имеешь дело с очень интересным физическим объектом, изучая свойства которого, лучше узнаёшь законы мира, в котором мы живём.
Выполненная нами работа показала, как много можно узнать о «простом» мыльном пузыре, который, с первого взгляда, кажется всего лишь детской забавой. Мы заглянули в суть процесса, ведь силы поверхностного натяжения играют большую роль в окружающей природе и жизни человека. Без них невозможны многие физические явления, достаточно упомянуть каплю воды, свисающую из крана или водомерку на глади пруда. Интерференция не только раскрашивает мыльные пузыри,но и помогает оценить толщину материала с такой точностью, которой нет у других измерительных приборов, она позволяет заглянуть в суть строения вещества и осознать размеры молекулы.
Слова английского учёного лорда Кельвина «Выдуйте мыльный пузырь и смотрите на него: вы можете заниматься всю жизнь его изучением, не переставая извлекать из него уроки физики» говорят мне, что, несмотря на большое количество разного рода сведений о мыльных пузырях, обязательно найдутся «белые пятна», требующие дальнейших исследований. Есть много других, не рассмотренных в данной работе, задач о мыльных пузырях, экспериментальных и теоретических. А это значит - работа продолжается.
Приложение 1
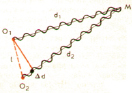
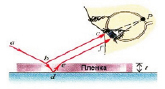
Явление интерференции - перераспределение интенсивности (энергии) света в результате наложения нескольких когерентных световых волн, которое сопровождается чередующимися в пространстве максимумами и минимумами интенсивности. Когерентные волны – это волны, имеющие одинаковую частоту и постоянную во времени разность фаз. Данная тема изучается лишь в 11 классе, но мы решили углубиться в этот материал и включить его в свою работу, т.к. интерференция света является одним из важнейших свойств мыльной пленки.
Условие максимума: если разность хода двух волн, возбуждающих колебания в этой точке, равна целому числу длин волн Δd = kλ , k =0,1,2,3,… - волны усилят друг друга, Δd – разность хода лучей.
Условие минимума: если разность хода двух волн, возбуждающих колебания в этой точке, равна нечётному числу полуволн Δd =(2k+1) λ/2 , k =0,1,2,3,… -волны погасят друг друга.
Приложение 2
Формы мыльных пузырей – геометрические фигуры
|
Цилиндрическая форма Два одинаковых кольца с мыльной пленкой соединяют, а затем растаскивают. Центральную пленку прокалывают.
|
Трехлопастная рамка Углы между лопастями объемной тройной рамки влияют на линию пересечения пленок. Вид линии – дуга окружности.
|
Тетраэдрическая форма Внимательно наблюдайте за пленками на рамках. Когда лопается одна из них, все пленки самопроизвольно перестраиваются!
|
|
Шестиугольная пирамида В случае шестиугольной пирамиды пленки образуются на гранях пирамиды, но основание никогда не затягивают.
Пленки на плоских рамках
|
Спираль Необходимое условие для получения мыльных пленок – замкнутость каркаса, поэтому необходимо соединить первый и последний виток осью (стержнем). Ось не обязательно должна проходить по центру, ее задача - замкнуть рамку.
|
Квадратная пирамида
Пересечение рамок
|
Приложение 3
Рецепты раствора для мыльных пузырей
Раствор №1. На 200 гр. средства для мытья посуды взять 600 мл. воды и 100 мл. глицерина. Всё хорошенько размешать и ваш раствор готов. Глицерин добавляют для увеличения полярности длинных молекул растворителя, один из концов которых (гидрофильный) любит воду, а другой (гидрофобный) предпочитает жир. В результате в двойной мыльной пленке все водолюбивые хвосты молекулы мыла ориентированы внутрь пленки, водоотталкивающие — наружу.
Глицерин именно то средство, которое делает стенки мыльного пузыря прочнее, а сам пузырь более долгоживущим.
Раствор №2. На 600 мл. горячей воды нужно взять 300 мл. глицерина, 20 капель нашатырного спирта и 50 гр. любого порошкообразного моющего средства. Все ингредиенты перемешиваем и оставляем настояться на 2-3 дня. После этого раствор тщательно профильтровываем и ставим в холодильник на 12 часов.
Раствор №3. 600г воды +200г жидкого моющего средства для посуды + 100г глицерина
Раствор№4600г горячей дистиллированной воды + 300г глицерина + 50г моющего средства в порошке + 20 капель нашатырного спирта. (Раствор должен настояться несколько дней, потом его надо отфильтровать и перед употреблением поставить на 12 часов в холодильник) .5. 4ст. ложки мыльной стружки растворить в 400г горячей воды (лучше это делать на огне). Дать постоять неделю. После этого добавить 2ч. ложки сахара.
Приложение 4
1. Сталагмометрический метод (Метод счета капель) При выполнении работы использовался метод счета капель. В основе расчетов лежит закон, согласно которому вес капли, отрывающейся от пипетки равен силе поверхностного натяжения жидкости:
Метод измерения коэффициента поверхностного натяжения жидкости основывается на наблюдении истечения жидкости из малого отверстия в сосуде. Бюретка (от англ. burette) — тонкая проградуированная стеклянная трубка ёмкостью обычно 50 мл, открытая на одном конце и снабжённая стеклянным или тефлоновым запорным краном на другом. Предназначена для точного измерения небольших объемов жидкости. На конце бюретки находится наконечник-трубка, на конце которой образуется капля.

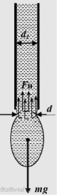
Оборудование: Установка для измерения коэффициента поверхностного натяжения (штатив, бюретка), электронные весы, стаканчик, штангенциркуль, секундомер.
1. С помощью штангенциркуля измеряют диаметр наконечника-трубки три раза и вычисляют среднее значение D.
2. Закрывают кран и наливают воду.
3. Подставляют под трубку колбу и, приоткрывая кран, добиваются, чтобы капли падали достаточно медленно (10 – 15 капель в минуту). Тогда можно считать, что отрывание капель происходит только под действием веса.
4. Отсчитывают точно количество отлитых капель из бюретки в стаканчик (60 капель) и перекрывают кран.
8. Подставляя полученные значения в формулу, вычисляют коэффициент поверхностного натяжения в системе СИ (Н/м). 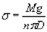
Приложение 5
2. Статический метод: Метод поднятия в капилляре
Формула Жюрена (формула Борелли — Жюрена) — формула, определяющая высоту поднятия жидкости в капиллярах. Названа в честь Дж. Жюрена и Дж. Борелли, которые экспериментально установили некоторые закономерности капиллярного поднятия соответственно в 1717 и 1670 гг. Чем меньше радиус капилляра r0, тем на большую высоту поднимается в ней жидкость. Высота поднятия столба жидкости растет также с увеличением коэффициента поверхностного натяжения жидкости.
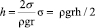
Оборудование: Установка для измерения коэффициента поверхностного натяжения капилляр, штангенциркуль, емкость с раствором, линейка.
1. Налить раствор в стакан
2. Собрать установку
3. Поместить капилляр в сосуд
4. Занести в таблицу значение высоты поднятия жидкости в капилляре
5. Опыт повторить 3 – 4 раза.
6. Вычислить плотность раствора( измерить массу и объём жидкости) по формуле
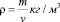
7.Рассчитать коэффициент поверхностного натяжения по формуле. (Значение диаметра капилляра d измерить с помощью штангенциркуля)
Библиографическая ссылка
Денисова Б.С. ИССЛЕДОВАНИЕ ФИЗИЧЕСКИХ СВОЙСТВ МЫЛЬНОГО ПУЗЫРЯ // Международный школьный научный вестник. 2017. № 4. ;URL: https://school-herald.ru/ru/article/view?id=326 (дата обращения: 13.02.2026).