Целью работы является изучение связи между искусством и математическими науками, а также изучение и анализ различных сфер применения математических знаний в изобразительном искусстве. Объект исследования – основы применения математических методов в изобразительном искусстве. Предмет исследования – использование тесселяции, анаморфного изображения, невозможных фигур и фракталов при создании картин. На основании теоретического анализа литературы и ранее проведенных исследований была сформулирована гипотеза: математические методы построения трехмерного пространства на плоскости являются неотъемлемой частью композиции картины.
Для достижения цели и решения поставленных задач применен комплекс методов исследования: изучение и анализ литературы и научно-исследовательских работ по теме исследования; теоретический анализ, проведение опытно-экспериментальной работы.
В соответствии с поставленной целью решались следующие основные задачи:
1. Изучить связь между искусством и математическими науками и понять важность математических законов и расчетов.
Своеобразие геометрии, выделяющее ее из других разделов математики, да и всех областей науки вообще, заключается в не разрывном, органическом соединении живого воображения со строгой логикой. В своей сущности и основе геометрия и есть пространственное воображение, пронизанное и организованное строгой логикой. В ней всегда присутствуют эти два неразрывно связанных элемента: наглядная картина и точная формулировка, строгий логический вывод. Там, где нет одной из этих сторон, нет и подлинной геометрии.
2. С математической точки зрения рассмотреть подробно некоторые из видов изобразительного искусства, а именно: невозможные фигуры, фракталы, тесселяция, а также анаморфные изображения.
Рассмотрим наиболее часто используемые в изобразительном искусстве математические основы создания картин [4].
Тесселяция означает мозаика. При тесселяции плоскость картины разбивается на фрагменты, которые заполняют ее без накладок и пробелов. Регулярное разбиение плоскости, называемое «мозаикой» – это набор замкнутых фигур, которыми можно замостить плоскость без пересечений фигур и щелей между ними.
Невозможные фигуры – эти фигура, изображенная в перспективе таким способом, чтобы выглядеть на первый взгляд обычной фигурой. Однако при более внимательном рассмотрении зритель понимает, что такая фигура не может существовать в трехмерном пространстве. Все объекты, нарисованные на бумаге, являются проекциями трёхмерных объектов, следовательно, можно создать такой трёхмерный объект, который при проецировании на плоскость будет выглядеть невозможным. При взгляде на такой объект из определённой точки он также будет выглядеть невозможным, но при обзоре с любой другой точки эффект невозможности будет теряться.
Фрактал – математическое множество, обладающее свойством самоподобия (объект, в точности или приближённо совпадающий с частью себя самого, то есть целое имеет ту же форму, что и одна или более частей).
Анаморфные изображения – это умышленно искаженные изображения, которые представляются правильными только при рассмотрении их с определенного ракурса или под определенным ракурсом.
3. Используя математические навыки, самостоятельно создать тесселяционное изображение, анаморфное изображение, невозможный треугольник и фракталы.
Практическая работа заключалась в создании изображений на листе бумаги.
Создание тесселяции.
С помощью созданного алгоритма создания тесселяции и проделанных мною исследований построили собственную тесселяцию в виде бабочек. При изучении тесселяционных изображений было установлено, что построение тесселяции начинается с фрагмента, который впоследствии повторяется; фрагмент в любой тесселяции начинает формироваться из третьего ряда; тесселяция строится по принципу мозаики; при разбиении правильного n-угольника формируется n одинаковых фигур (рис. 1).
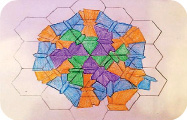
Рис. 1. Тесселяция
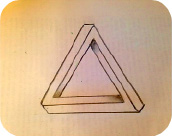
Рис. 2. Невозможная фигура
Исследование и создание невозможных фигур
После построения невозможного треугольника было замечено: иллюзия невозможности существования в трехмерном пространстве любой нормальной объемной фигуры может быть достигнута путем полного или частичного проецирования точек поверхности объемной фигуры на плоскость в обратном порядке, т.е. путем отображения на плоскость ближних к наблюдателю точек первыми, а дальних последними. Или можно сказать иначе – путем изменения окраски трехмерной модели отображаемой на плоскость геометрической фигуры. Для получения иллюзии невозможности существования в трехмерном пространстве какой-либо геометрической фигуры вовсе не обязательно делать в ее трехмерной модели, как в реальной, так и в виртуальной, какие-либо прорези и изгибы, скрываемые от наблюдателя. В качестве трехмерной модели любой невозможной фигуры всегда можно использовать нормальную, без каких-либо геометрических деформаций, объемную геометрическую фигуру, т.е. нормальные геометрически не измененные треугольники, прямоугольники, кольца, кубы и т.д. (рис. 2).
Создание фрактального рисунка
Фракталы этого типа строятся поэтапно. Сначала изображается основа. Затем некоторые части основы заменяются на фрагмент. На каждом следующем этапе части уже построенной фигуры, аналогичные замененным частям основы, вновь заменяются на фрагмент, взятый в подходящем масштабе. Всякий раз масштаб уменьшается. Когда изменения становятся визуально незаметными, считают, что построенная фигура хорошо приближает фрактал и дает представление о его форме. Для получения самого фрактала нужно бесконечное число этапов. Меняя основу и фрагмент, можно получить много разных геометрических фракталов (рис. 3).

Рис. 3. Фракталы

Рис. 4. Анаморфное изображение
Исследование и построение анаморфной сетки
После проделанных мною опытов было установлено, что построение анаморфной сетки не зависит от диаметра цилиндра и то, что прямые линии сетки исходят из центра окружности под равными углами относительно друг друга, разбивая плоскость на равные части. Изображение, нарисованное искаженно в анаморфоскопе имеет правильную форму (рис. 4).
Применение
Применение различных математических методов в искусстве очень широко. Творчество М.К. Эшера оказало значительное влияние на развитие такого творчества как лоскутное шитье-пэчворк [6].
Вместе с моей мамой мы сшили покрывало на основе пэчворка с применением методов тесселяции (рис. 5).

Рис. 5. Покрывало в стили пэчворк
Заключение
Математическое изобразительное искусство процветает сегодня. Художники работают в различных направлениях, включая скульптуру, рисование на плоских и трехмерных поверхностях, литографию и компьютерную графику. Наиболее популярными темами математического искусства остаются многогранники, тесселяции, невозможные фигуры, ленты Мебиуса, искаженные системы перспективы и фракталы [2].
В данной работе рассмотрено лишь несколько работ художника математического изобразительного искусства Маурица Корнелиса Эшера [5]. Математика – это не только стройная система законов, теорем, задач, но и уникальное средство познания красоты. А красота многогранна и многолика. Она выражает высшую целесообразность устройства мира, подтверждает универсальность математических закономерностей, которые действуют одинаково эффективно в кристаллах и в живых организмах, в атомах и во Вселенной, в произведениях искусства и научных открытиях.
Красота помогает с радостью воспринимать окружающий мир, математика даёт возможность осознать явления и упрочить знания о гармонии всего мира.
Многие художники в своих работах используют математику. В своей работе я постаралась, и надеюсь, доказала, что, казалось бы, такие отдалённые дисциплины как математика и изобразительное искусство пересекаются друг с другом, а в творчестве некоторых художников они очень тесно связаны.
В ходе исследования выяснилось, что зрение человека не всегда дает ему точные сведения о реальных предметах и тому подтверждение геометрически парадоксальные картины М. Эшера. Используя только зрение, человек легко может обмануться, а математика изучает реальный мир и реальные объекты, отраженные в нашем сознании, исходя из их свойств.
Метод, применяемый при изучении чисел и геометрических фигур (метод математического мышления), пригоден не только для нужд математики, но и помогает художникам изображать красоту мира.
В своей работе я рассмотрела только несколько законов математики, применяемых живописцами. Но этого уже достаточно, чтобы убедиться во взаимосвязи двух на первый взгляд несовместимых понятий: математика и изобразительное искусство.
Математика не только «ум в порядок приводит», но и несет в себе большой эстетический потенциал в развитии различных видов искусства, являясь «царицей всех наук».
Библиографическая ссылка
Кенжина А.А. МАТЕМАТИЧЕСКИЕ ОСНОВЫ В ИЗОБРАЗИТЕЛЬНОМ ИСКУССТВЕ // Международный школьный научный вестник. 2016. № 2. ;URL: https://school-herald.ru/ru/article/view?id=33 (дата обращения: 29.01.2026).
