Данная статья является реферативным изложением основной работы. Полный текст научной работы, приложения, иллюстрации и иные дополнительные материалы доступны на сайте III Международного конкурса научно-исследовательских и творческих работ учащихся «Старт в науке» по ссылке: https://www.school-science.ru/0317/7/29073.
«То, что мы знаем – ограничено»,
а то, что мы не знаем – бесконечно»
П. Лаплас
Математики во все времена мечтали о таком помощнике, который освободил бы их из плена долгих и утомительных вычислений. Сегодня такой помощник существует – это микрокалькулятор. Микрокалькулятор позволяет проводить вычисления чрезвычайно быстро: то, что раньше требовало многочасовой кропотливой работы, теперь может быть проделано за несколько минут. Для записи любого числа в десятичной системе счисления мы используем только десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, которые расположены на клавиатуре микрокалькулятора и составляют числовой массив, в котором очевидны закономерности: в строке каждое следующее число на 1 больше предыдущего; в столбце каждое следующее число больше предыдущего на 3 (клавишу с цифрой 0 условимся не рассматривать) [3, с. 6].
|
7 |
8 |
9 |
|
4 |
5 |
6 |
|
1 |
2 |
3 |
Возникают вопросы: Существуют ли другие закономерности чисел, расположенных на клавиатуре микрокалькулятора? Может ли микрокалькулятор служить инструментом изучения свойств чисел?
Поскольку у нас нет полного понимания и ответов на поставленные вопросы, имеет место противоречие: с одной стороны мы видим, что микрокалькулятор кажется таким простым, с другой стороны – сколько разных значений имеет!? И скорее всего, имеются закономерности, связанные с расположением чисел на клавиатуре.
С учётом выявленного противоречия была сформулирована проблема: каковы закономерности чисел, расположенных на клавиатуре микрокалькулятора?
Выявленный недостаток в наших знаниях и понимании по данному вопросу сделал для нас актуальной эту проблему и вызвал необходимость разрешить возникшее противоречие.
Актуальность проблемы и недостаточное понимание вопроса определили тему нашего исследования: «Микрокалькулятор: закономерности чисел, расположенных на клавиатуре».
Цель исследования: выявление закономерностей чисел, расположенных на клавиатуре микрокалькулятора.
Объект исследования: Натуральные числа от одного до девяти, расположенные на клавиатуре микрокалькулятора.
Предмет исследования: Закономерности чисел, расположенных на клавиатуре микрокалькулятора.
Гипотеза исследования: так как на клавиатуре микрокалькулятора расположены только цифры, которые мы используем для записи любого числа в десятичной системе счисления и расставлены они строго по порядку, то в образованном числовом массиве существуют определенные числовые закономерности.
Задачи исследования:
1. ознакомиться с источниками, содержащими сведения по теме исследования;
2. исследовать закономерности, зависящие от расположения натуральных чисел на клавиатуре микрокалькулятора; проанализировать выявленные закономерности, выяснить, обнаруживаются ли в исследуемом массиве чисел закономерности стоклеточного квадрата;
3. исследовать закономерности, не зависящие от расположения натуральных чисел на клавиатуре микрокалькулятора; проанализировать выявленные закономерности;
4. сделать вывод по проделанной работе;
5. создать проект учебного пособия «Микрокалькулятор: закономерности чисел расположенных на клавиатуре. Исследовательские задачи по математике».
Этапы исследования:
1-й этап – подготовительный – включал обоснование актуальности исследования, выявление проблемы, определение объектной области, объекта и предмета исследования, выбор темы, изучение литературы и уточнение формулировки темы, формулирование гипотезы, формулирование цели и задач исследования;
2-й этап – собственно исследование – состоял в исследовании числовых закономерностей, как зависящих от расположения цифр на клавиатуре, так и не зависящих от этого;
3-й этап – аналитический – включал анализ проделанной работы и создание проекта учебного пособия «Микрокалькулятор: закономерности чисел расположенных на клавиатуре. Исследовательские задачи по математике» в виде тетради с печатной основой, использование которой возможно при изучении натуральных чисел на уроках математики, а также на занятиях по внеурочной деятельности.
Закономерности, зависящие от расположения чисел на клавиатуре микрокалькулятора
Числа на клавиатуре микрокалькулятора расположены в определенном порядке (в строке каждое следующее число на 1 больше предыдущего, в столбце каждое следующее число больше предыдущего на 3) и образуют числовой массив (рис. 1).
|
7 |
8 |
9 |
|
4 |
5 |
6 |
|
1 |
2 |
3 |
Рис. 1.
Равенство сумм четвёрок чисел. Легко заметить, что суммы отмеченных на рис. 2–4 чисел одинаковы и равны двадцати. При исследовании различных комбинаций четверок чисел, дающих сумму двадцать, найдено двенадцать вариантов (Приложение I).
|
7 |
8 |
9 |
|
4 |
5 |
6 |
|
1 |
2 |
3 |
Рис. 2
|
7 |
8 |
9 |
|
4 |
5 |
6 |
|
1 |
2 |
3 |
Рис. 3
|
7 |
8 |
9 |
|
4 |
5 |
6 |
|
1 |
2 |
3 |
Рис. 4
Равенство сумм троек чисел. Суммы отмеченных рис. 5–7 чисел одинаковы и равны пятнадцати. Исследование различных комбинаций троек чисел, дающих сумму пятнадцать, показало: существует, по крайней мере, восемь таких вариантов (Приложение II).
|
7 |
8 |
9 |
|
4 |
5 |
6 |
|
1 |
2 |
3 |
Рис. 5
|
7 |
8 |
9 |
|
4 |
5 |
6 |
|
1 |
2 |
3 |
Рис. 6
|
7 |
8 |
9 |
|
4 |
5 |
6 |
|
1 |
2 |
3 |
Рис. 7
Перебирая различные комбинации чисел, дающих одинаковую сумму в исследуемом массиве, замечено, что если найден один из вариантов, то легко найти второй – он симметричен первому, как показано на рис. 8–9.
|
7 |
8 |
9 |
|
4 |
5 |
6 |
|
1 |
2 |
3 |
Рис. 8
|
7 |
8 |
9 |
|
4 |
5 |
6 |
|
1 |
2 |
3 |
Рис. 9
Это можно объяснить тем, что в десятичной системе счисления сумма не изменяется тогда, когда к одному из слагаемых прибавляется некоторое число, а из второго слагаемого вычитается это же число:
а+в = (а+2)+(в-2)
(Например, 3+4 = (3+2)+(4–2) = 5+2).
В нашем случае:
1+4+6+9 = (1+2)+4+6+(9–2) = 3+4+6+7
Возможно, существуют ещё варианты, нам не удалось найти формулу для точного подсчета количества имеющихся вариантов. Была попытка связать нашу задачу с комбинаторными задачами [1, с. 347]. На первый взгляд исследование различных четверок (троек) чисел, дающих одинаковую сумму в квадрате три на три – есть задача комбинаторики («особая примета» комбинаторных задач – перебор вариантов), но мы не нашли с ними связи, так как комбинаторные задачи предполагают перестановки одних и тех же элементов, а в нашем случае числа разные, а сумма одинаковая.
Очевидны следующие закономерности…
Равенство разностей трёхзначных чисел, составленных из цифр, расположенных по соседним вертикальным линиям. Разность чисел, составленных из цифр, расположенных по соседним вертикальным линиям равна 111 (рис.10), т.к. каждое следующее число в строке на 1 больше предыдущего:
а) 963 – 852 = 111;
б) 852 – 741 = 111;
в) 258 – 147 = 111;
г) 369 – 258 = 111.
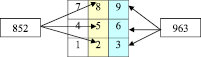
Рис. 10
Равенство разностей трёхзначных чисел, составленных из цифр, расположенных по соседним горизонтальным линиям. Разность чисел, составленных из цифр, расположенных по соседним горизонтальным линиям равна 333 (рис.11), т.к. каждое следующее число в столбце на 3 больше предыдущего:
а) 789 – 456 = 333;
б) 456 – 123 = 333;
в) 654– – 321 = 333;
г) 987– 654 = 333.
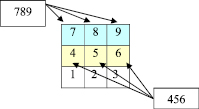
Рис. 11
…Другие закономерности более удивительны.
Равенство разностей двузначных обращённых чисел, составленных из цифр, расположенных по вертикальным линиям. Возьмем двузначное число, составленное из цифр, расположенных по вертикальной линии, например 74. Поменяем цифры местами – 47 (Обращенное число – число, записанное теми же цифрами, но в обратном порядке) [3,с. 7] и вычтем полученное число из 74 (рис. 12). Получим 27. Составим аналогичные разности, исследуем, всегда ли разность составляет 27?
а) 74 – 47 = 27;
б) 85 – 58 = 27
в) 96 – 69 = 27;
г) 41 – 14 =27;
д) 52 – 25 = 27;
е) 63 – 36 = 27.
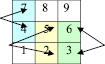
Рис. 12
Результат всегда – 27: в разности двузначных чисел, составленных из цифр, расположенных по вертикальной линии количество десятков и количество единиц отличается на 3, значит, разность равна 30 – 3 = 27.
Составив разности следующим образом: 71–17; 82–28; 93–39 и вычислив их, замечаем, что разность всегда равна 54 (количество десятков и количество единиц в числах отличается на 6, значит, разность равна 60 – 6 = 54).
Равенство разностей двузначных обращённых чисел, составленных из цифр, расположенных по горизонтальным линиям. Возьмем двузначное число, составленное из цифр, расположенных по горизонтальной линии, например 98. Вычтем из него обращенное число – 89 (рис.13). Получим 9. В аналогичных разностях результат всегда равен 9, т.к. количество десятков и количество единиц отличается на 1, значит, разность равна 10–1=9.
а) 98 – 89 = 9;
б) 87 – 78 = 9;
в) 65 – 56 = 9;
г) 54 – 45 =9;
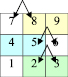
Рис. 13
Составив разности: 97–79; 64–46; 31–13 и вычислив их замечаем, что разность всегда равна 18 (количество десятков и количество единиц в числах отличается на 2, значит разность равна 20 – 2 = 18).
Равенство разностей трёхзначных обращённых чисел, составленных из цифр, расположенных по вертикальным линиям. Возьмем трехзначное число, составленное из цифр, расположенных по вертикальной линии, например 741. Вычтем из него обращенное число – 147. Получим 594 (рис.14).
а) 741 – 147 = 594;
б) 852 – 258 = 594;
в) 963 – 369 = 594.
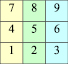
Рис. 14
Составим и исследуем аналогичные разности. Результат всегда равен 594 (в полученных разностях количество сотен и количество единиц отличается на 6, количество десятков одинаково, значит, разность равна 600 – 6 = 594).
Равенство разностей трёхзначных обращённых чисел, составленных из цифр, расположенных по горизонтальным линиям. Возьмем трехзначное число, составленное из цифр, расположенных по горизонтальной линии, например 987. Вычтем из 987 число, обращенное ему – 789 (рис.15). Получим 198. В аналогичных разностях результат всегда равен 198, т.к. количество сотен и количество единиц отличается 2, количество десятков одинаково, значит, разность равна 200 – 2 = 198.
а) 987 – 789 = 198;
б) 654 – 456 = 198;
в) 321 – 123 = 198.
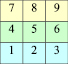
Рис. 15
Делимость суммы обращённых двузначных чисел, составленных из цифр, расположенных по вертикальным линиям на 11. Возьмем двузначное число, составленное из цифр, расположенных по вертикальной линии, например 74. Сложим его с обращенным числом – 47 (рис. 16). Получим 121. Составив аналогичные суммы и исследуя их, мы заметили: результат каждой суммы делится на 11 (складываются два числа десятков и те же два числа единиц, 10 + 1 = 11: в сумме число десятков равно числу единиц).
а) 74 + 47 = 121;
б) 85 + 58 =143;
в) 41 + 14 =55;
г) 52 + 25 = 77;
д) 63 + 36 = 99.
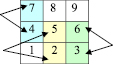
Рис. 16
Делимость суммы обращённых двузначных чисел, составленных из цифр, расположенных по горизонтальным линиям на 11. Рассмотрим аналогичные суммы чисел по горизонтальным линиям (рис.17):
а) 98 + 89 = 187;
б) 87 + 78 = 165;
в) 65 + 56 = 121;
г) 54 + 45 =99;
д) 32 + 23 =55…
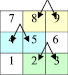
Рис. 17
Результат каждой суммы, также как и на вертикальных линиях делится на 11 (Вывод аналогичен).
Равенство суммы цифр разности обращённых двузначных чисел девяти. Можно заметить закономерность, связанную с вычислениями в п.1.5, 1.6, однако, это не сразу бросается в глаза. Вычислялась разность обращенных двузначных чисел. В результате вычислений получены числа: 9, 18, 27, 54 – у всех сумма цифр равна 9. Анализ результата исследования разности любых обращенных двузначных чисел (например: 84–48=36, 94–49=45, 92–29=63 и т.д.) показывает, что сумма цифр разности обращенных двузначных чисел всегда равна 9.
Закономерности, не зависящие от расположения чисел на клавиатуре микрокалькулятора
Умножение на 9. Так, как число 9 на единицу меньше 10 (10 – основание нашей (десятичной) системы счисления) обнаруживается еще одна удивительная закономерность, связанная с этим числом – можно сказать прием быстрого умножения: чтобы умножить какое-нибудь число на 9, нужно увеличить его в 10 раз и от полученного результата отнять само данное число. Умножим, например, 87 на 9. Нужно выполнить следующие действия: 87х10=870. Остается вычесть из 870 87, получим 783. Значит, 87х9=783.
Исследуя произведения различных чисел на 9, замечена интересная закономерность:
9х9=81
99х99=9801
999х999=998001
9999х9999=99980001
……………………….
Получение этой закономерности объясняется следующим образом:
9х(10–1)=90–9=81
99х(100–1)=9900–99=9801
999х(1000–1)=999000–999=998001
………………………………………
Нахождение наибольшего произведения чисел, составленных из набора цифр от 1 до 9 по одному разу. Возникает вопрос: какое наибольшее произведение может получиться, если нажать по одному разу каждую из клавиш

Один из способов ответить на этот вопрос – перебрать все возможные варианты.
Исследования с наименьшим набором клавиш с цифрами 1, 2, 3 (Приложение 3) показали, что произведение 3х21 является наибольшим.
Аналогичные исследования с набором клавиш с цифрами 1, 2, 3, 4 (Приложение 4) позволяют сделать вывод, что наибольшим произведением является произведение 41 на 32.
Чтобы произведение было наибольшим, нужно, конечно, перемножить наибольшие числа, составленные из предложенного набора цифр. Число будет наибольшим, если в высшем разряде стоит цифра, порядок которой выше остальных. Потом – порядок, которой также выше остальных и т.д. Из перебора вариантов нами исключены произведения чисел однозначных на трехзначные, т.к. получаемые произведения всегда меньше произведений двухзначных чисел. Исходя из вышесказанного, исследования сводятся до минимума.
Исследования с набором клавиш с цифрами 1, 2, 3, 4, 5 (Приложение 5) показали, что произведение 431х52 является наибольшим, а для набора клавиш с цифрами от 1 д о 6 наибольшее произведение дают числа 631 и 542.
Наблюдения показывают (Приложения 6,7), что, если записать полученные числа в столбик, начиная с высшего разряда, можно нарисовать схему, по которой они составлены:
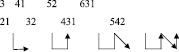
Анализ полученных произведений и схем позволяет выработать общий метод для нахождения наибольшего произведения для набора из всех ненулевых клавиш:
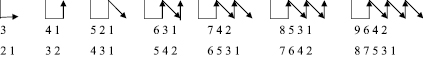
Таким образом, по предложенной схеме, можно для любого набора клавиш составить числа, произведение которых будет наибольшим.
В полученных числах мы увидели и другой способ их составления: зная числа наибольшего произведения из меньшего набора клавиш, например для клавиш от одного до 4 (41х32), можно легко составить числа для набора клавиш от 1 до 5: высший разряд меньшего числа (3), ставится на второе место в большее число (431), а добавляемая цифра (5) на место высшего разряда в меньшее число (52). Имеем произведение 431 на 52. Для большего набора клавиш действия аналогичные.
Библиографическая ссылка
Иниваткин Е.А. МИКРОКАЛЬКУЛЯТОР: ЗАКОНОМЕРНОСТИ ЧИСЕЛ, РАСПОЛОЖЕННЫХ НА КЛАВИАТУРЕ // Международный школьный научный вестник. 2017. № 3-3. ;URL: https://school-herald.ru/ru/article/view?id=358 (дата обращения: 12.03.2026).
