Данная статья является реферативным изложением основной работы. Полный текст научной работы, приложения, иллюстрации и иные дополнительные материалы доступны на сайте III Международного конкурса научно-исследовательских и творческих работ учащихся «Старт в науке» по ссылке: https://www.school-science.ru/0317/7/28974.
Когда мы переходим в следующий класс, предмет математики нам преподносит все новые сюрпризы, появляются совершенно непривычные термины, функции: корни, синусы, логарифмы, страшные на вид и на слух. Как тут не вспомнить о таблице умножения и дробях в начальных классах? Кажется, что это совершенно разные вещи, то, что мы учили тогда и то с чем надо разбираться сейчас, словом – это просто как небо и земля. А так ли это на самом деле? Было бы очень полезно увидеть какую-то связь, которая дает возможность видеть общее сложных функций, изучаемых старших классах, с методами математики начальных классов. Действительно, математика проста и сложна одновременно тем, что мостики существуют между, казалось бы, совершенно разными областями. Одним из таких мостиков являются цепные дроби. Одновременная их простота и многообразие удивляет. Все что надо, что бы «жонглировать» цепными дробями – это арифметические операции: сложение, умножение и т.д. Фантастика, не может быть! скажет любой старшеклассник. Но это правда и это еще не все. Цепные дроби – это способ построения интересных фигур – да, да – это еще и геометрия. Все вместе это складывается в единую систему. Овладев это системой, этим подходом можно оглянуться вокруг и увидеть цепные дроби в предметах окружающего мира, которые на первый взгляд никак не связаны с математикой.
В настоящей работе были поставлены следующие цели:
1. Изучение способа записи цепных дробей.
2. Применение цепных дробей для приближенного вычисления значений корней и специальных функций.
3. Исследование геометрических свойств цепных дробей.
4. Для достижения поставленных целей мне необходимо решить следующие задачи:
5. Познакомиться с понятием цепных дробей и их классификации.
6. Освоить математические методы компактной записи цепных конечных и непрерывных дробей.
7. Получить формулы цепных дробей для практических расчетов.
8. Освоить геометрическую форму представления цепных дробей.
9. Найти геометрическое подобие цепных дробей в объектах окружающего мира.
Актуальность данной темы состоит в том, что она интересна своим применением в разнообразных задачах, в том числе и задачах олимпиадного характера, которые встречаются на экзаменах. Действительные числа однозначно отображаются цепными дробями. Основное значение такого изображения заключается в том, что, зная цепную дробь, изображающую действительное число, можно определить это число с достаточной точностью. Новизна моей работы состоит в попытке предложить свои алгебраические выражения для цепных дробей и связать их геометрическими построениями. Сформулируем рабочую гипотезу в виде предположения о том, что алгебраические выражения и геометрические объекты, соответствующие цепным дробям, повсеместно встречаются в окружающем мире. Я думаю, что это было бы очень полезно установить на практических примерах.
Моя работа состоит из Введения, трех глав, Практической части, Выводов, Заключения и Списка литературы.
Понятие о цепных дробях и их классификация
Теория цепных дробей – это одна из древнейших математических теорий. Цепные дроби были введены в 1572 году итальянским математиком Бомбелли. Современное обозначение непрерывных дробей встречается у итальянского математика Катальди в 1613 году. Величайший математик XVIII века Леонард Эйлер первый изложил теорию цепных дробей. Работы Эйлера по теории цепных дробей были продолжены М. Софроновым (1729–1760), академиком В.М. Висковатым (1779–1819), Д. Бернулли (1700–1782) и др. Многие принципиальные результаты данной теории принадлежат французскому математику Лагранжу. К мысли о цепной дроби математики пришли при рассмотрении практического вопроса: какой самый естественный способ приближённого представления положительных чисел дробями? [1]
Чтобы показать, что такое цепная дробь, начнём с простого примера. Возьмём дробь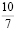 
. Наибольшее целое число, не превосходящее эту дробь – это 1:
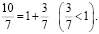
«Перевернем» дробь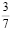 
:
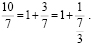
Наибольшее целое число не превосходящее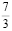 
– это 2. Получаем:
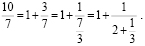
Это и есть окончательное представление дроби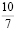 
в виде цепной дроби
,
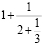потому что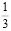 
в конце цепочки после «переворота» будет уже целым числом.
Перейдем к произвольному рациональному числу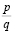 
. Проведя процедуру описанную выше необходимое число раз, получим конечную цепную дробь
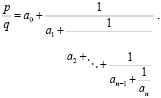
Числа, входящие в цепную дробь, называются неполными частными, из них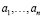 
– натуральные, а 
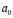– целое. Цепную дробь удобно записывать в компактной форме 
.
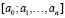Иррациональные числа разлагаются в бесконечные цепные дроби. Число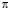 
является одним из самых известных иррациональных чисел. Оно представляется в виде бесконечной цепной дроби и может быть представлено только лишь с указанием начальных неполных частных
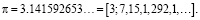
Обрывая цепную дробь, можно получать очень хорошие рациональные приближения к данному числу, которые называются подходящими дробями (нумерация подходящих дробей, как и неполных частных, начинается с нуля). C древних времен для числа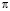 
известны приближения
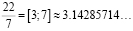
и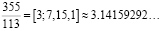 
Первая подходящая дробь отличается от точного значения во второй цифре после запятой, а в третьей подходящей дроби ошибка появляется в седьмой цифре после запятой (неверные цифры закрашены серым).
Существуют иррациональные числа, у которых бесконечные цепные дроби содержат периодически повторяющиеся неполные частные. Такие цепные дроби называются периодическими цепными дробями. Например,
,
.
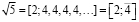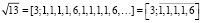Здесь период отмечается чертой. Периодические цепные дроби соответствуют числам с квадратичной иррациональностью, т.е. числам являющихся корнями квадратных уравнений с целыми коэффициентами. Поэтому периодические цепные дроби представляются особый интерес для изучения в школе.
Оценка погрешности при замене действительного числа его подходящей дробью выполняется с использованием теоремы. Для любых двух соседних подходящих дробей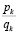 
и 
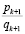к действительному числу 
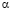имеет место неравенство
,
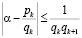и если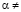 
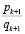, то
.
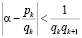Цепные дроби дают очень удобный аппарат для решения задач такого рода. С помощью цепных дробей удается заменять действительные числа рациональными дробями так, что ошибка от такой замены мала по сравнению со знаменателями этих рациональных чисел [2].
Геометрия цепных дробей
В основе геометрии чисел по Минковскому лежит школьная тетрадка в клеточкуплоскость, на которой нарисована координатная сетка [3]. Рассмотрим прямую y=ax; возьмём для примера a=10/7. Если a – рациональное число, то на этой прямой, кроме начала координат, будут ещё целые точки. В нашем случае прямая пройдёт через точку (7, 10).
Оказывается, построение цепной дроби числа a связано с нахождением целых точек, которые лежат близко от нашей прямой. А именно, имеется геометрический алгоритм, который предложил крупнейший российский математик Борис Николаевич Делоне. Он выразительно называл этот алгоритм «вытягиванием носов». Алгоритм позволяет строить ближайшие к прямой целые точки одну за другой и одновременно получать цепную дробь.
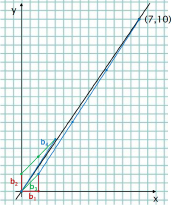
Рис. 1. Алгоритм «вытягивания носов»
Пусть b1 – горизонтальный отрезок единичной длины, а b2 – горизонтальный. Между ними расположена наша прямая (рис. 1). Теперь к концу отрезка b1 будем приставлять отрезки b2 до тех пор, пока не перескочим через нашу прямую. Другими словами, нужно найти наибольшее натуральное число a0 такое, что конец получившейся ломаной, состоящей из b1 и a0 раз b2, всё ещё ниже нашей прямой. В данном случае помещается только один отрезок, т.е. a0=1. Если соединить начало b1 и конец ломаной, то получится новый отрезок b3. Продолжаем процедуру. Теперь мы будем приставлять отрезок b3 в конец отрезка b2. Аналогично, на выбираем a2 (число отрезков b3) так, чтобы не перескочить через прямую, т. е. чтобы конец ломаной оставался выше прямой, а если к нему прибавить еще один b3, то мы перескочим через прямую. Как видим, a1=2. Если теперь соединить начало b2 и конец ломаной получим отрезок b4. Отрезки получаются всё более длинные, поэтому алгоритм и назвали «вытягиванием носов».
Далее, если взять три отрезка b4 (т.е. a2=3) и добавить в конец b3, попадаем как раз на прямую. Итак получили, a0=1, a1=2, a2=3,
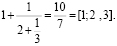
Можно доказать, что этот алгоритм всегда даёт целые числа a0, a1, a2, … , которые и будут получаться при разложении a в цепную дробь. Точки, которые мы получаем, дают нам сразу же и элементы цепной дроби.
Цепные дроби вокруг нас
В этой главе мы рассмотрим ряд примеров раскрывающие использование цепных дробей в различных областях окружающего мира [4].
Если, разорвав прямоугольный лит бумаги пополам, мы хотим получить два новых листа с тем же отношение сторон, то стороны исходного листа должны относится друг к другу как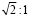 
. Действительно, если мы разорвем пополам прямоугольник со сторонами 
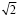и 1, то каждая половинка будет иметь длинную сторону 1, а короткую
.
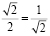Отношение этих сторон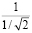 
опять равно 
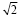. Именно таким свойством обладают форматы бумаги серии A (А0, А1, …). Я в этом убедилась разорвав лист формата А4 (см. рис 2).
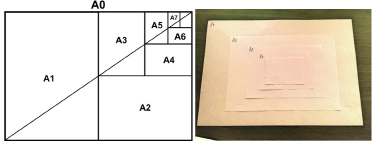
Рис. 2. Рвём А4
Размер стандартного хорошо нам известного листа бумаги А4 – 210*297 мм. Отношение сторон этого листа
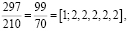
а это пятая подходящая дробь к числу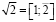 
. Погрешность такого приближения невелика
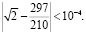
Любопытно, что произведение сторон листа в метрах мало отличается от 1/24=1/16:
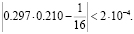
Это связано с тем, что лист А4 составляет 1/16 от листа ватмана А0, площадь которого равна 1 м2. Я нашла цепные дроби всех форматов и обнаружила, что А4 имеет самое лучшее приближение. К примеру, А0 (841*1189 мм) – это только четвертая подходящая дробь числа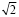 
.
Голландский ученый Христиан Гюйгенс в 1862 году построил один из первых механических планетариев. Теорию цепных дробей он применил при проектировании зубчатых колес, что обеспечило высокую точность во взаимном движении моделей планет. Старинные часы известных мастеров также содержали шестеренки, отношение зубцов рассчитывалось по законам цепных дробей [5].
Наверно все слышали, что стандартное электрическое напряжение в наших розетках 220 Вольт. Если кто-то обращал внимание на надписи на импортных электрических приборах, то они рассчитаны так же и на меньшее напряжение. Например, в странах Северной Америки стандартом сетевого напряжения составляет 127 Вольт. Наверно все видели надписи на столбах или трансформаторных будках «380 В». Почему именно эти значения? Оказывается это объясняется трехфазным устройством электрических сетей. Отношения
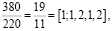
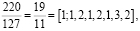
это хорошие приближения к числу
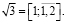
Как известно 1 год=365 суток 5 часов 48 минут 46 секунд, что можно выразить десятичной дробью 365.242199…суток. Подходящие дроби к длине солнечного года, измеренного в солнечных сутках
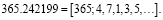
Такое представление позволяют строить солнечные календари. Первая подходящая дробь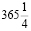 
соответствует юлианскому стилю (назван по имени Юлия Цезаря), в котором каждый четвертый год високосный. Вычислим разницу 
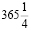– 365.242199 = =0.007801 сут = 0.187224 час = 11.23344 мин = 11 мин 14 сек, то есть средняя длина года больше настоящей на 11 мин 14 сек.
Третья подходящая дробь
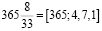
лежала в основе персидского (иранского) календаря, который в 1079 году предложил математик, астроном и поэт Омар Хайям. В таком календаре все годы разбиваются на 33–летние циклы, внутри цикла семь раз високосным является каждый четвертый год, а на восьмой раз – пятый. Схематически его можно изобразить так: IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII (палочками обозначены года, а високосные перечеркнуты). Разность продолжительности такого календарного года с астрономическим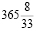 
– –365.242199 = 0.000225242 сут = =0.005406 час = 0.324348 мин = 19.5 сек, то есть ошибка всего 19 сек в год, но использование такого календаря оказалось неудобным [6].
Четвертое приближение <<st48.wmf>> дает еще один календарь, предложенный русским астрономом Иоганном Генрихом Медлером в 1864 году. Медлер предложил ввести этот календарь в России с XX столетия. Для этого необходимо было каждые 128 лет пропускать 1 високосный, так как по юлианскому календарю приходилось 32 високосных на 128 лет. Но этот календарь не был принят, так как видимо 128 число не круглое. Вычислим ошибку.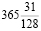 
– –365.242199 = -0.0000115 сут = -0.000276 час = -0,01656 мин = -0.99 сек –1 сек! Предложение Медлера так и не было принято.
В 1582 году папа Григорий XIII исправил неточность юлианского календаря и произвел реформу. Так же оставалось чередование простых и високосных лет, но, если номер оканчивался двумя нулями, а число сотен не делилось на 4, то этот год был простой. Например 1500 год простой, а 1600 високосный. Ну и начиная с рождества Христова накопилась ошибка в 10 дней, с тех пор накопилась еще ошибка в 3 дня (1700, 1800,1900 годы). Итак расхождение сейчас с юлианским календарем составляет в 13 дней. Выясним длину григорианского года. Из 400 лет по юлианскому календарю 100 високосных, а по григорианскому – 97, поэтому средняя длина григорианского года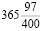 
суток=365.2425 суток=365 суток 5 часов 49 мин 12 сек, т. е. она больше истиной на 26 сек. Получилось намного хуже календаря Медлера, что не удивительно, ведь 
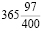не является подходящей дробью.
Библиографическая ссылка
Степанова А.Р. ЦЕПНЫЕ ДРОБИ В ОКРУЖАЮЩЕМ МИРЕ // Международный школьный научный вестник. – 2017. – № 3-3. ;URL: https://school-herald.ru/ru/article/view?id=360 (дата обращения: 18.04.2024).