Данная статья является реферативным изложением основной работы. Полный текст научной работы, приложения, иллюстрации и иные дополнительные материалы доступны на сайте III Международного конкурса научно-исследовательских и творческих работ учащихся «Старт в науке» по ссылке: https://www.school-science.Ru/0317/7/29153
Решение алгебраических уравнений высших степеней с одним неизвестным представляет собой одну из труднейших и древнейших математических задач. Этими задачами занимались самые выдающиеся математики древности.
Решение уравнений n-ой степени является важной задачей и для современной математики. Интерес к ним достаточно велик, так как эти уравнения тесно связаны с поиском корней уравнений, не рассматриваемых школьной программой по математике.
Проблема: отсутствие навыков решения уравнений высших степеней различными способами у учащихся мешает им успешно подготовиться к итоговой аттестации по математике и математическим олимпиадам, обучению в профильном математическом классе.
Перечисленные факты определили актуальность нашей работы «Решение уравнений высших степеней».
Владение простейшими способами решения уравнений n-ой степени сокращает время для выполнения задания, от которого зависит результат работы и качество процесса обучения.
Цель работы: изучение известных способов решения уравнений высших степеней и выявление наиболее доступных из них для практического применения.
Исходя из поставленной цели, в работе определены следующие задачи:
– изучить литературу и Интернет-ресурсы по данной теме;
– познакомиться с историческими фактами, касающимися данной темы;
– описать различные способы решения уравнений высших степеней;
– сравнить степень сложности каждого из них;
– познакомить одноклассников со способами решения уравнений высших степеней;
– создать подборку уравнений для практического применения каждого из рассмотренных способов.
Объект исследования – уравнения высших степеней с одной переменной.
Предмет исследования – способы решения уравнений высших степеней.
Гипотеза: общего способа и единого алгоритма, позволяющего за конечное число шагов находить решения уравнений n-ой степени, не существует.
Методы исследования:
– библиографический метод (анализ литературы по теме исследования);
– метод классификации;
– метод качественного анализа.
Теоретическая значимость исследования состоит в систематизации способов решения уравнений высших степеней и описании их алгоритмов.
Практическая значимость – предъявленный материал по данной теме и разработка учебного пособия для учащихся по данной теме.
1. УРАВНЕНИЯ ВЫСШИХ СТЕПЕНЕЙ
1.1 Понятие уравнения n-ой степени
Определение 1. Уравнением n-ой степени называется уравнение вида
a0xⁿ+a1xn‑1+a2xⁿ-²+…+an‑1x+an = 0, где коэффициенты a0, a1, a2…, an-1, an – любые действительные числа, причем, a0 ≠ 0 [3].
Многочлен a0xⁿ+a1xn‑1+a2 xⁿ-²+…+an‑1x+an называют многочленом n-ой степени. Коэффициенты различают по названиям: a0 – старший коэффициент; an – свободный член.
Определение 2. Решениями или корнями для данного уравнения являются все значения переменной х, которые обращают это уравнение в верное числовое равенство или, при котором многочлен a0 xⁿ+a1 xn‑1+a2xⁿ-²+…+an‑1x+an обращается в нуль. Такое значение переменной х называют также корнем многочлена. Решить уравнение – это значит найти все его корни или установить, что их нет.
Если a0 = 1, то такое уравнение называют приведенным целым рациональным уравнением n-й степени.
Для уравнений третьей и четвертой степени существуют формулы Кардано и Феррари, выражающими корни этих уравнений через радикалы. Выяснилось, что на практике ими редко пользуются. Таким образом, если n ≥ 3, а коэффициенты многочлена произвольные действительные числа, то поиск корней уравнения – задача непростая. Тем не менее, во многих частных случаях эта задача решается до конца. Остановимся на некоторых из них.
1.2 Исторические факты решения уравнений высших степеней
Уже в древности люди осознали, как важно научиться решать алгебраические уравнения. Около 4000 лет назад вавилонские ученые владели решением квадратного уравнения и решали системы двух уравнений, из которых одно – второй степени. С помощью уравнений высших степеней решались разнообразные задачи землемерия, архитектуры и военного дела, к ним сводились многие и разнообразные вопросы практики и естествознания, так как точный язык математики позволяет просто выразить факты и соотношения, которые, будучи изложенными обычным языком, могут показаться запутанными и сложными.
Универсальной формулы для нахождения корней алгебраического уравнения n-ой степени нет. Многим, разумеется, приходила в голову заманчивая мысль найти для любой степени n формулы, которые выражали бы корни уравнения через его коэффициенты, то есть, решали бы уравнение в радикалах.
Только в 16 веке итальянским математикам удалось продвинуться дальше – найти формулы для n = 3 и n = 4. Одновременно вопросом об общем решении уравнений 3-й степени занимались Сципион, Даль, Ферро и его ученики Фиори и Тарталья.
В 1545 году вышла книга итальянского математика Д. Кардано «Великое искусство, или о правилах алгебры», где наряду с другими вопросами алгебры рассматриваются общие способы решения кубических уравнений, а также метод решения уравнений 4-й степени, открытый его учеником Л. Феррари [12].
Полное изложение вопросов, связанных с решением уравнений 3-й и 4-й степеней, дал Ф. Виет.
В 20-х годах 19 века, норвежский математик Н. Абель доказал, что корни уравнений пятой степени не могут быть выражены через радикалы [5,42].
В ходе исследования было выявлено, что современной науке известно множество способов решения уравнений n-ой степени.
Результатом поиска методов решения уравнений высших степеней, неподдающихся решению способами, рассматриваемыми в школьной программе, стали способы, основанные на применении теоремы Виета (для уравнений степени n>2), теоремы Безу, схемы Горнера, а также формула Кардано и Феррари для решения кубических уравнений и уравнений четвертой степени.
В работе представлены методы решения уравнений и их виды, которые для нас стали открытием. К ним можно отнести – метод неопределенных коэффициентов, выделение полной степени, симметрические уравнения.
2. РЕШЕНИЕ ЦЕЛЫХ УРАВНЕНИЙ ВЫСШИХ СТЕПЕНЕЙ С ЦЕЛЫМИ КОЭФФИЦИЕНТАМИ
2.1 Решение уравнений 3-ей степени. Формула Д. Кардано
Рассмотрим уравнения вида x3+px+q=0. Преобразуем уравнение общего вида к виду: x3+px2+qx+r=0. Запишем формулу куба суммы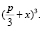 
Сложим с первоначальным равенством и заменим 
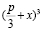на y. Получим уравнение: 
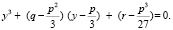После преобразований, имеем: y2+py + q=0. Теперь, снова запишем формулу куба суммы:
(a + b)3=a3 + 3a2b + 3ab2 + b3= a3 + b 3+ 3ab (a + b), заменим (a + b) на x, получим уравнение x3–3abx – (a3+b3) = 0. Теперь видно, что исходное уравнение равносильно системе: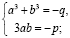 
и 
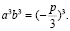Решая систему, получим:
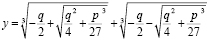
Мы получили формулу для решения приведенного уравнения 3-й степени. Она носит имя итальянского математика Кардано.
Рассмотрим пример. Решить уравнение:
.
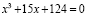Имеем р = 15 и q = 124, тогда используя формулу Кардано вычислим корень уравнения.
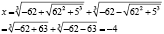
Вывод: данная формула хороша, но не подходит для решения всех кубических уравнений. Вместе с тем она громоздка. Поэтому на практике ею пользуются редко.
Но тот, кто овладеет данной формулой, может использовать ее при решении уравнений третьей степени на ЕГЭ.
2.2 Теорема Виета
Из курса математики мы знаем данную теорему для квадратного уравнения, но мало кто знает, что ее используют и для решения уравнений высших степеней.
Рассмотрим уравнение:
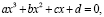разложим левую часть уравнения на множители 
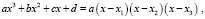разделим на 
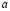= 0.
;
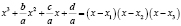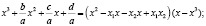
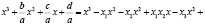
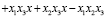. Правую часть уравнения преобразуем к виду
;
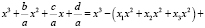
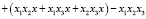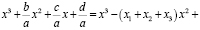
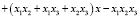; отсюда следует, можно записать в систему следующие равенства:
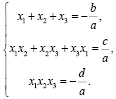
Формулы, выведенные Виетом для квадратных уравнений и продемонстрированные нами для уравнений 3-й степени, верны и для многочленов высших степеней.
Решим кубическое уравнение:
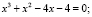
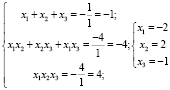
Вывод: данный способ универсален и достаточно легок для понимания учащимися, так как теорема Виета им знакома по школьной программе для n = 2. Вместе с тем, чтобы находить корни уравнений с помощью данной теоремы необходимо обладать хорошими вычислительными навыками.
2.3 Теорема Безу
Эта теорема, названа по имени французского математика XVIII века Ж. Безу.
Теорема. Если уравнение a0xⁿ+a1xn‑1+a2xⁿ-²+…+an‑1x+an = 0, в котором все коэффициенты целые числа, причем свободный член отличен от нуля, имеет целый корень, то этот корень является делителем свободного члена.
Учитывая, что в левой части уравнения многочлен n-й степени, то теорема имеет и другую трактовку.
Теорема. При делении многочлена n-й степени относительно x на двучлен x – a остаток равен значению делимого при x = a. (буква a может обозначать любое действительное или мнимое число, т. е. любое комплексное число) [5,47].
Доказательство: пусть f(x) обозначает собой произвольный многочлен n-й степени относительно переменной x и пусть при его делении на двучлен (x – a) получилось в частном q(x), а в остатке R. Очевидно, что q(x) будет некоторый многочлен (n–1)-й степени относительно x, а остаток R будет величиной постоянной, т. е. не зависящей от x.
Если бы остаток R был многочленом первой степени относительно x, то это означало бы, что деление не выполнено. Итак, R от x не зависит. По определению деления получаем тождество: f(x) =(x–a) q(x)+R.
Равенство справедливо при всяком значении x, значит, оно справедливо и при x=a, получим: f(a)=(a–a) q(a)+R. Символ f(a) обозначает собой значение многочлена f(x) при x=a, q(a) обозначает значение q(x) при x=a. Остаток R остался таким, каким он был раньше, так как R от x не зависит. Произведение (x–a) q(a) = 0, так как множитель (x–a) = 0, а множитель q(a) есть определенное число. Поэтому из равенства получим: f(a)= R, ч. т. д.
Пример 1. Найти остаток от деления многочлена x3–3x2+6x-5 на двучлен x-2. По теореме Безу: R=f (2) =23–3•22 + 6•2–5=3. Ответ: R=3.
Отметим, что теорема Безу важна не столь сама по себе, сколько своими следствиями. (Приложение 1)
Остановимся на рассмотрении некоторых приемов применения теоремы Безу к решению практических задач. Следует отметить, что при решении уравнений с помощью теоремы Безу необходимо:
– найти все целые делители свободного члена;
– из этих делителей найти хотя бы один корень уравнения;
– левую часть уравнения разделить на (х–а);
– записать в левой части уравнения произведение делителя и частного;
– решить полученное уравнение.
Рассмотрим на примере решения уравнения х3 + 4х2 + х – 6 = 0.
Решение: находим делители свободного члена ±1; ± 2; ± 3; ± 6. Вычислим значения при х=1, 13 + 4•12 + 1–6=0. Разделим левую часть уравнения на (х-1). Деление выполним «уголком», получим:
|
х3 + 4х2 + х – 6 x-1 x3 – x2 x2+5x +6 5x2 + x – 6 5x2–5x 6x – 6 6x – 6 0 |
Таким образом левую часть уравнения можно представить в виде произведения двух множителей и решить его (х – 1)(х2 + 5х + 6) = 0, получим корни уравнения: х = – 3; – 2; 1. |
Вывод: теорема Безу один из тех способов, которые мы рассматриваем в нашей работе, изучается в программе факультативных занятий. Она трудна в понимании, потому что, чтобы ей владеть, надо знать все следствия из нее, но при этом теорема Безу является одним из главных помощников учащихся на ЕГЭ.
2.4 Схема Горнера
Для деления многочлена на двучлен х–- можно использовать специальный несложный прием, придуманный английскими математиками XVII века, впоследствии названной схемой Горнера. Помимо нахождения корней уравнений, по схеме Горнера можно более просто вычислять их значения. Для этого необходимо подставить значение переменной в многочлен Pn(x)=a0 xn+a1 xn‑1+a2 xⁿ-²+…++ an‑1 x+an. (1).
Рассмотрим деление многочлена (1) на двучлен x–-.
Выразим коэффициенты неполного частного b0xⁿ-¹+b1xⁿ-²+b2xⁿ-³+…+bn‑1 и остаток R через коэффициенты многочлена Pn(x) и число α. b0=a0,b1= αb0+a1, b2= αb1+a2…, bn‑1= = αbn‑2+an‑1 = αbn‑1+an.
Вычисления по схеме Горнера представлены в виде следующей таблицы:
|
а0 |
a1 |
a2, |
… |
an |
|
|
α |
b0=а0 |
b1= αb0+a1 |
b2= αb1+a2 |
… |
r=αbn-1+an |
Поскольку R=Pn(α), то α – корень уравнения. Для того чтобы проверить не является ли α кратным корнем, схему Горнера можно применить уже к частному b0x+b1x+…+bn-1 по таблице. Если в столбце под bn-1 получится снова 0, значит α – кратный корень.
Рассмотрим пример: решить уравнение х3 + 4х2 + х – 6 = 0.
Применим к левой части уравнения разложение на множители многочлена, стоящего в левой части уравнения, схему Горнера.
Решение: находим делители свободного члена ±1; ± 2; ± 3; ± 6.
|
1 |
4 |
1 |
-6 |
|
|
1 |
1 |
1 • 1 + 4= 5 |
5 • 1 + +1= 6 |
6 • 1 + +(–6) = 0 |
Коэффициенты частного – числа 1, 5, 6, а остаток R = 0.
Значит, х3 + 4х2 + х – 6 = (х – 1) (х2 + 5х + + 6) = 0.
Отсюда: х – 1 = 0 или х2 + 5х + 6 = 0.
х = 1, х1 = –2; х2 = –3. Ответ: 1, –2, –3.
Вывод: таким образом, на одном уравнении мы показали применение двух различных способов разложения на множители многочленов. На наш взгляд, схема Горнера наиболее практична и экономична.
2.5 Решение уравнений 4-й степени. Метод Феррари
Ученик Кардано Людовик Феррари обнаружил способ решения уравнения 4-й степени. Метод Феррари состоит из двух этапов.
I этап: уравнение вида
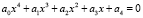
представляется в виде произведения двух квадратных трехчленов – это следует из того, что уравнение 3-й степени и хотя бы одно решение.
II этап: полученные уравнения решаются при помощи разложения на множители, однако для того, чтобы найти требуемое разложение на множители, приходится решать кубические уравнения.
Идея в том, чтобы представить уравнения в виде A2=B2, где A=x2+s,
B-линейная функция от x. Тогда остается решить уравнения A = ±B.
Для наглядности рассмотрим уравнение:
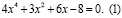
Уединим 4-ю степень, получим:
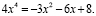
Для любого d выражение
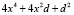
будет полным квадратом. Прибавим к обеим частям уравнения
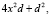
получим
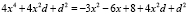(2)
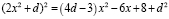(3)
В левой части полный квадрат, можно подобрать d, чтобы и правая часть (2) стала полным квадратом. Представим себе, что мы достигли этого. Тогда наше уравнение выглядит так:
.
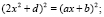
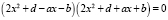Найти корень впоследствии не составит никакого труда. Чтобы правильно подобрать d надо, чтобы дискриминант правой части (3) обратился в нуль, т. е.
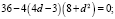
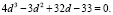
Итак, чтобы найти d, надо решить это уравнение 3-й степени. Такое вспомогательное уравнение называют резольвентой [11].
Легко находим целый корень резольвенты: d = 1
Подставив в (1) уравнение получим
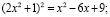
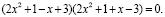
Далее решаем каждое уравнение. Найдем корни (1) уравнения. В данном случае, это
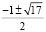
Вывод: метод Феррари универсален, но сложен и громоздкий. Вместе с тем, если алгоритм решения понятен, то уравнения 4-й степени можно решать данным методом.
2.6 Метод неопределенных коэффициентов
Успех решения уравнения 4-й степени методом Феррари зависит от того, реши ли мы резольвенту – уравнение 3-й степени, что как мы знаем, не всегда удается.
Суть метода неопределенных коэффициентов состоит в том, что вид сомножителей, на которые разлагается данный многочлен, угадывается, а коэффициенты этих сомножителей (также многочленов) определяется путем перемножения сомножителей и приравнивания коэффициентов при одинаковых степенях переменной [8,9].
Пример: решите уравнение:
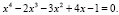
Предположим, что левую часть нашего уравнения можно разложить на два квадратных трехчлена с целыми коэффициентами такие, что справедливо тождественное равенство
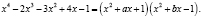
Очевидно, что коэффициенты перед x2 у них должны быть равными 1, а свободные члены – у одного +1, у другого – 1.
Неопределенными остаются коэффициенты, стоящие перед х. Обозначим их через а и b и чтобы их определить, перемножим оба трехчлена правой части уравнения.
В результате получим:
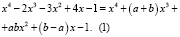
Приравнивая коэффициенты при одинаковых степенях х в левой и правой частях равенства (1), получаем систему для нахождения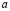 
и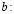 
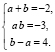
Решив эту систему, будем иметь:
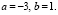
Итак, наше уравнение равносильно уравнению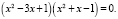 
Решив его, получаем следующие корни:
.
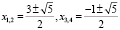Метод неопределенных коэффициентов опирается на следующие утверждения: любой многочлен четвертой степени, стоящий в уравнении, можно разложить на произведение двух многочленов второй степени; два многочлена тождественно равны тогда и только тогда, когда равны их коэффициенты при одинаковых степенях х.
2.7 Симметрические уравнения
Определение. Уравнение вида
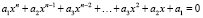называется симметрическим, если первые коэффициенты, стоящие в уравнении слева, равны первым коэффициентам, стоящим справа [8,15].
Мы видим, что первые коэффициенты слева равны первым коэффициентам справа.
Если такое уравнение имеет нечетную степень, то оно имеет корень х = –1. Далее мы можем понизить степень уравнения, поделив его на (х+1). Оказывается, что при делении симметрического уравнения на (х+1) получается симметрическое уравнение четной степени. Доказательство симметричности коэффициентов представлено ниже. (Приложение 6) Наша задача – научиться решать симметрические уравнения четной степени.
Например:
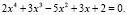(1)
Решим уравнение (1), поделим на х2 (на среднюю степень):
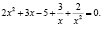
Сгруппируем слагаемые с симметричными коэффициентами, которые вынесем за скобки:
.
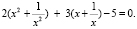Обозначим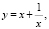 
возведем обе части в квадрат, отсюда
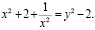
Итак,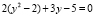 
или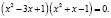 
решив уравнение, получим 
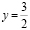, у = –3.
Далее вернемся к замене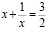 
и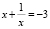 
.
Получим уравнения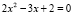 
и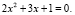 
Первое не имеет решения, а второе имеет два корня.
Ответ:
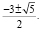
Вывод: данный вид уравнений не часто встречающийся, но если он вам попался, то его можно решить легко и просто не прибегая к громоздким вычислениям.
Библиографическая ссылка
Габов Н. А. УРАВНЕНИЯ ВЫСШИХ СТЕПЕНЕЙ С ОДНОЙ ПЕРЕМЕННОЙ // Международный школьный научный вестник. – 2017. – № 5-1. ;URL: https://school-herald.ru/ru/article/view?id=399 (дата обращения: 16.04.2024).