Международный школьный научный вестник

Научный журнал для старшеклассников и учителей ISSN 2542-0372

• Авторы
• Научный руководитель
• Файлы
• Литература

Черных К.Д.  1

---

1 с. Кинель-Черкассы Самарской области, ГБОУ СОШ №1 «ОЦ», 9 класс

Зимовец Т.И. (с. Кинель-Черкассы Самарской области, ГБОУ СОШ №1 «ОЦ»)

Статья в формате PDF

0 KB

1. Агрохимия / Под. ред. Г.Б. Ягодина. 2-е изд., перераб. и доп. – М.: Агропромиздат, 1989. – 654 с.

2. Зейдис И.М., Кружалин В.И., Симонов Ю.Г. и др. Общие свойства динамики гeocиcтем // Вестник МГУ. – 2001. – Сер. 5 – №4. – С. 3 – 9.

3. Клиническая оценка лабораторных тестов: Пер. с англ. / Под ред. Н.Т. Тица. – М.: Медицина, 1986. – 480 с.

4. Лапко А.В. Статистические методы моделирования и принятия решений в развивающихся медико-биологических системах. /А.В. Лапко, О.М. Новиков, Л.С. Поликарпов; Отв. ред. К.Р. Седов, А.М. Федотов; АН СССР, Сиб. отделение, Краснояр. науч.центр, ВЦ. – Новосибирск: Наука, Сибирское отд-ние, 1991. – 216 с.

5. Лядов В.Р. Основы теории вероятностей и математической статистики: для студентов мед. ВУЗов. – СПб.: Фонд «Инициатива», 1998. – 107 с.

6. Матвеев Н.М., Павловский В.А., Прохорова Н.В. Экологические основы аккумуляции, тяжёлых металлов сельскохозяйственными растениями в лесостепном и степном Поволжье. – Самара: Изд-во Сам. ун-т, 1997. – 215 с.

7. Урбах В.Ю. Статистический анализ в биологических и медицинских исследованиях. – М.: Медицина, 1975. – 295 с.

8. Ферстер Э., Рёнц Б. Методы корреляционного и регрессионного анализа: Руководство для экономистов / Пер. с нем. – М.: Финансы и статистика, 1983. – 302 с.

9. Шиманчик И.П. Некоторые аспекты моделирования медико-географической ситуации как случайного процесса // Шестое Сибирское совещание по климато-экологическому мониторингу. Материалы совещания. – Томск,2005. – С.447–450.

10. Юнкеров В.И., Григорьев С.Г. Математико-статистическая обработка данных медицинских исследований. – СПб.: ВМедА, 2002. – 266 с.

На современном этапе развития научных исследований становится явно недостаточно провести простое описание изучаемого явления. Обязательным требованием является такая форма результата, которая может быть применена на практике в виде математической модели, программного продукта и т.п. Учитывая это, в качестве основного метода исследования были выбраны математические методы.

В настоящей работе приводятся методы математической статистики и корреляционно-регрессионный анализ, примененные для анализа экологических опытов.

Прежде чем выполнять математические расчёты в любой системе, необходимо отметить, что математический анализ отличается объективностью и динамичностью.

В настоящее время становится всё более закономерным увеличение доли математических методов в современных исследованиях, именно поэтому тема исследования актуальна.

Целью работы является обоснование применения основных математических методов в экологических исследованиях.

Реализация цели осуществляется через ряд задач:

• изучить литературные источники по теме исследований;

• собрать статистический материал, провести опыты и наблюдения;

• обработать данные и написать научную работу.

В работе обобщены и систематизированы данные, полученные из фондовых источников Кинель- Черкасского района, НИИ «ВолгоГипрозема», и собственных наблюдениях, выполненных на базе школьного научного общества.

Статистическая обработка данных экологического опыта

В экологических исследованиях отдельных растительных объектов, планктона, растительных сообществ, для выяснения правильности измерений и их объективности применяют различные математические методы. Более подробно остановимся на статистических методах [7, 10].

По завершении опыта и после получения всех данных встаёт вопрос о достаточности измеренных значений для того, чтобы делать выводы и выдвигать гипотезы. Хотя и говорят, что существуют в порядке возрастания ненадежности: вруны, заклятые лжецы и статистики, но рано или поздно приходится обращаться к статистике для истолкования полученных данных. Статистический анализ не только подтверждает полученные результаты, но, что более важно, он может реально помочь выполнению программы исследований. При умелом использовании статистики статистика поможет определить, действительно ли данные означают то, что хотелось бы получить, помогает полнее осмыслить исследование, чего иногда нельзя добиться иным путем, и часто может сэкономить время и труд, намечая последующие опыты.

Статистически достоверные числа

Для опыта требуется проведение серии измерений конечной длины стеблей растения, например, молодых растений бальзамина, произрастающих в различных экологических условиях. Мы тщательно измерили длину 11 стеблей растений линейкой с миллиметровой шкалой и каждое измерение указали в миллиметрах.

Результаты этого опыта приведены в табл. 1.

Таблица 1

Результаты опытов по измерению длины стеблей растений

Независимо от вопроса о статистической достоверности этих данных, следует рассмотреть вопрос о точности полученных числовых данных.

При измерении длины стебля очевидно наличие какой-то неустранимой погрешности, которую обычно считают равной примерно ±0,5 мм. Среднюю длину стебля в исследуемых образцах получают в каждом случае делением суммы всех полученных значений на 11. Точное деление показывает, что ни в одном случае среднее не является целым числом. Средняя длина стебля равна 15,636.... Еще один момент, который следует учесть, – это то, что измерения длины стебля, как бы их ни выражали, используют как таковые.

Если бы потребовалось довести измерения длины до крайнего значения, ее можно было бы выразить с точностью до третьего или даже до шестого знака после запятой. Это было бы бессмысленно, особенно потому, что мы знаем о наличии неустранимой погрешности измерения. Поскольку эта ошибка может составлять ±0,5 мм, вполне оправдано указание среднего значения только до первого знака после запятой или в пределах ошибки измерения, т. е. указание, что средняя длина стебля составляла 15,6 мм.

Вопрос о том, до какого знака следует рассчитывать среднюю величину – один из наиболее часто возникающих перед учеными; стандартной процедурой стало вести расчет до минимально допустимого числа знаков. За исключением особых случаев, все измерения даются не более чем до второго знака после запятой, но даже это может быть рискованным. Правилом является использование наименьшего возможного числа, причем надо быть готовым дать обоснование более чем двум цифрам после запятой [4, 7].

Рендомизация

Помимо трудностей, связанных с получением однородных экспериментальных систем, должен ‘быть решен вопрос о размещении повторностей. Даже при наилучших условиях вполне возможны небольшие колебания микроклимата (температура, свет, влажность, ветер и т. д.) на различных участках площади. Например, в полевых опытах на рост растений могут сильно влиять разница в плодородии почвы, рельеф местности, степень загрязнения и т. д. В лаборатории у многих термостатов или камер для выкрашивания также имеются различия в микроклимате от точки к точке. Поскольку необходимо иметь достаточное число повторностей для каждой переменной, чтобы численность популяции была статистически достоверной, крайне важно, чтобы все неконтролируемые переменные были устранены. Это и называется рендомизацией.

Предположим, что опыт включает 4 переменных (т.е. 4 разных концентрации ростового вещества, 4 разных сочетания азотистых субстратов, 4 разные длины волны излучения и т.д.). Предположим далее, что все они размещаются на одной и той же площади поля, термостата или камеры для выращивания. Допустим, наконец, что для каждой переменной принято по 4 повторности (или серии повторностей).

Площадь, где ведется опыт, сначала делят на 16 равных частей. Затем нумеруют все повторности (табл. 2).

Таблица 2

Один из способов избежать пристрастности в размещении повторностей заключается в том, что в шапку кладут 16 пронумерованных кусочков бумаги и размещают каждую из 16 повторностей согласно вытянутому номеру.

Второй способ называется методом латинского квадрата. Этот квадрат представляет собой распределение из п переменных X п повторностей таким образом, что каждая из , букв встречается один раз в каждом ряду и один раз в каждом столбце. В рассмотренном выше примере пХп размещение будет 4X4 (табл. 3).

Таблица 3

Могут быть латинские квадраты 5X5 и т. д., построенные таким же образом.

Разновидностью латинского квадрата является так называемый греко-латинский квадрат, где каждая из переменных имеет свой индекс. Снова взяв тот же пример из четырех переменных, можно использовать греко-латинский квадрат, для рендомизации групп повторностей в рамках переменных (табл. 4) [4, 10].

Таблица 4

Квадрат такого типа можно также увеличить до 5X5, 7X7, 10X10 и т.д., но только не 6X6.

Имеются еще варианты, которыми можно пользоваться. Некоторые ученые пользуются латинским квадратом, в котором размещение повторностей производится по ходу какой-либо шахматной фигуры, например коня или слона. Они удобны в тех , случаях, когда возможно постоянное отклонение в определенной позиции. Примером может служить квадрат 5X5, полученный ходом коня (табл.5 ).

Таблица 5

Третий способ рендомизации – использование случайных чисел. Таблицы случайных чисел состоят из ряда однозначных чисел, в которых каждое число встречается примерно с одной и то же частотой и распределение которого не подчиняется никаким закономерностям. Таблицы случайных чисел в перестановках, начиная с 6 и выше, можно найти в большинстве книг по математике. Пример можно видеть в табл. 6.

Таблица 6

Стандартные отклонения

В любой серии измерений имеется высокая степень вероятности, что не все из полученных значений будут одинаковыми в любом данном варианте. Частично это обусловлено, как мы уже видели ранее, изменчивостью, свойственной самому биологическому объекту вследствие его генетической структуры, небольшими колебаниями в окружающих условиях и в самих вариантах. К этим источникам изменчивости или неопределенности можно еще добавить ошибки измерения [5].

Обычно довольно важно уметь выразить эту изменчивость математическими или статистическими терминами так, чтобы иметь некоторое представление о рассеивании значений в ту или иную сторону от средней величины. Наиболее частым критерием рассеивания изменчивости служит так называемое стандартное (или средне-квадратичное) отклонение. Пример вычисления стандартного отклонения приведен ниже. Предположим, что подсчитывается число растений на площади 1 м, чтобы получить представление о растительном покрове большой территории. Допуская, что климат и т. д. совершенно одинаковы на всей территории, исследователь выделит 10 участков по 1 м и подсчитает числу растений на каждом из них. Полезно иметь представление о том, каковы могут быть отклонения в численности (табл. 7).

Таблица 7

Число растений на 1 м2

Среднее число растений получают, сложив все цифры в колонке и разделив их на п, т. е. число измерений: 1260: 10=126.

Хотя среднее число равно 126 растений на единицу площади, ясно, что имеются колебания от 170 до 60 растений/м2. Вычислив стандартное отклонение, можно выразить эту изменчивость.

Стандартное отклонение (часто обозначаемое сокращенно 5.0.) получают, разделив сумму всех отклонений от средней величины, возведенных в квадрат, на число наблюдений минус 1, и извлекая затем квадратный корень из этого числа. Математически это будет выглядеть так:

Д.S.=∑Δ.

Возвращаясь к рассмотренному примеру можно составить приводимую ниже табл. 8. Следует помнить, что эта операция должна быть проделана со всеми использованными числами или значениями вне зависимости от того, будут ли отклонения отрицательными или положительными, поскольку при возведении в квадрат знаки устраняются. Сумма третьей колонки составляет 8740. Это число делят затем на число измерений, уменьшенное на единицу, т. е. на п–1 = 9; отсюда 8740:9=971. Теперь для того, чтобы получить стандартное отклонение, нужно извлечь квадратный корень из 971. Для наших целей можно округлить квадратный корень из 971 до 31. Это число 31 и будет являться стандартным отклонением для десяти определений числа растений на 1 м. В таблицах его обычно приводят как среднее число плюс или минус стандартное отклонение, т. е. 126+31 растений/м2.

Таблица 8

Статистическая достоверность

В большинстве экологических опытов необходимо знать не только масштабы изменчивости в серии повторностей, но и уметь судить о том, насколько «реальны» различия, выявленные между переменными или среди них. В некоторых случаях это видно на глаз. Например, если вариант а способствует росту, а вариант 6 нет, то можно полагать, что разница между а и б реальна (если это действительно единственные переменные величины). Ответы типа «да» или «нет», хотя желательны, но их редко получают и, как правило, получают ответ типа «может быть». Оценку этого «может быть» называют определением статистической достоверности. В основном, статистическая достоверность свидетельствует о том, что имеется вероятность реальности наблюдаемых различий. Экологи, сознающие неизбежную изменчивость биологического материала и прекрасно зная, что незначительная разница в схеме опыта и условиях его проведения может сильно повлиять на результаты, решили принять лишь определенные уровни вероятности в качестве указания на реальность различий. Например, если в серии повторных опытов установлено, что вариант а отличается от варианта б только один раз из десяти, было бы глупо настаивать, что вариант а действительно отличается от варианта б. Если же, с другой стороны, вариант а дал результаты, последовательно и значительно отличающиеся от результатов в варианте б, то вероятно, что они действительно различны. Вопрос заключается лишь в том, где подвести черту [4,5,7,10].

Имеется ряд статистических методов, которыми можно пользоваться для оценки полученных данных, причем большинство их достаточно просты, чтобы оправдать их применение в большинстве экологических опытов. Математическое обоснование разных методов не входит в задачи данного исследования.

Здесь можно проиллюстрировать лишь два важных примера. Предположим, что проводится сравнение влияния интенсивности накопления свинца на удлинение стебля фасоли. Вариант а состоял из 25 растений, выращиваемых при содержании ниже кларка, а в варианте б растения выращивали при содержании выше кларка. Были приняты достаточные меры для контролирования факторов, как генетических, так и внешней среды, и рендомизации повторностей. После измерения длины стеблей были вычислены средняя длина стебля и стандартное отклонение от среднего:

Варианта а 15,0+1,4 см

вариант б 8,0 + 0,8 см

Разница между этими средними (15,0 – 8,0) равна 7,0, а среднее из двух стандартных отклонении равно 1,1. Разделив разность между средними на среднее стандартное отклонение, мы получим меру отношения оцениваемой разницы, которая в данном опыте составляет 7,0:1,1 = 6,36. Это очень большая разница, показывающая, что различия между повторностями малы по сравнению с разницей между вариантами. Чтобы определить, насколько они малы, следует обратиться к табл. 9, где указаны пределы статистической достоверности для отношений различий.

Таблица 9

Можно видеть, что разница между вариантами а и б статистически достоверна при уровне еще меньшем, чем 0,1 %.

Во втором примере ставится опыт по сравнению влияния двух источников питательных веществ на рост гриба. Снова, при достаточном числе повторностей и внимательном подходе к рендомизации и другим факторам, опыт проводят и определяют вес сухого вещества, рассчитывают, как обычно, стандартное отклонение и получают следующие результаты:

вариант а ... 18,1 ±2,1 мг сухого вещества

вариант б.... 14,7+1,9 мг сухого вещества

Здесь разница между средними равна 3,4 мг, а среднее стандартное отклонение равно 2,0. Отношение оцениваемых различий равно 3,4:2,0=1,70. Справка по таблице статистической достоверности покажет, что это отношение значимо достоверно где-то между 10 %-м и 20 %-м уровнями.

Итак, в первом опыте разница была достоверной при уровне, лучшем 0,1 %-го, в то время как во втором опыте результаты были достоверны примерно при 15 %-м уровне. Это значит, что если бы первый опыт повторили 1000 раз, то, вероятно, в 999 случаях установили бы разницу между вариантами. Короче говоря, можно быть уверенным, что наблюдаемая разница, видимо, реальна. Во втором примере повторение опыта, скорее всего, покажет, что в одном из семи опытов не будет установлено никакой разницы. Короче, нельзя быть уверенным, что разница реальна.

В экологии принято, что достоверными результатами можно считать только те, для которых уровень статистической достоверности (которая фактически является мерой вероятности) равен по меньшей мере 5 %, т. е., что только в одном из каждых 20 опытов не будет установлено разницы. Вероятность, что разница реальна, будет возрастать при уменьшении уровня до 1 %, 0,1 % и т. д.

Корреляционно-регресионный анализ в экологических системах

В экологических исследованиях более высокого ранга для выявления закономерных взаимных влияний используется корреляционно-регресионный анализ [8] и метод построения классификационных образов [9].

Построение уравнения регрессии сводится к оценке ее параметров. Для оценки параметров регрессий, линейных по параметрам, применяется метод наименьших квадратов. Он позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака у(хi) = а + bх от теоретических значений минимальна, т.е.

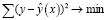. (1)

Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции, принимающий значение от [-1;1]:

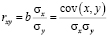(2)

Для оценки качества полученной модели используется коэффициент детерминации, который показывает долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака.

Оценка статистической значимости полученного уравнения регрессии проводится путем прохождения F-теста, который состоит в проверке гипотезы Но об отсутствии статистической значимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического Fфакт и критического (табличного) Fmaбл значения F-критерия Фишера.

Если Fmабл < Fфакт, то гипотеза Но о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность.

Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитывается t-критерий Стьюдента и доверительные интервалы каждого из показателей.

Сравнение табличного и фактического значения критерия Стьюдента осуществляется аналогично тому, как это делается с критерием Фишера.

Для расчета доверительного интервала определяется предельная ошибка для каждого показателя. Тогда доверительные границы можно установить в виде:

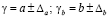(3)

В случае, если строится множественная регрессия заболеваемости по факторам у = f(x1,x2,…Хр), система нормальных уравнений МНК имеет вид:

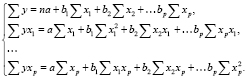(4)

Однако по коэффициентам чистой регрессии нельзя сказать, какой из факторов сильнее влияет на результат. Для этого используется уравнение регрессии в стандартизованном масштабе

,

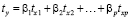где 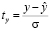– стандартизованные величины, 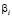– стандартизованные коэффициенты регрессии.

Связь между коэффициентами чистой регрессии и стандартизованными коэффициентаvи описывается соотношением

.

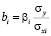Индекс множественной корреляции R [0; 1] определяется как корень квадратный из доли объясненной дисперсии, а для стандартизованных коэффициентов может быть найден по формуле

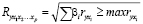(6)

При линейной зависимости коэффициент множественной корреляции можно определить через матрицу парных коэффициентов корреляции:

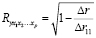, (7)

где

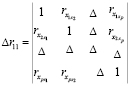
Для определения влияния на заболеваемость конкретного фактора х, при неизменном уровне других факторов применяются частные коэффициенты корреляции.

Качество построенной модели в целом определяется коэффициентом множественной детерминации, определяемым как квадрат индекса множественной корреляции .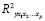

Статистическую значимость уравнения множественной регрессии в целом оценивается с помощью F-критерия Фишера.

Оценка значимости коэффициентов чистой регрессии с помощью t-критерия Стьюдента сводится к вычислению значения данного критерия.

При построении уравнения множественной регрессии может возникнуть проблема мультиколлинеарности факторов, их тесной линейной связанности. Примем, что две переменные явно коллинеарны, т.е. находятся между собой в линейной зависимости, если 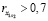. Для оценки мультиколлинеарности факторов строится матрица межфакторной корреляции.t

Основным методом, позволяющим установить взаимосвязь между уровнем заболеваемости и внешними факторами, является корреляционно-регрессионный анализ. Опыт многочисленных исследований показывает, что наиболее удобными являются парные регрессионные модели, а из множественных – те, в которых участвует не более двух или трех переменных. В качестве уравнений связи уровня заболеваемости (далее обозначается y(xi)) и внешних факторов (далее хi) могут применяться как линейные, так и нелинейные формы зависимости.

Однако многие нелинейные модели сводятся к линейным, поэтому общая теория будет рассматриваться для линейных систем.

Важным фактором, влияющим на уровень заболеваемости, является наличие в почве района различных микроэлементов в разнообразных количествах. Однако построение многофакторной модели в данном случае нерационально в силу высокой трудоемкости модели и ее низкой точности.

По данным проведенных исследований сельскохозяйственных угодий района, для Кинель-Черкасского района имеются непрерывные данные по содержанию в почве микро- и макроэлементов за период с 1997 по 2011 гг. [1,3,6].

Исходные данные для построения регрессионной модели приведены в приложении 1.

Для уточнения картины заболеваемости была проведена работа по установлению связи между основными геохимическими параметрами территории и уровнем заболеваемости за длительный период (1997–2011 гг.) с помощью множественной линейной регрессии [9]. В качестве действующих на заболеваемость факторов {Xi}, были выбраны 8 рядов макро- и микроэлементов, концентрация которых в почвах района измерялась в мг/кг, а заболеваемость – Y – случаев в год. Анализируя заболеваемость группы кардиологические заболевания, отмечается наиболее высокий уровень корреляции между заболеваемостью и концентрацией азота в почвах (0,830; прямая), а также с концентрацией серы (–0,841; обратная). Значительная корреляция (–0,746:обратная) между кардиологическими заболеваниями и кобальтом, однако ее значение ниже. Связь оценивается как существенная.

Анализируя заболеваемость группы новообразования, отмечается наиболее высокий уровень корреляции между заболеваемостью и концентрацией азота (0,915:прямая), а также с концентрацией серы (–0,883;обратная). Корреляция между новообразованиями и кобальтом (–0,578; обратная) низка, что особенно интересно, так как большинство исследователей на других территориях получают другие результаты. Помимо регрессии по калию и сере, объясняющей 89 % вариации заболеваемости, автором была проведена попытка построения четырехмерной регрессии по калию (Х2), сере (Х4) марганцу (Х5), кобальту (X8). Объясняющие факторы покрывают 91,1 % дисперсии заболеваемости. Стандартизированные коэффициенты регрессии говорят о том, что все перечисленные факторы влияют на снижение заболеваемости Новообразованиями, т.к. все коэффициенты имеют отрицательный знак. Наиболее эффективным регулятором является сера (-1,013), на втором месте по значимости – калий (- 0,322), далее марганец (-0,129). Крайне незначительное влияние имеет кобальт.

Анализируя заболеваемость группы болезни органов дыхания, не выявляется яркой корреляции между проявлениями заболеваний этой группы и концентрациями микроэлементов. Это свидетельствует в пользу того, что причины заболеваний этой группы нужно искать в климатической составляющей. Тот факт, что некоторая связь все же имеется, объясняется тем, что иммунная реакция организма зависит от наличия в почве и в питании человека микро- и макроэлементов.

Анализируя заболеваемость группы болезни органов пищеварения, отмечается наиболее высокий уровень корреляции между заболеваемостью и концентрацией азота в почвах (0,821; прямая), а также с концентрацией серы (–0,881;обратная). Корреляция между болезнями органов пищеварения и кобальтом (–0,515;обратная), а также между болезнями органов пищеварения и марганцем в почвах (0,333; прямая).

Анализируя заболеваемость группы инфекционные и паразитарные, отмечается наиболее высокий уровень корреляции между заболеваемостью и концентрацией калия в почвах (0,494; прямая), однако этот уровень недостаточен для объяснения. Отсюда следует, что объяснение группе инфекционные и паразитарные связано миграциями паразитических элементов из Похвистневского природно-эпидемического очага с перемещающимися животными, прежде всего мышевидными грызунами и лисами.

Анализируя группы диагнозов кардиологические заболевания, новообразования и болезни органов пищеварения, прослеживается следующая закономерность: для всех этих групп диагнозов большое значение имеет концентрация калия и серы.

Построение классификационных образов

Для более полного и комплексного анализа связи заболеваемости населения с ландшафтами можно провести построение классификационных образов на основе алгоритма кратчайшего расстояния [9].

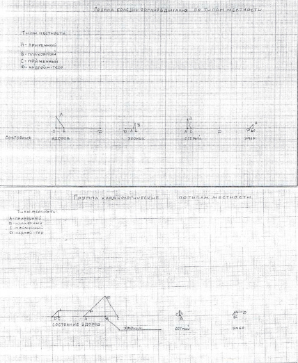
В качестве объектов здесь выступают типы местности Кинель-Черкасского района: А – приречный, В – плакорный, С – пойменный, D – надпойменно-террасовый [2]. Для каждого типа местности вычислено среднее по выборке значение вероятности нахождения особи в различных состояниях – «здоров», «умер», «острый», «хроник» – рассчитанных на основе марковских процессов. Именно вследствие осреднения на средних величинах не наблюдается столь же значительных различий между типами местности, как в случае анализа территориального размещения вероятностей.

В качестве пространства состояний выбрана плоскость (х, у), где х – вероятность нахождения организма в определенном состоянии через 1 год, у – вероятность нахождения организма в том же состоянии через 2 года после начала прогнозирования.

В качестве меры различия выбрано классическое евклидово расстояние между двумя объектами вида

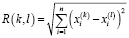
где k, l – сравниваемые объекты или классы, х -признак объекта, n – количество признаков сравнения (приложение 2).

Выводы

Был выполнен обзор существующих литературных источников по проблеме применения математических методов в экологии и выбраны для примера некоторые из них.

Экологические факторы влияют на объекты разного ранга и их объективная оценка возможна только с помощью математических методов.

Выявленные, математически достоверные связи, между отдельными заболеваниями и геохимическим фоном в почвах Кинель-Черкасского района, можно использовать в практических целях. Например, для внесения соответствующих удобрений. Это повлияет на уровень заболеваемости и затрагивает сразу два национальных проекта «Развитие АПК» и «Здоровье».

Подобного рода работы очень актуальны: системны, разноплановы, обоснованы. Другое дело, что реализация научных разработок – дело дорогостоящее и требует взвешенных, коллективных решений на уровне региональных властей. В любом случае, дорогу пройдёт идущий.

Приложение 1

Влияние микроэлементов на заболеваемость в Кинель-Черкасском районе

Приложение 2

Классификационные образы по типам местности

Библиографическая ссылка