Современная жизнь делает задачи на проценты актуальными, так как сфера практического приложения процентных расчетов расширяется. Вопросы инфляции, повышение цен, рост стоимости акций, снижение покупательской способности касаются каждого человека в нашем обществе. Планирование семейного бюджета, выгодного вложения денег в банки, невозможны без умения производить несложные процентные вычисления.
Без понятия «процент» нельзя обойтись ни в бухгалтерском учёте, ни в финансовом анализе, ни в статистике.
Проценты – математическое понятие, которое часто встречается в повседневной жизни. Любой человек должен уметь решать задачи, предлагаемые самой жизнью. Мы платим налоги. Как посчитать материальное вознаграждение, которое получаем мы, когда кладем деньги на депозит, какое вознаграждение получает банк, когда мы берем кредит, ипотеку. Все эти и многие другие вопросы, касающиеся процентных исчислений, решает знание процентов и умение решать задачи на проценты.
Везде – в газетах, по радио, телевидению и на работе обсуждаются повышение цен, зарплат, пенсии, рост стоимости акций, снижение покупательской способности населения. Так, мы часто слышим или читаем, что, например, цены повысились на 20 %, молоко содержит 4 % жира, пенсия повысилась на 10 %, в выборах приняли участие 76 % избирателей.
Чтобы начислить зарплату работнику, нужно знать процент налоговых отчислений; чтобы открыть депозитный счёт в сбербанке, нужно знать размеры процентных начислений на сумму вклада; чтобы знать приблизительный рост цен в будущем году, мы интересуемся процентом инфляции.
Решение математических задач практического содержания позволяет убедиться в значении математики для различных сфер человеческой деятельности, увидеть широту возможных приложений математики, понять её роль в современной жизни.
Мои наблюдения и проведённый опрос среди одноклассников и друзей показали, что мы, школьники, молодые люди, имеем самые общие и довольно небольшие знания о процентах, а о различных способах исчисления процентов и того меньше.
Выявленные недостатки в наших знаниях и умениях решать задачи на проценты объясняются наличием объективно складывающихся противоречий: между существующей потребностью вычислять процентное содержание в различных областях жизни людей и – не информированностью по этому вопросу и почти полным неумением это быстро и легко сделать.
С учётом выявленных противоречий была сформулирована проблема исследования: каковы история и способы решения задач на проценты?
Актуальность проблемы, её значимость в современном мире определили тему моего исследования: «Решение задач на проценты».
Цель исследования: изучить сведения о процентах, о типах задач, о способах их решения и научиться использовать полученные знания на практике.
Объект исследования: Проценты в прошлом и в настоящее время.
Предмет исследования: исторические сведения о процентах, решение задач на проценты и процентное содержание, концентрацию, смеси и сплавы с преимущественным использованием основных правил действия с десятичными и обыкновенными дробями.
В соответствие с целью исследования были поставлены следующие задачи исследования:
1. Изучить историю понятия ПРОЦЕНТ.
2. Рассмотреть использование процента в повседневной жизни.
3. Рассмотреть различные типы задач и их решения.
4. Устранить пробелы в знаниях по решению основных задач на проценты: нахождение процента от величины, нахождение величины по её проценту, нахождение процента одной величины от другой.
5. Обобщить полученные знания и умения и сформулировать выводы.
В работе использовались следующие методы исследования: изучение литературы по теме, анализ, синтез, обобщение.
Актуальность процентов от древности до наших дней
История развития «процента»
Изучение информации в сети интернет показало, что слово «процент» происходит от латинского слова «procentum», что означает «со ста». Идея выражения частей целого постоянно в одних и тех же долях родилась ещё в древности у вавилонян. В их клинописных табличках уже содержались задачи на расчёт процентов. Были известны проценты и в Индии, где с давних пор вёлся счёт в десятичной системе счисления. Индийские математики вычисляли проценты, применяя так называемое тройное правило, т.е. пользуясь пропорцией. Они умели производить и более сложные вычисления с применением процентов.
В русском языке слово «процент» имеет и другое смысловое значение – выражает тот факт, что заёмщик помимо возврата предоставленных ему кредитором денежных средств должен дополнительно заплатить кредитору за использование этих средств. Об этом говорит, например, объявление: «Банк предоставляет населению кредиты под проценты».
Денежные расчеты с процентами были особенно распространены в Древнем Риме. Римляне называли процентами деньги, которые платил должник заимодавцу за каждую сотню. Даже римский сенат вынужден был установить максимально допустимый процент, взимаемый с должника, так как некоторые заимодавцы усердствовали в получении процентных денег. От римлян проценты перешли к другим народам.
В средние века в Европе в связи с широким развитием торговли особенно много внимания обращали на умение вычислять проценты. В то время приходилось рассчитывать не только проценты, но и проценты с процентов, т.е. сложные проценты, как называют их в наше время. Отдельные конторы и предприятия для облегчения труда при вычислениях процентов разрабатывали свои особые таблицы, которые составляли коммерческий секрет фирмы.
В Европе десятичные дроби появились на 1000 лет позже, их ввел бельгийский ученый Симон Стевин. В 1584 г. он впервые опубликовал таблицу процентов. Введение процентов было удобным для определения содержания одного вещества в другом; в процентах стали измерять количественное изменение производства товара, рост и спад цен, рост денежного дохода и т.д.
Знак « %» происходит, как полагают, от итальянского слова cento(сто), которое в процентных расчётах часто писалось сокращённо cto. Отсюда путём дальнейшего упрощения буквы t в наклонную черту произошёл современный символ для обозначения процента.
Другая версия происхождения этого знака заключается в том, что в Париже в 1685 году наборщик книги-руководства по коммерческой арифметике допустил опечатку – вместо ctoнаписал %.
Долгое время под процентами понимались исключительно прибыль или убыток на каждые 100 рублей. Они применялись только в торговых и денежных сделках. Уже в далекой древности широко было распространено ростовщичество – выдача денег под проценты. Разность между той суммой, которую возвращали ростовщику, и той, которую первоначально взяли у него, называлась лихвой. Так, в Древнем Вавилоне она составляла 20 % и более! Известно, что в XIV-XV вв. в Западной Европе широко распространились банки – учреждения, которые давали деньги в долг князьям, купцам, ремесленниками и т. д. Конечно, банки давали деньги не бескорыстно: за пользование предоставленными деньгами они брали плату, как и ростовщики древности. Эта плата выражалась обычно в виде процентов к величине выданных в долг денег. Затем область их применения расширилась, проценты встречаются в хозяйственных и финансовых расчетах, статистике, науке и технике.
Ныне процент – это частный вид десятичных дробей, сотая доля целого (принимаемого за единицу). Процентами очень удобно пользоваться на практике, так как они выражают части целых в одних и тех же долях. Это дает возможность упрощать расчеты и легко сравнивать части между собой и с целым.
Процент – сотая доля числа, принимаемого за целое. Если речь идет о проценте от данного числа, то это число и принимается за 100 %.
Например, 1 % от зарплаты – это сотая часть зарплаты; 100 % зарплаты – это сто сотых частей зарплаты, т. е. вся зарплата. Сотая часть метра – это сантиметр, сотая часть центнера – это килограмм.1 % – одна сотая доля числа.
Как известно из практики, с помощью процентов часто показывают изменение той или иной конкретной величины. Такая форма является наглядной числовой характеристикой изменения, характеризующей значимость произошедшего изменения. Величина, выраженная в процентах, является более наглядной, понятной, ее легко сравнить с другими значениями.
«Проценты» в повседневной жизни
Мы считаем, что в настоящее время актуально более углубленное изучение темы «Проценты» в разных ситуациях. Причина такой необходимости – это значимость, т.к. задания по данной теме часто встречаются на различных экзаменах, а также применяются не только на уроках математики, химии, экономики. Проценты прочно входят и в нашу повседневную жизнь: кредиты, банковские проценты, составы химических веществ.
Для полного исследования применения процентов в нашей жизни я провела опрос среди моих одноклассников, где они встречали это понятие. Результаты опроса удивили даже самих ребят. Совместно мы вспомнили так много сфер применения процента вот перечень приведённых примеров:
Проценты применяются:
При расчёте скидок в магазине, составлении договора в банке, определении остроты зрения, соотношения ниток в составе ткани, определении жирности в продуктах, определении загрузки программ в компьютере или зарядки элементов питания, значение соотношения голосов на выборах или при голосовании, при распределении прибыли фирмы, подсчёте выполнения тестов ЕГЭ, расчёт налогов от з/платы, при сборе урожая и определении его потерь от стихии, соотношение воды в организме человека, или воды и суши на Земле, в соотношении примесей и золота в украшениях, поступивших в ВУЗы от общего чиста поступающих, информация для автомобилиста об остатке бензина в баке, при рейтинге участников хит-парада, определении порога эпидемии.
Из вышесказанного видно, что проценты применяются в следующих областях: торговле, программировании, экономике, технологии производства, статистике, медицине, общественной жизни, бытовой жизни, разных областях науки, искусстве.
Проценты являются неотъемлемой частью банковских, торговых, налоговых, фармацевтических и т.д. операций. Они вошли в нашу жизнь не только с выпечкой кулинарных изделий и с приготовлением лакомств, они буквально атакуют нас в пору рыночных отношений в экономике, в пору банкротств, инфляций, кризисов.
Вкладчик сбережений в банке учится жить на проценты, грамотно размещая деньги в прибыльное дело. Правильно воспользоваться ипотечным кредитом в банке также помогут проценты. Грамотно проводить процентные расчеты – это значит иметь выгоду в банковских сделках, иметь рентабельный бизнес и коммерческие предложения.
Таким образом, проценты – это одно из математических понятий, которые очень часто встречаются в повседневной жизни.
После опроса стало окончательно ясно, что без умения понимать такого рода информацию в современном обществе, просто трудно было бы существовать. Поэтому возникает необходимость выявить и изучить все существующие задачи на проценты и способы их решения, что мы и раскроем в следующем параграфе.
Виды задач на проценты и способы их решения
Виды задач на проценты
Нахождение процентов от числа
Чтобы найти процент от числа, следует:
1. Проценты записать десятичной дробью.
2. Число умножить на эту десятичную дробь.
Задача: В магазин привезли 14 т капусты, 70 % всей капусты продали. Сколько тонн капусты осталось?
Решение:
Оставшаяся часть капусты составляет: 100 % – 70 % = 30 % = 0,3
14 · 0,3 = 4,2
Ответ: 4,2 тонны.
Нахождение числа по его процентам
Чтобы найти число по его процентам, следует:
1. Проценты записать десятичной дробью;
2. Число разделить на эту десятичную дробь.
Задача: Тракторная бригада вспахала за день 25 % всего поля, что составляет 60 га. Какова площадь всего поля?
Решение:
25 % = 0,25;
60 : 0,25 = 240
Ответ: 240 га.
Нахождение процентного отношения чисел
Чтобы узнать, сколько процентов одно число составляет от второго, следует:
1. Первое число разделить на второе.
2. Результат умножить на 100 %.
Задача: Длина прямоугольника 40 дм, площадь 200 дм2. Сколько процентов составляет ширина от длины?
Решение:
ширина равна 200 : 40 = 5
5:40 ·100 % = 12,5 %
Ответ: 12,5 %
Увеличение на р %
Чтобы увеличить положительное число а на р %, следует:
умножить число а на коэффициент увеличения к = (1 + 0,01р)
Задача: Цена на яблоки выросла на 30 %. Какова цена яблок после повышения, если первоначальная цена 250 рублей?
Решение:
к = 1 + 0,01 ·30 = 1,3
250 · 1,3 = 325
Ответ: 325 рубля.
Уменьшение на р %
Чтобы уменьшить положительное число а на р %, следует:
умножить число а на коэффициент уменьшения к = (1- 0,01·р)
Задача: Цена на путевку в санаторий снизилась на 10 %. Сколько стоит путевка, если ее первоначальная цена 12 рублей?
Решение:
к = 1 – 0,01·10 = 0,9;
12 · 0,9 = 10,8
Ответ: 10,8 рубля.
Решение задач на проценты составлением пропорции
При решении задач на проценты некоторая величина b принимается за 100 %, а ее часть – величина a – принимается за x % и составляется пропорция:
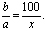
Из пропорции по двум известным величинам определяют неизвестную третью величину, пользуясь основным свойством пропорции: b·x = 100·a
Задача 1. В театральной студии занимаются 36 девушек. Сколько всего учащихся занимаются в данной студии, если юноши составляют 52 %?
Решение:
Девушки составляют 100 % – 52 % = 48 % всех учащихся.
Девушки: 36 чел. – 48 %
Всего учащихся: х чел. – 100 %
Составляем пропорцию:
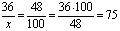
Ответ: 75 учащихся.
Задача 2. Зарплату токарю повысили сначала на 10 %, а затем через год еще на 20 %. На сколько процентов повысилась зарплата токаря по сравнению с первоначальной?
Решение:
а – первоначальная зарплата
1 после повышения на 10 % – 1,1 а
через год после повышения на 20 % – 1,1а · 1,2 = 1,32а
Составим пропорцию:
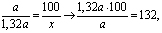
132 % – 100 % = 32 %
Ответ: на 32 %.
Решение задач на проценты алгебраическим методом
Задача 1. Одна сторона прямоугольника на 42 % больше другой. Площадь прямоугольника 568 см2. Найти наименьшую из сторон.
Решение:
Пусть х – одна сторона прямоугольника, тогда вторая сторона будет 1,42х.
Составим уравнение и решим его:
х · 1,42 х = 568
1,42х2 = 568
х2 = 400
х1 = 20 и х2 = – 20 – не подходит
Ответ: 20 см.
Задача 2. Турист прошел в первый день 40 % маршрута, во второй день 45 % оставшегося пути, после чего ему осталось пройти на 6 км больше, чем он прошел во второй день. Весь маршрут составляет
Решение:
х (км) – весь маршрут
0,4 х (км) – турист прошел в первый день пути
0,45(х – 0,4х) = 0,27х (км )– турист прошел во второй день пути
х – (0,4х + 0,27х) = 0,33х (км) – осталось пройти туристу
Т.к. туристу осталось пройти на 6 км больше, чем он прошел во второй день, составим уравнение и решим его:
0,33х – 0,27х = 6
0,06х = 6
х = 100
Ответ: 100 км.
Решение задач на концентрацию и процентное содержание
Для решения задач из этого раздела введем основные понятия:
Пусть даны два различных вещества А и В с массами mА и mВ. Масса смеси, составленной из этих веществ, равна М = mА + mВ.
Массовая концентрация вещества А в смеси (доля чистого вещества в смеси)
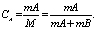
Массовые концентрации связаны равенством: СА + СВ = 1
Процентное содержание вещества А в данной смеси вычисляется по формуле:
РА = СА · 100 %
Задача 1. Имеется 50г раствора, содержащего 8 % соли. Надо получить 5 %-й раствор. Чему равна масса пресной воды, которую необходимо добавить к первоначальному раствору?
Решение:
Пусть требуется добавить хкг пресной воды. За чистое вещество принимаем соль. Решение оформим таблицей.
|
Состояние смеси |
Количество чистого вещества mА = М · СА |
Общее количество смеси М |
Массовая концентрация СА |
|
1 |
0,08 · 50 |
50 |
0,08 |
|
добавление |
0,08 · 50 |
50 + х |
0,05 |
Составим уравнение:
0,08 · 50 = (50 + х) · 0,05
50 + х = 80
x = 30> x = 30
Ответ: 30 кг.
Задача 2. В растворе содержится 15 % соли. Если добавить 150г соли, то в растворе будет содержаться 45 % соли. Найти массу соли в первоначальном растворе.
Решение:
Пусть масса раствора – х г. Решение оформим таблицей.
|
Состояние смеси |
Количество чистого вещества mА = М · СА |
Общее количество смеси М |
Массовая концентрация СА |
|
1 |
0,15х |
х |
0,15 |
|
2 |
0,15х + 150 |
х + 150 |
0,45 |
Составим и решим уравнение:
0,15х + 150 = (х + 150) · 0,45
0,3х = 82,5 >
х = 275
Найдем массу чистого вещества в первоначальном растворе:
275 · 0,15 = 41,25.
Ответ: 41,25 г.
Нами рассмотрено 8 видов задач на проценты. Как показывает анализ, в экзаменационных работах по ОГЭ включены задачи на проценты, некоторые из них представлены в приложении.
Заключение
В заключение хочется сказать, проценты – это одна из сложнейших тем математики, и очень многие учащиеся затрудняются или вообще не умеют решать задачи на проценты. А понимание процентов и умение производить процентные расчёты, необходимы для каждого человека, так как с процентами мы сталкиваемся в повседневной жизни постоянно. Поэтому считаю, что моя работа найдет практическое применение на уроках алгебры, как пример решения задач разных видов с практическим содержанием. Поможет выпускникам вспомнить основные способы решения задач на проценты.
Приложение
Задачи на проценты в вариантах ОГЭ по математике
1) Городской бюджет составляет 45 млн. р., а расходы на одну из его статей составили 12,5 %. Сколько рублей потрачено на эту статью бюджета?
Решение:
Переведем 45 млн в рубли = 45000000, так как 45 млн весь бюджет следовательно – 100 %, так как на статью было затрачено 12,5 % от общего бюджета, обозначим через х это кол-во в рублях, составим пропорцию
45000000 – 100 %
х – 12,5 %
х = 45000000·12,5:100=5625000 (руб.)
Ответ: 5625000 (руб.)
2) Перед представлением в цирк для продажи было заготовлено некоторое количество шариков. Перед началом представления было продано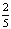 
всех воздушных шариков, а в антракте – еще 12 штук. После этого осталась половина всех шариков. Сколько шариков было первоначально?
Решение:
Пусть осталось шариков х.
Все шарики 2х
Продали перед представлением:
2х· 
= 2х·0,4 = 0,8х
Продали в антракте 12 штук
составим уравнение
2х – 0,8х – 12 = х
2х – 0,8х – х = 12
0,2x = 12
x = 12:0,2
х = 60 шариков осталось
60·2 = 120 шариков было
Ответ:120 шариков
3) Сберегательный банк начисляет на срочный вклад 20 % годовых. Вкладчик положил на счет 800 р. Какая сумма будет на этом счете через год, если никаких операций со счетом проводиться не будет?
Решение:
Через год вкладчик получит 20 % дохода, что составит
800·0,2 = 160 р.
Таким образом, через год на счете будет:
800 + 160 = 960 р.
Ответ: 960 р.
4) Товар на распродаже уценили на 20 %, при этом он стал стоить 680 р. Сколько стоил товар до распродажи?
Решение:
100 – 20 = 80 % новая цена составляет 80 % от старой цены.
Cоставим пропорцию
680 рублей – 80 %
x рублей – 100 %
680·100:80 = 850 рублей стоил товар до распродажи
Ответ: 850 рублей.
5) Государству принадлежит 60 % акций предприятия, остальные акции принадлежат частным лицам. Общая прибыль предприятия после уплаты налогов за год составила 40 млн. р. Какая сумма из этой прибыли должна пойти на выплату частным акционерам?
Решение:
Один процент от 40 млн. равен: 40 000 000:100 = 400 000 руб.
На выплату частным акционерам пошло: 400 000·40 = 16000000 руб.
Ответ: 16000000.
6) Акции предприятия распределены между государством и частными лицами в отношении 3:5. Общая прибыль предприятия после уплаты налогов за год составила 32 млн. р. Какая сумма из этой прибыли должна пойти на выплату частным акционерам?
Решение:
Пусть x млн. рублей приходится на одну часть акции, тогда 5x приходится частным акционерам, а 3x – государству. Зная, что вся прибыль составила 32 млн. рублей, составим уравнение:
3x + 5x = 32
8x = 32
x = 4 млн руб.
Таким образом, частным акционерам приходится в пять раз больше или 20 млн. руб.
Ответ: 20 000 000.
7) Число хвойных деревьев в парке относится к числу лиственных как 1:4. Сколько процентов деревьев в парке составляют лиственные?
Решение:
Всего деревьев пять частей, из них лиственных – четыре части, это составляет 4 : 5 = 0,8 или 80 %.
Ответ: 80.
8) Средний вес мальчиков того же возраста, что и Сергей, равен 48 кг. Вес Сергея составляет 120 % среднего веса. Сколько весит Сергей?
Решение:
Найдем вес Сергея: 48·120:100 = 57,6 кг.
Ответ: 57,6 кг.
9) В начале года число абонентов телефонной компании «Север» составляло 200 тыс. чел., а в конце года их стало 210 тыс. чел. На сколько процентов увеличилось за год число абонентов этой компании?
Решение:
Обозначим за 100 % число абонентов в 200 тыс. чел., а за х – 210 тыс. чел. абонентов.
Составим пропорцию:
200 тыс. чел. – 100 %
210 тыс. чел. – х %
х = 210·100/200 = 105 ( %)
105 % – 100 % = 5 % (на столько процентов увеличилось количество абонентов)
Ответ: 5 %
10) Тест по математике содержит 30 заданий, из которых 18 заданий по алгебре, остальные – по геометрии. В каком отношении содержатся в тесте алгебраические и геометрические задания?
Решение:
Количество заданий по геометрии равно: 30-18=12 шт. Таким образом, алгебраические и геометрические задачи находятся в отношении: 18 : 12 = 3 : 2.
Ответ: 3 : 2
11) На счет в банке, доход по которому составляет 15 % годовых, внесли 24 тыс. р. Сколько тысяч рублей будет на этом счете через год, если никаких операций со счетом проводиться не будет?
Решение:
Найдем, сколько процентов будет через год: 100 %+15 %=115 %. Таким образом, через год в банке будет: 2400·115:100=27600 руб.
Ответ: 27600 руб.
12) Какая сумма (в рублях) будет проставлена в кассовом чеке, если стоимость товара 520 р., и покупатель оплачивает его по дисконтной карте с 5 %-ной скидкой?
Решение:
Рассчитаем скидку, которую получает покупатель, оплачивая товар по дисконтной карте с 5 %-ной скидкой: 520·5:100=26 руб. Таким образом, итоговая цена со скидкой равна: 520 – 26 = 494 руб.
Ответ: 494.
13) В понедельник некоторый товар поступил в продажу по цене 1000 р. В соответствии с принятыми в магазине правилами цена товара в течение недели остается неизменной, а в первый день каждой следующей недели снижается на 20 % от предыдущей цены. Сколько рублей будет стоить товар на девятый день после поступления в продажу?
Решение:
Как известно, в неделе 7 дней. Значит, 12 день выпадает на вторую неделю, когда цена снижается на 20 %, таким образом, товар будет стоить 80 %. Имеем:
1000·80:100 = 800
Ответ: 800.
14) В период распродажи магазин снижал цены дважды: в первый раз на 30 %, во второй – на 50 %. Сколько рублей стал стоить чайник после второго снижения цен, если до начала распродажи он стоил 700 р.?
Решение:
В первый раз цена упала на 700 · 30:100 = 210 руб. Значит, после первого понижения цен чайник стал стоить 700 – 210 = 490 руб. Во второй раз цена упала на 490 · 45:100 = 220,5 руб. Значит, после второго понижения цен чайник стал стоить 490 – 220,5 = 269,5 руб.
Ответ: 269,5.
15) При оплате услуг через платежный терминал взимается комиссия 5 %. Терминал принимает суммы кратные 10 рублям. Николай хочет положить на счёт своего мобильного телефона не меньше 320 рублей. Какую минимальную сумму он должен положить в приемное устройство данного терминала?
Решение:
С учетом комиссии, Аня должна внести в приемное устройство сумму не менее 300 + 300 · 0,05 = 315 рублей. Значит, минимальная сумма, которую должна положить Аня в приемное устройство данного терминала – 320 рублей. Проверим, что этой суммы достаточно: 5 % от нее составляют 16 руб. (это комиссия), оставшиеся 304 рубля пойдут на счет телефона.
Ответ: 320.
16) Мобильный телефон стоил 5000 рублей. Через некоторое время цену на эту модель снизили до 3000 рублей. На сколько процентов была снижена цена?
Решение:
Цену на телефон снизили на 5000 – 3000 = 2000 рублей. Разделим 2000 на 5000:
2000:5000 = 0,4.
Значит, цену снизили на 40 %.
Ответ: 40.
17) На покупку планшета взяли кредит 20000 р на 1 год под 16 % годовых. Вычислите, сколько денег необходимо вернуть банку, какова ежемесячная сумма выплат?
Решение:
20000·16:100 = 3200 (руб.) – один год
20000 + 3200 = 23200 (руб.) – полная сумма с процентами
23200:12= 1933 (руб.) – ежемесячная сумма выплат
Ответ: 1933 рубля.
18) Пачка чая стоила 100 рублей. Сначала цену повысили на 10 %, а затем снизили на 10 % (от новой цены). Сколько теперь стоит пачка чая?
Решение:
Так как цену повысили на 10 %, значит нужно умножить первоначальную цену на 1,1 и при понижении на 10 % нужно умножить на 0,9,
100·(1 + 0,1) ·(1 – 0,1) = 99 руб.
Ответ: 99 рублей.
19) В сентябре 1 кг винограда стоил 60 рублей, в октябре виноград подорожал на 25 %, а в ноябре еще на 20 %. Сколько рублей стоил 1 кг винограда после подорожания в ноябре?
Решение:
В октябре виноград подорожал на 60 · 25:100 = 15 рублей и стал стоить 60 + 15 = 75 рублей. В ноябре виноград подорожал на 75 ·20:100 = 15 рублей. Значит, после подорожания в ноябре 1 кг винограда стоил 75 + 15 = 90 рублей.
Ответ: 90
20) В школе 800 учеников, из них 30 % – ученики начальной школы. Среди учеников средней и старшей школы 20 % изучают немецкий язык. Сколько учеников в школе изучают немецкий язык, если в начальной школе немецкий язык не изучается?
Решение:
Учеников начальной школы 800 · 30:100 = 240, а учеников средней и старшей школы – 800 – 240 = 560. Значит, немецкий язык в школе изучают 560 · 20:100 = 112 учеников.
Ответ: 112.
Библиографическая ссылка
Вострецова Я.А. ПРОЦЕНТЫ. РЕШЕНИЕ ЗАДАЧ НА ПРОЦЕНТЫ // Международный школьный научный вестник. – 2017. – № 6. ;URL: https://school-herald.ru/ru/article/view?id=460 (дата обращения: 03.12.2024).