Друзья, вопрос банальный: можно ли ездить на квадратных колесах? Ответ не менее банальный: нет нельзя. Можно, конечно, но будет сильно трясти. Вопрос другой: можно ли ездить на треугольных колесах? Ответ: нельзя, будет сильно трясти. Так вот – неправильно. Смотря, на каких треугольниках. Есть один треугольник на свете, на котором вполне можно прокатиться. Но этот треугольник необычный, он называется треугольник Рёло.
Современные инженеры, можно сказать, постоянно изобретают велосипед, внося все новые усовершенствования в его конструкцию и отдельные детали. Однажды в интернете я увидел фотографию необычного велосипеда, а потом прочитал об одном удивительном изобретении китайского пенсионера – велосипеде с треугольными колесами. Меня заинтересовало не только само по себе данное изобретение, но и необычная геометрическая фигура – круглый треугольник. Теперь я знаю, что он называется треугольником Рёло и посвятил свою работу изучению его свойств и областей применения. А заодно поставил задачу выяснить, как геометрия позволяет этому чуду катиться и иметь удивительно плавный ход.
Объект исследования: треугольник Рёло
Предмет исследования: понятие треугольника Рёло и практическое применение свойств треугольника Рёло.
Цель: изучить основные свойства треугольника Рёло, сборка модели средства передвижения с колесами в форме треугольника Рёло. Привести достаточное количество примеров применения свойств треугольника Рёло.
Задачи:
1. Изучить главные свойства и узнать как можно больше о треугольнике Рёло.
2. Познакомиться с историей изобретения.
3. Рассмотреть области применения фигур постоянной ширины.
4. Найти объяснение плавности хода велосипеда с «треугольными колесами»
Методы работы: изучение научной литературы, наблюдение, анализ, эксперимент.
Понятие треугольника Рёло
Итак, что же такое «круглый» треугольник? Треугольник Рёло представляет собой область пересечения трёх равных кругов с центрами в вершинах правильного треугольника и радиусами, равными его стороне. Треугольник Рёло можно построить с помощью одного только циркуля, не прибегая к линейке. Это построение сводится к последовательному проведению трёх равных окружностей. Центр первой выбирается произвольно, центром второй может быть любая точка первой окружности, а центром третьей — любая из двух точек пересечения первых двух окружностей.
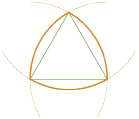
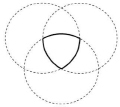

Треугольник Рёло плоская выпуклая геометрическая фигура, простейшая после круга фигура постоянной ширины.
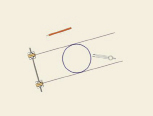
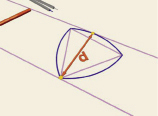
круг треугольник Рёло
Как и в случае окружности проведем две касательные, зафиксируем расстояние между ними и начнем их вращать. Треугольник Рёло постоянно касается обеих прямых. Действительно, одна точка касания всегда расположена в одном из «углов» треугольника Рёло, а другая на противоположной дуге окружности. Значит, ширина всегда равна радиусу окружностей, т.е. длине стороны изначального правильного треугольника.
Если добавить пару параллельных прямых, касающихся треугольника Рёло и образующих с уже имеющимся углом прямой угол, то получится квадрат. Если вращать треугольник Рёло специальным образом, то он постоянно будет находиться внутри квадрата и в любой момент времени касаться всех его сторон. Но квадрат этот будет иметь немного скругленные углы.

История изобретения треугольника Рёло
Изучив научную литературу в Интернет-ресурсе, я узнал, что название фигуры происходит от фамилии немецкого механика Франца Рёло (1829 – 1905). Наверное, именно он был первым, кто исследовал свойства этого треугольника и использовал его в своих механизмах. В 1852 г. он окончил политехникум в Карлсруэ, с 1856г. был профессором Политехнического института в Цюрихе, а в 1864–1896 г. профессором Промышленного института (позже – Высшая техническая школа) в Берлине.

Рёло не является первооткрывателем этой фигуры, хотя он и подробно исследовал её.
Иные исследователи первооткрывателем этой фигуры называют Леонарда Эйлера(XVIII век), который уже тогда продемонстрировал возможность его создания из трех окружностей.
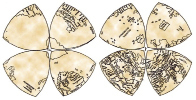
А третьи «увидели» треугольник Рёло в рукописях Леонардо да Винчи. Созданная им карта мира имеет вид четырех сферических треугольников. В 1514 г. Леонардо да Винчи создал одну из первых в своём роде карт мира. Поверхность земного шара на ней была разделена экватором и двумя меридианами (угол между плоскостями этих меридианов равен 90 °) на восемь сферических треугольников, которые были показаны на плоскости карты треугольниками Рёло, собранными по четыре вокруг полюсов.
Свойства треугольника Рёло. Кривые постоянной ширины
Треугольник Рёло – также как и круг – кривая постоянной ширины. У круга ширина в любом направлении одна и та же: она равна диаметру круга. Треугольник Рёло имеет постоянную ширину, равную стороне исходного треугольника.
Данные утверждения проверены опытным путем, вращением трех геометрических фигур между двумя опорными прямыми:


Доказательство постоянства ширины
Периметр треугольника Рёло
Одно из удивительных и трудно доказываемых свойств состоит, в том, что все кривые одной и той же постоянной ширины а имеют одинаковые периметры. Формула P = πa доказана опытным путем, в математике носит название теоремы Барбье.
Для доказательства этого свойства я вырезал из полистирола треугольник Рёло и круг, диаметр которого равен длине стороны треугольника. С помощью мягкой ленты нашел периметры моих моделей и путем измерения длины этой ленты убедился в справедливости теоремы Барбье.




Определение периметра круга и треугольника Рёло
Могут ли колеса средств передвижения быть некруглыми
Изобретением велосипеда занимается китайский рационализатор Гуань Байхуа (Guan Baihua), 50-летний офицер из города Циндао. Больше того, он изобретает заново самую консервативную деталь велосипеда – колеса. Вместо понятных всем круглых он предложил кататься на колесах пяти – и треугольной формы (спереди и сзади, соответственно).

Для китайцев велосипед – главный вид транспорта, популярностью затмевающий автомобили. Но велосипед с угловатыми колесами средством передвижения не станет. По словам изобретателя, поездка на нем требует больше усилий, чем на обычном велосипеде, и скорее всего, он найдет свою нишу в качестве экзотической игрушки и более эффективного тренажера.
Впрочем, все, кто пробовал прокатиться на нем, удивляются вовсе не трудности кручения педалей, а неожиданной плавности хода.
Действительно, казалось бы, угловатые колеса неизбежно должны создавать при качении существенную тряску – но ее Гуаню Байхуа удалось снизить благодаря прекрасному знанию геометрии и настоящей китайской хитрости.
Попробуем доказать это на опыте.
Практическая работа
Цель: проверка возможности движения с помощью колес в форме треугольника Рёло, определение условий для движения без колебаний.
Оборудование: собранные модели, стакан с водой.
Средство передвижения с колесами в форме треугольника Рёло создать реально. Движение осуществлять на таких колесах также возможно, но оно будет недостаточно комфортным. Собственно кататься на этих треугольниках можно только в том случае, если вы перекатываетесь на них, а не используете в качестве колес с осью.
Области применения треугольника Рёло
Но кто бы ни был первооткрывателем этого треугольника, он получил широкое распространение в современном мире. А именно:
- Сверло Уаттса. В 1914 году английский инженер Гарри Джеймс Уаттс изобрел инструмент для сверления квадратных отверстий. Сверло Уаттса представляет собой просто-напросто треугольник Рёло, в котором прорезаны углубления для отвода стружки и заточены режущие кромки





Сверло, деталь патрона и весь патрон Уаттса в сборе
- Двигатель Ванкеля. В 1957 году немецкий изобретатель Ф. Ванкель создал уникальный механизм, где внутри камеры цилиндрической формы по сложной траектории передвигается ротор-поршень, созданный в форме треугольника Рёло. При его постоянном движении каждая его грань, контактируя со стенками камеры, образует сразу три камеры, названные позже «камерами сгорания».
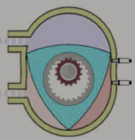

Двигатель Ванкеля позволяет осуществить любой четырёхтактный термодинамический цикл без применения механизма газораспределения. Смесеобразование, зажигание, смазка, охлаждение и пуск в нём принципиально такие же, как у обычных поршневых двигателей внутреннего сгорания. Впервые на серийных автомобилях этот двигатель стала устанавливать компания Mazda. Он установлен на моделях MazdaRX-7 и MazdaRX-8. Поиск альтернативных видов топлива для автомобилей заставил вновь обратить внимание на роторно-поршневой двигатель Ванкеля. Разработчики Mazda уверяют, что по природе своей роторно-поршневой агрегат гораздо лучше приспособлен для работы на водороде, нежели традиционные моторы. Впрочем, по прогнозам специалистов, уже к 2025 году более четверти мирового автопарка будет использовать в качестве топлива водород. Так что возможно, будущее за роторно-поршневыми двигателями.

- Грейферный механизм кинопроекторов. В данном случае треугольник Рёло находится внутри квадрата и двигает рамку, посредством вращения вокруг одного из своих углов. Зуб, который находиться на рамке, входит в перфорацию киноплёнки, протаскивает её на один кадр вниз и выходит обратно. Двигатели дают равномерное вращение оси, а чтобы на экране было четкое изображение, пленку мимо объектива надо протянуть на один кадр, дать ей постоять, потом опять резко протянуть и так 18 раз в секунду. Именно эту задачу решает грейферный механизм.

- Крышки для люков. В форме треугольника Рёло можно изготавливать крышки для люков — опытным путем доказано, что благодаря постоянной ширине они не могут провалиться в люк. Попробуем подвигать крышки люков. Выбираем модель с квадратной крышкой. Крышка проваливается, так как сторона квадрата короче диагонали. Треугольник и трапеция тоже проваливаются. Круг и треугольник Рёло – нет.

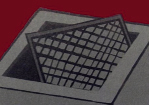
В Сан-Франциско, для системы рекуперирования воды корпуса люков имеют форму треугольника Рёло. За счет того, что у него площадь меньше, чем у круга, себестоимость люков в форме треугольников Рёло была бы ниже, чем у традиционно круглых.

- В качестве кулачка треугольник Рёло использовали немецкие часовые мастера в механизме наручных часов A. Lange & Sohne «Lange 31»
- Форма треугольника Рёло используется и в архитектурных целях. Конструкция из двух его дуг образует характерную для готического стиля стрельчатую арку, однако целиком он встречается в готических сооружениях довольно редко. Окна в форме треугольника Рёло можно обнаружить в церкви Богоматери в Брюгге, а так же в шотландской церкви в Аделаиде. Как элемент орнамента он встречается на оконных решетках аббатства в швейцарской коммуне Отрив.



- Треугольник Рёло используют и в архитектуре, не принадлежащей к готическому стилю. Например, построенная в 2006 году в Кёльне 103-метровая башня под названием «Кёльнский треугольник» в сечении представляет собой именно эту фигуру.

- Треугольник Рёло используется в изготовлении монет. Так уже не один, а несколько, объединенных в семиугольник. Форма таких многоугольников используется в монетном деле: монеты ряда стран. Монета с Бермудских островов в форме треугольника Рёло и старинная английская монета в форме семиугольника Рёло.


- В научно-фантастическом рассказе Пола Андерсона «Треугольное колесо» экипаж землян совершил аварийную посадку на планете, население которой не использовало колёса, так как всё круглое находилось под религиозным запретом. В сотнях километров от места посадки предыдущая земная экспедиция оставила склад с запасными частями, но перенести оттуда необходимый для корабля двухтонный атомный генератор без каких-либо механизмов было невозможно. В итоге землянам удалось соблюсти табу и перевезти генератор, используя катки с сечением в виде треугольника Рёло.
Ход эксперимента
|
№ |
План проведения опыта |
Демонстрация этапа |
Результаты |
Выводы |
|
1. |
Сборка моделей |
|
Модели готовы |
Приступаем к эксперименту. |
|
2. |
Поместим на колеса модели лист фанеры. Установим на платформу стакан с водой Приведем модель в движение. |
|
Вода в стакане колеблется, но не выплескивается |
Лист фанеры и поверхность стола являются опорными прямыми для треугольников Рёло. Расстояние между ними равно ширине колеса, поэтому лист фанеры движется с минимальными колебаниями. |
|
3. |
Рассмотрим модель, у которой колеса имеют форму треугольника Рёло. Приведем модель в движение. |
|
Во время вращения ось поднимается то вверх, то вниз |
Центр колеса описывает сложную фигуру, состоящую из четырех дуг эллипса. Расстояние от центра треугольника до поверхности стола меняется, модель двигается неравномерно. |
Заключение
Таким образом, изобретенный в прошлом веке треугольник Рёло широко используется сегодня. Однако его изучение не стоит на месте. Его свойства как характеристики фигуры постоянной ширины находятся в постоянном теоретическом и практическом изучении. И это правильно, ведь чем лучше будут изучены свойства треугольника Рёло, тем больше возможностей будет открываться для их использования в нашей жизни.
В ходе работы:
– дали определение кривой постоянной ширины и научились строить треугольник Рёло;
– рассмотрели свойства треугольника Рёло, некоторые из них доказали;
– нашли различные практические применение треугольника Рёло в технике, архитектуре и дизайне;
– провели эксперимент по проверке возможности передвижения с помощью колес в форме треугольника Рёло. Эксперимент подтвердил нашу гипотезу: передвижение возможно, но наиболее эффективно использовать треугольник Рёло для формы катков;
Практическая значимость моего исследования заключается в том, что результаты могут найти применение на занятиях по математике; удивительные свойства треугольника Рёло позволяют сделать новые открытия в разных областях жизнедеятельности человека: механике, искусстве и др.
Применение треугольника Рёло используется с давних времен, в настоящее время и будет использоваться в будущем.
Обобщённый материал данного исследования можно применять как на уроках математики, так и во внеурочное время для привития интереса к математике. Данный материал способствует формированию представления о прикладных возможностях математики.
Библиографическая ссылка
Баржанов Б.Р. МОГУТ ЛИ КОЛЕСА БЫТЬ НЕКРУГЛЫМИ // Международный школьный научный вестник. 2018. № 2. ;URL: https://school-herald.ru/ru/article/view?id=482 (дата обращения: 12.03.2026).







