Цель работы – исследовать розы (кривые) Гвидо Гранди.
Кроме привычной для нас прямоугольной декартовой системы координат, в математике используются и другие способы задания положения точки в пространстве или на плоскости. Чаще всего применяются полярные координаты. Положение точки определяется при помощи луча, выходящего из полюса и пересекающего в заданном месте соответствующую окружность. В такие координаты очень естественно укладываются многие природные формы и биологические объекты. Их формы порой самым удивительным образом напоминают фигуры, образуемые в криволинейных координатах достаточно простыми и лаконичными математическими выражениями. Это сходство указывает на то, что тела живых организмов, биологические структуры, образуются по принципам, сходным с принципами построения «полярных» объектов. Живой организм «начинается» из одной исходной точки, и затем развивается и растет во все стороны по определенному математическому закону. По крайней мере, такое предположение совсем не противоречит наблюдаемому в природе обилию «математических», «полярных» форм. Природа как бы сама использует полярные координаты, что особенно бросается в глаза на примере растений, многоклеточных животных и насекомых. Вероятно поэтому фигуры, построенные в полярных координатах, обладают неповторимой эстетической привлекательностью. Они плотно ассоциируются с формами цветов, бабочек, словом, всем тем, что так много удовольствия доставляет нашему взору в живой природе [1].
Полярная система координат. В полярной системе координат положение точки определяется полярным радиусом R и углом φ, образуемым полярным радиусом с полярной осью. Следовательно, полярная система координат – система координат, ставящая в соответствие каждой точке на плоскости пару чисел (R; φ). Основными понятиями этой системы являются точка отсчёта (полюс) и луч, начинающийся в этой точке (полярная ось).
Если в декартовой системе координат предельно простое выражение y = kx определяет прямую линию, то это же выражение, переписанное в форме R = k•φ, уже превращается в спираль. Фигуры в полярных координатах образуются как след конца бегающего по кругу полярного радиуса переменной длины. Длина полярного радиуса определяется величиной угла, который в данный момент времени он образует с полярной осью. Координата φ берётся со знаком « + », если угол от оси до отрезка вычисляется против часовой стрелки, и со знаком «-» в противоположном случае. Любая точка в этой системе имеет бесконечное число координат вида (r; φ + 2πn), которым соответствует одна и та же точка при любых натуральных n. Для полюса r = 0, угол φ произвольный [2].
Связь между полярной и декартовой системами координат. Точка О – полярный полюс, луч ОЕ будем называть полярной осью, отрезок ОМ – называют длиной полярного радиуса R, положительный угол от луча ОЕ до луча F – полярный угол.
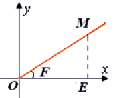
Если известны полярные координаты R и φ, точки М, то можно уставить связь с её декартовыми координатами. Построим прямоугольный ΔОМЕ. В этом треугольнике гипотенуза ОМ = R, 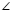 ЕОМ = φ, катет ЕМ = у, катет ОЕ = х координаты точки М. Для того, чтобы перейти от полярных координат к декартовой системе, используют формулы:
ЕОМ = φ, катет ЕМ = у, катет ОЕ = х координаты точки М. Для того, чтобы перейти от полярных координат к декартовой системе, используют формулы: 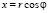 ,
, 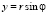 ,
, 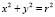 . Обратно, чтобы, имея прямоугольные координаты, получить расстояние нужное для задания полярных координат, надо воспользоваться теоремой Пифагора:
. Обратно, чтобы, имея прямоугольные координаты, получить расстояние нужное для задания полярных координат, надо воспользоваться теоремой Пифагора: 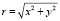 , затем
, затем 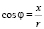 ,
, 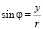 [9]. Построение кривых, заданных полярными уравнениями, имеет некоторые специфические особенности, которые мы проиллюстрируем на примерах. Как известно, математики Древней Индии заменяли доказательства теорем геометрическим чертежом, сопровождая его короткой подписью: «Смотри!». Мы пользовались тем же принципом, заменив долгие разъяснения рисунками, из которых видны все свойства кривых.
[9]. Построение кривых, заданных полярными уравнениями, имеет некоторые специфические особенности, которые мы проиллюстрируем на примерах. Как известно, математики Древней Индии заменяли доказательства теорем геометрическим чертежом, сопровождая его короткой подписью: «Смотри!». Мы пользовались тем же принципом, заменив долгие разъяснения рисунками, из которых видны все свойства кривых.
Классификация плоских кривых
Кривая линия – это множество точек пространства, координаты которых являются функциями одной переменной. Термин «кривая» в разных разделах математики определяется по-разному. Например, (рис. 1) циклоида – траектория движения точки окружности, катящейся без скольжения по прямой линии. Эта кривая состоит их ряда «арок», каждая из которых соответствует полному обороту окружности.
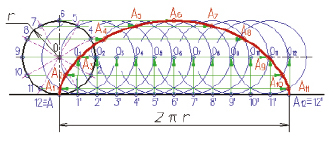
Рис. 1. Циклоида
Каждая кривая включает в себя геометрические элементы, которые составляют её определитель, т.е. совокупность независимых условий, однозначно определяющих эту кривую. Различны и способы задания кривых:
– аналитический – кривая задана математическим уравнением;
– графический – кривая задана визуально на носителе графической информации;· табличный – кривая задана координатами последовательного ряда точек.
Уравнением кривой линии называется такое соотношение между переменными, которому удовлетворяют координаты точки, принадлежащей кривой [8].
В основу классификации кривых положена природа их уравнений.
Кривые подразделяются на алгебраические и трансцендентные в зависимости от того, являются ли их уравнения алгебраическими или трансцендентными в прямоугольной системе координат.Плоская кривая линия называется алгебраической, если её уравнение f (xy) = 0. Функция f (xy) является степенным множителем относительно переменных х и у; в остальных случаях кривая называется трансцендентной. Кривая линия, представленная в декартовых координатах уравнением п-й степени, называется алгебраической кривой п-го порядка. Кривые линии, все точки которых принадлежат одной плоскости, называются плоскими, остальные пространственными [7].
Плоские Кривые линии
Кривые линии, все точки которых принадлежат одной плоскости, называются плоскими.
Порядок плоской алгебраической кривой линии определяется наибольшим числом точек её пересечения прямой линией. Любая прямая линия может пересекать алгебраическую кривую линию п-го порядка не более, чем в п точках.
Рассмотрим несколько примеров алгебраической кривой линии:
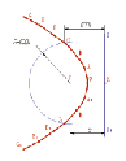
Рис. 2. Парабола
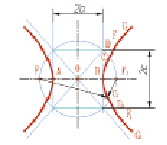
Рис. 3. Гипербола
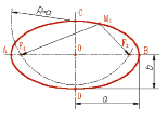
Рис. 4. Эллипс
1. Парабола – кривая второго порядка, прямая пересекает ее в двух точках (рис. 2). При этом парабола может быть определена как:
– множество точек М(A,B,C,...) плоскости, расстояние которых до определенной точки F этой плоскости (фокуса параболы) равно расстоянию до определенной прямой DD1 – директрисы параболы;
– линия пересечения прямого кругового конуса плоскостью, не проходящей через вершину конуса и параллельная какой либо касательной плоскости этого конуса;
– в прямоугольной системе координат 0ху с началом в вершине параболы и осью 0х направленной по оси параболы уравнение параболы имеет так называемый канонический вид
y2 = 2px,
где р (фокальный параметр) – расстояние от фокуса до директрисы.
2. Гипербола:
– множество точек М(A,B,C,...) плоскости, (рис.3) разность (по абсолютной величине) расстояний которых до двух определенных точек F и F1 этой плоскости (фокусов гиперболы) величина постоянная:
FM – F1M = 2а < 2с.
Середина 0 отрезка FF1 (фокусного расстояния) называется центром гиперболы;
– линия пересечения прямого кругового конуса плоскостью, не проходящей через вершину конуса и пересекающая обе его полости;
– в прямоугольной системе координат 0ху с началом в центре гиперболы, на оси 0х которой лежат фокусы гиперболы уравнение гиперболы имеет так называемый канонический вид
х2/а2 – у2/b2 = 1, b2 = с2 – а2,
где а и b длины полуосей гиперболы.
3. Эллипс – множество точек М(xy) плоскости (рис. 4), сумма расстояний МF1 и МF2 которых до двух определенных точек F1 и F2 (фокусов эллипса) постоянна МF1 + МF2 = 2а.
Середина 0 отрезка F1F2 (фокусного расстояния) называется центром эллипса;
– линия пересечения прямого кругового конуса плоскостью, не проходящей через вершину конуса и пересекающей все прямолинейные образующие одной полости этого конуса;
– в прямоугольной системе координат 0ху с началом в центре эллипса, на оси 0х которой лежат фокусы эллипса уравнение эллипса имеет следующий вид:
х2/а2 + у2/b2 = 1,
где а и b – длины большой и малой полуосей эллипса. При а = b фокусы F1 и F2 совпадают и указанное уравнение определяет окружность, которая рассматривается как частный случай эллипса.
Все, рассмотренные выше, плоские кривые линии можно получить как линии пересечения поверхности прямого кругового конуса с плоскостями, различно расположенными по отношению к оси конуса. Поэтому эти кривые называют кривыми конических сечений [6].
Трансцендентные кривые в отличие от алгебраических могут иметь бесконечное количество точек пересечения с прямой, точек перегиба, вершин и т.п. Синусоида – трансцендентная плоская кривая линия (рис. 5), получающаяся в результате двойного равномерного движения точки – поступательного и возвратно-поступательного в направлении, перпендикулярном первому.
Синусоида – график функции у = sin x, непрерывная кривая линия с периодом Т = 2п. Наряду с этим у трансцендентных кривых могут быть характерные точки, которых не существует у алгебраических кривых: точки прекращения, угловые точки (точки излома), асимптотические точки. Простейшими примерами трансцендентных кривых служат графики функций логарифмической, показательной тригонометрической, а также все спирали, циклоиды и т.п.
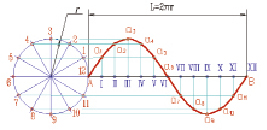
Рис. 5. Синусоида
Розы Гвидо Гранди. Общие свойства
Впервые исследованием роз занимался итальянский геометр Гвидо Гранди. Полная теория этих кривых была изложена им в сочинении «Flores geometrici ex rhodanearum et claelarum deskriptione resultants», изданном в 1728 году [3].
Задача. Отрезок длины 2а движется так, что его концы все время находятся на координатных осях. Составить уравнение траектории основания М перпендикуляра, опущенного из начала координат на отрезок.
Решением данной задачи будет уравнение так называемой четырехлепестковой розы r = a sin 2φ или 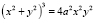 . В полярных координатах общее уравнение для роз записывается в виде: r = a sin kφ или в виде r = a cos kφ, где a и k – положительные числа.
. В полярных координатах общее уравнение для роз записывается в виде: r = a sin kφ или в виде r = a cos kφ, где a и k – положительные числа.
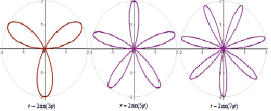
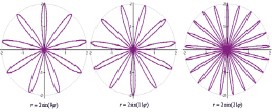
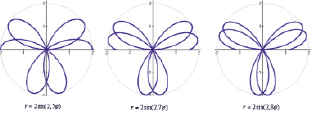
Разнообразие роз Гвидо Гранди
Обратимся к исследованию формы роз. Розы – плоские кривые, уравнения которых в полярных координатах имеют вид
ρ = a sin kφ,
где а и k – постоянные. Если k = m/n – число рациональное, то Р – алгебраич. кривая четного порядка.
Общие свойства:
1. Если k – нечетное число, роза состоит из k лепестков.
2. Если k – четное число, роза состоит из 2k лепестков.
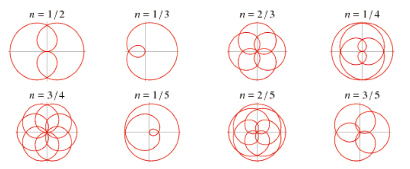
3. Если k = m/n, n > 1, – рациональное число, роза состоит из m лепестков при m и n нечетных и из 2m лепестков, если одно из этих чисел четное (при этом каждый следующий лепесток частично покрывает предыдущий).
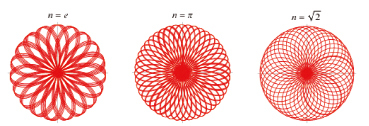
4. Если k – иррациональное число, роза состоит из бесчисленного множества лепестков, частично накладывающихся друг на друга (приложение № 2).
Исследования Хабенихта
Математическим исследованием формы цветов и листьев занимался также Хабенихт – геометр 19 столетия. Им был получен целый ряд уравнений, которые с весьма хорошим приближением выражали аналитически формы листьев клена, щавеля, ивы и т.д. Вот некоторые из этих кривых:в полярных координатах можно описать при помощи косинусов кратных дуг линии, которые обрисовывают контуры листьев некоторых растений:
- кувшинки:
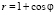 (рис. а);
(рис. а); - кислицы:
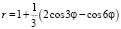 (рис. б);
(рис. б); - настурции:
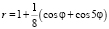 (рис. в);
(рис. в); - стрелолиста:
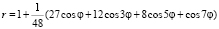 (рис. г).
(рис. г).
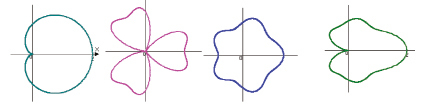
Интересные «цветы» получаются при построении кривых заданных уравнением: 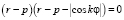 , которое задает на плоскости две линии: окружность r = p и розу
, которое задает на плоскости две линии: окружность r = p и розу 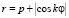 .
.
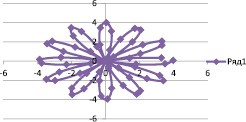
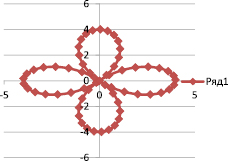
Исследование формы кривой при постоянном значении радиуса r = 2, и изменяющемся значения коэффициента при угле φ [5].
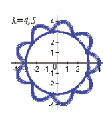
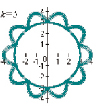
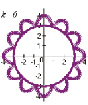
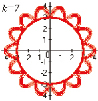
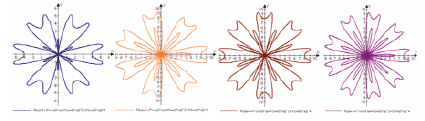
«Цветочная фантазия» на основе кривых Хабенихта, (получены с помощью графопостроителя Advanced Grapher).
Применение
Розы Гранди нашли свое применение в технике, в частности, если некоторая точка совершает колебание вдоль прямой, вращающейся с постоянной скоростью вокруг неподвижной точки – центра колебаний, то траектория этой точки будет розой. Вообще, если k – натуральное число, то роза состоит из 2k лепестков при четном k и из k: лепестков при k нечетном. Если k – рациональное число 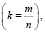 то роза состоит из т лепестков в случае, когда оба числа т и п нечетные, и из 2т лепестков, когда одно из этих чисел является четным; при этом лепестки частично перекрываются. Если k – иррациональное число, то роза состоит из бесконечного множества частично перекрывающихся лепестков.
то роза состоит из т лепестков в случае, когда оба числа т и п нечетные, и из 2т лепестков, когда одно из этих чисел является четным; при этом лепестки частично перекрываются. Если k – иррациональное число, то роза состоит из бесконечного множества частично перекрывающихся лепестков.
Заключение
В данной работе было приведена классификация роз Гвидо Гранди и описаны их основные свойства: порядок алгебраической линии; рассмотрены особые точки кривой; приведена формулы по вычислению длины дуги, радиуса кривизны. Кривая применяется при нарезке зубчатых передач и при описании движения галактических объектов относительно произвольной точки галактики (Земля).
Приложение 1
Инструкция по построению кривых с помощью программы Microsoft Excel [4].
Если уравнение задано в декартовых координатах, то следует перевести его в полярные, используя формулы: X = R*COS(F), Y = R*SIN(F). Следовательно, математическая модель у нас уже есть. Рассмотрим пример построения кривой. Задача. Построить кривую, заданную уравнением 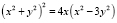 . Решение. Найдем уравнение данной линии в полярных координатах.
. Решение. Найдем уравнение данной линии в полярных координатах.
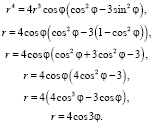
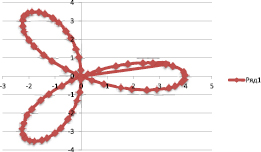
Для программы Microsoft Excel: R = 4*COS(3*F). Предположим, что угол F изменяется в интервалах от 0 до 2?. Для того, чтобы построить эту кривую наиболее точно, с малым шагом изменения угла F, как мы это делали при построении тригонометрических функций, мы выберем шаг изменения 0,1. Построим компьютерную модель исследования. Формулы будут записаны в терминах электронных таблиц следующим образом:
А2 0,1
А3 = А2 + 0,1
B2 = 4*COS(3*F)
C2 = SIN(А2)
D2 = COS(А2)
E2 = B2*D2
F2 = В2*C2
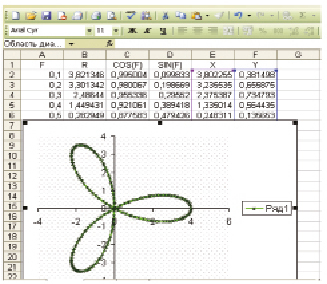
Тогда получаем следующее распределение по столбцам электронной таблицы.
Для построения графика выделим информационный блок E2..F63, так как аргумент F, будем изменять от 0,1 до 6,3 радиана. Возможно изменение и до 9,42, 12,56, и т.д. Получим следующий график.
|
1 |
F |
R |
SIN(F) |
COS(F) |
X |
Y |
|
2 |
0,1 |
3,821346 |
0,099833 |
0,995004 |
3,802255 |
0,381498 |
|
3 |
0,2 |
3,301342 |
0,198669 |
0,980067 |
3,235535 |
0,655875 |
|
4 |
0,3 |
2,48644 |
0,29552 |
0,955336 |
2,375387 |
0,734793 |
|
5 |
0,4 |
1,449431 |
0,389418 |
0,921061 |
1,335014 |
0,564435 |
|
6 |
0,5 |
0,282949 |
0,479426 |
0,877583 |
0,248311 |
0,135653 |
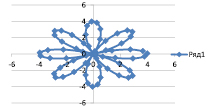
Приложение 2
Мои построения
|
F |
R |
SIN(F) |
COS(F) |
X |
Y |
|
0,1 |
3,684244 |
0,099833 |
0,995004 |
3,665838 |
0,367811 |
|
0,2 |
2,786827 |
0,198669 |
0,980067 |
2,731276 |
0,553657 |
|
0,3 |
1,449431 |
0,29552 |
0,955336 |
1,384694 |
0,428336 |
|
0,4 |
-0,1168 |
0,389418 |
0,921061 |
-0,10758 |
-0,04548 |
|
0,5 |
-1,66459 |
0,479426 |
0,877583 |
-1,46081 |
-0,79805 |
|
0,6 |
-2,94957 |
0,564642 |
0,825336 |
-2,43439 |
-1,66546 |
|
0,7 |
-3,76889 |
0,644218 |
0,764842 |
-2,88261 |
-2,42799 |
|
0,8 |
-3,99318 |
0,717356 |
0,696707 |
-2,78207 |
-2,86453 |
|
0,9 |
-3,58703 |
0,783327 |
0,62161 |
-2,22974 |
-2,80982 |
|
1 |
-2,61457 |
0,841471 |
0,540302 |
-1,41266 |
-2,20009 |
|
1,1 |
-1,22933 |
0,891207 |
0,453596 |
-0,55762 |
-1,09559 |
|
1,2 |
0,349996 |
0,932039 |
0,362358 |
0,126824 |
0,32621 |
|
1,3 |
1,874067 |
0,963558 |
0,267499 |
0,501311 |
1,805772 |
|
1,4 |
3,102264 |
0,98545 |
0,169967 |
0,527283 |
3,057125 |
|
1,5 |
3,840681 |
0,997495 |
0,070737 |
0,271679 |
3,83106 |
|
F |
R |
SIN(F) |
COS(F) |
X |
Y |
|
0,1 |
3,301342 |
0,099833 |
0,995004 |
3,284849 |
0,329584 |
|
0,2 |
1,449431 |
0,198669 |
0,980067 |
1,420539 |
0,287957 |
|
0,3 |
-0,90881 |
0,29552 |
0,955336 |
-0,86822 |
-0,26857 |
|
0,4 |
-2,94957 |
0,389418 |
0,921061 |
-2,71674 |
-1,14862 |
|
0,5 |
-3,95997 |
0,479426 |
0,877583 |
-3,4752 |
-1,89851 |
|
0,6 |
-3,58703 |
0,564642 |
0,825336 |
-2,96051 |
-2,02539 |
|
0,7 |
-1,96104 |
0,644218 |
0,764842 |
-1,49989 |
-1,26334 |
|
0,8 |
0,349996 |
0,717356 |
0,696707 |
0,243845 |
0,251072 |
|
0,9 |
2,538772 |
0,783327 |
0,62161 |
1,578126 |
1,988688 |
|
1 |
3,840681 |
0,841471 |
0,540302 |
2,075129 |
3,231822 |
|
1,1 |
3,80093 |
0,891207 |
0,453596 |
1,724087 |
3,387417 |
|
1,2 |
2,433405 |
0,932039 |
0,362358 |
0,881763 |
2,268029 |
|
1,3 |
0,215822 |
0,963558 |
0,267499 |
0,057732 |
0,207957 |
|
1,4 |
-2,07715 |
0,98545 |
0,169967 |
-0,35305 |
-2,04693 |
|
1,5 |
-3,64452 |
0,997495 |
0,070737 |
-0,2578 |
-3,63539 |
|
F |
R |
SIN(F) |
COS(F) |
X |
Y |
|
0,1 |
3,920266 |
0,099833 |
0,995004 |
3,900681 |
0,391374 |
|
0,2 |
3,684244 |
0,198669 |
0,980067 |
3,610804 |
0,731946 |
|
0,3 |
3,301342 |
0,29552 |
0,955336 |
3,153893 |
0,975613 |
|
0,4 |
2,786827 |
0,389418 |
0,921061 |
2,566837 |
1,085241 |
|
0,5 |
2,161209 |
0,479426 |
0,877583 |
1,89664 |
1,036139 |
|
0,6 |
1,449431 |
0,564642 |
0,825336 |
1,196267 |
0,81841 |
|
0,7 |
0,679869 |
0,644218 |
0,764842 |
0,519992 |
0,437983 |
|
0,8 |
-0,1168 |
0,717356 |
0,696707 |
-0,08137 |
-0,08379 |
|
0,9 |
-0,90881 |
0,783327 |
0,62161 |
-0,56492 |
-0,71189 |
|
1 |
-1,66459 |
0,841471 |
0,540302 |
-0,89938 |
-1,4007 |
|
1,1 |
-2,354 |
0,891207 |
0,453596 |
-1,06777 |
-2,09791 |
|
1,2 |
-2,94957 |
0,932039 |
0,362358 |
-1,0688 |
-2,74912 |
|
1,3 |
-3,42756 |
0,963558 |
0,267499 |
-0,91687 |
-3,30265 |
|
1,4 |
-3,76889 |
0,98545 |
0,169967 |
-0,64059 |
-3,71405 |
|
1,5 |
-3,95997 |
0,997495 |
0,070737 |
-0,28012 |
-3,95005 |
|
F |
R |
SIN(F) |
COS(F) |
X |
Y |
|
0,1 |
0 |
0,099833 |
0,995004 |
0 |
0 |
|
0,2 |
3,301342 |
0,198669 |
0,980067 |
3,235535 |
0,655875 |
|
0,3 |
2,48644 |
0,29552 |
0,955336 |
2,375387 |
0,734793 |
|
0,4 |
1,449431 |
0,389418 |
0,921061 |
1,335014 |
0,564435 |
|
0,5 |
0,282949 |
0,479426 |
0,877583 |
0,248311 |
0,135653 |
|
0,6 |
-0,90881 |
0,564642 |
0,825336 |
-0,75007 |
-0,51315 |
|
0,7 |
-2,01938 |
0,644218 |
0,764842 |
-1,54451 |
-1,30092 |
|
0,8 |
-2,94957 |
0,717356 |
0,696707 |
-2,05499 |
-2,1159 |
|
0,9 |
-3,61629 |
0,783327 |
0,62161 |
-2,24792 |
-2,83274 |
|
1 |
-3,95997 |
0,841471 |
0,540302 |
-2,13958 |
-3,3322 |
|
1,1 |
-3,94992 |
0,891207 |
0,453596 |
-1,79167 |
-3,5202 |
|
1,2 |
-3,58703 |
0,932039 |
0,362358 |
-1,29979 |
-3,34326 |
|
1,3 |
-2,90373 |
0,963558 |
0,267499 |
-0,77674 |
-2,79791 |
|
1,4 |
-1,96104 |
0,98545 |
0,169967 |
-0,33331 |
-1,93251 |
|
1,5 |
-0,84318 |
0,997495 |
0,070737 |
-0,05964 |
-0,84107 |
|
1,6 |
0,349996 |
0,999574 |
-0,0292 |
-0,01022 |
0,349847 |
|
1,7 |
1,511911 |
0,991665 |
-0,12884 |
-0,1948 |
1,499309 |
|
1,8 |
2,538772 |
0,973848 |
-0,2272 |
-0,57681 |
2,472377 |
|
1,9 |
3,338851 |
0,9463 |
-0,32329 |
-1,07942 |
3,159555 |
Библиографическая ссылка
Лавров Г.О. ЗАМЕЧАТЕЛЬНЫЕ КРИВЫЕ: РОЗЫ ГВИДО // Международный школьный научный вестник. 2018. № 3-1. ;URL: https://school-herald.ru/ru/article/view?id=503 (дата обращения: 26.02.2026).
