В данной работе представлен актуальный материал по проектированию проводных компьютерных сетей с использованием теории графов. Рассмотрен один из способов определения минимальных маршрутов кабелей между зданиями.
Для написания реферативной работы по данной теме была подобрана дополнительная учебная литература и интернет-ресурсы.
Цель работы: получить дополнительные знания по современным проводным компьютерным сетям и научиться разрабатывать проекты на объектно-ориентированном языке Delphi (описание формальной модели, разработка графического интерфейса, создание событийных процедур и проведение компьютерного эксперимента с использованием функции генерации случайных чисел).
Задачи: подобрать соответствующий материал с последующей систематизацией, обобщением, иллюстрацией текста и разработкой проекта.
Описательная часть
Компьютерные сети
Описание и определение
После того, как человечеством были созданы персональные компьютеры, потребовалось создание нового подхода к вопросам организации систем, обрабатывающим данные, а также создание новых технологий в сфере хранения, передачи и использования информации. Несколько позже возникла потребность перейти от использования отдельных вычислительных машин, функционирующих в системах, обрабатывающих данные централизовано к системам, способным обрабатывать данные распределенно. Данному перечню потребностей соответствуют компьютерные сети.
Компьютерной сетью называется совокупность компьютеров, которые соединены между собой каналами связи, что позволяет создать единую систему, полностью удовлетворяющей требованиям, предъявляемым правилами распределенной обработки информации. Таким образом, главное назначение компьютерных сетей – это совместная обработка данных, в которой участвуют все компоненты системы, независимо от их физического местоположения. [4]
Компьютерные сети служат для выполнения следующих задач:
- проведения распределенных вычислений;
- организации доступа при централизованной (серверной) обработке информации;
- общего использования аппаратных ресурсов;
- оперативного поиска и получения данных в корпоративных ресурсах;
- оперативного поиска и получения различной информации в глобальных сетях;
- обмена сообщениями, переписки, передачи информации различных видов и т.д.

Рис. 1. Частичная карта Интернета (сайт www.opte.org/maps)
Создание и эволюция первых компьютерных связей и эксперименты с пакетными сетями начались в 50-х годах прошлого века. Колоссальным толчком в развитии сетей послужило создание SNA (англ. Systems Network Architecture) Системной Сетевой Архитектуры, разработанной компанией IBM в 1974 году – общее описание структуры сетей, а также набора команд и протоколов, которые использовались для передачи информации между программами IBM и оборудованием, создавалось для объединения в глобальные сети мейнфреймов IBM. [3]
Самой известной, пожалуй, компьютерной сетью является Всемирная паутина (англ. World Wide Web) – самая большая сеть передачи данных в мире, количество пользователей которой, по данным к середине 2015 года, составило более 3,3 млрд человек (рис. 1). [3]
Терминология и классификация
Граф (англ. graph) – совокупность непустого множества вершин и наборов пар вершин (связей между вершинами).
Интернет (англ. Internet) – всемирная система объединённых компьютерных сетей для хранения и передачи информации.
Компьютерная сеть или вычислительная сеть (англ. computer network) – система, обеспечивающая обмен данными между вычислительными устройствами (компьютеры, серверы и другое оборудование).
Мейнфрейм (также мэйнфрейм, от англ. mainframe) – большой универсальный высокопроизводительный отказоустойчивый сервер со значительными ресурсами ввода-вывода, большим объёмом оперативной и внешней памяти, предназначенный для использования в критически важных системах с интенсивной пакетной и оперативной транзакционной обработкой. [3]
Классификация компьютерных сетей: физическая, логическая и произвольная.
Физическая топология – отражает распределение компонентов сети в пространстве и способ их соединения между собой. Другими словами, это физическая раскладка компонентов или форма сети. Наиболее часто используемыми топологиями являются: общая шина, кольцевая и звездная топологии (рис. 2). В первом случае все компьютеры подключаются к одной общей шине. Во втором – компьютеры объединяются в кольцо. Такое соединение можно получить из первого варианта, если последний компьютер соединить с первым. При звездообразной топологии все компьютеры соединены с одним специальным устройством, обеспечивающим сетевое взаимодействие – концентратором.
Логическая топология – определяет путь прохождения сигналов от одного компьютера к другому. Логическая топология тесно связана с физической (это не значит, что они повторят друг друга). Также логическая топология определяет адресацию устройств в рамках физической передающей среды.
Произвольная топология, часто называемая сетевой, предполагает наличие многих избыточных соединений между всеми (или почти всеми) компьютерами.
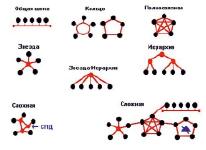
Рис. 2. Представление топологии компьютерных сетей в виде графов
Возможны гибридные топологии на базе трех рассмотренных.
Область действия сети учитывает географический район, охваченный сетью, и, в меньшей степени, размер сети и ее физическую топологию. [11]
Выделяют следующие типы компьютерных сетей:
- локальные (англ. Local Area Network, LAN), развернутые на небольшой площади (комната, этаж, здание, несколько рядом расположенных зданий) (рис. 3);

Рис. 3. Локальная компьютерная сеть
- территориальные (городские, областные и т. п.) – сети, состоящие из некоторого количества локальных сетей (рис. 4);
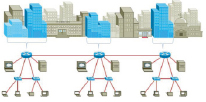
Рис. 4. Территориальная компьютерная сеть
- корпоративные – сети крупных предприятий, содержащие достаточно большое количество локальных сетей, распределенных на большой территории и часто (но не обязательно) использующих для связи между собой глобальные сети, в частности Интернет. В этом случае корпоративные сети – это частные виртуальные сети (рис. 5);

Рис. 5. Корпоративная компьютерная сеть
- глобальные сети (англ. Wide Area Network, WAN) – сети, состоящие из массы локальных сетей и отдельных компьютеров с производительными связями и практически неограниченными территориями (в пределах стран и даже континентов) (рис. 6). [4, 6, 10]

Рис. 6. Глобальная компьютерная сеть
Клиенты сети (англ. network clients) – компьютеры или другие сетевые устройства, например принтеры, имеющие доступ к ресурсам сети.
Узел (англ. node) – точка соединения в сети. В общем случае узел представляет собой точку перераспределения, или устройство, запрограммированное или спроектированное для распознавания и обработки запросов на передачу информации другим узлам. Часто это специально выделенный компьютер.
Хост (англ. host) – основной узловой компьютер или любое устройство, подключенное к сети. Другими словами, хост – это информационный узел сети, который не является маршрутизатором, то есть, не передающий информацию из одной сети в другую.
Маршрутизатор (англ. router) – специализированный сетевой компьютер, имеющий два или более сетевых интерфейсов и пересылающий пакеты данных между различными сегментами сети. Маршрутизатор может связывать разнородные сети различных архитектур.
Протокол (англ. protocol) – правила передачи информации по сети.
Стек (англ. stack) – семейство протоколов: стандартизованный набор протоколов, охватывающий несколько уровней. Раньше фирмы выпускали компьютеры и сетевое оборудование, поддерживающие только свои стеки протоколов, из-за чего возникали проблемы несовместимости. Сейчас все популярные стеки протоколов стали включаться в состав сетевых операционных систем различных производителей. Наиболее распространенные стеки коммуникационных протоколов – TCP/IP, NetBIOS/SMB, IPX/SPX. В настоящее время наблюдается тенденция к сближению протоколов локальных и глобальных сетей. Ярким примером являются протоколы технологии АТМ, работающие без изменений как в тех, так и в других сетях. Однако, большинство протоколов, используемых сегодня, относятся либо к локальным, либо к глобальным сетям. Различия между протоколами локальных и глобальных сетей происходят в основном из-за различий между свойствами каналов, использующихся в этих сетях. Каналы локальных сетей имеют небольшую длину и высокое качество, а каналы глобальных сетей – наоборот, большую длину и низкое качество.
СПД (англ. data network) – сеть передачи данных, или «компьютерная сеть».
Трафик (англ. traffic) – поток данных по каналу связи или через сетевое устройство, а также объем этого потока в байтах. [1]
Технические характеристики
Диаметром сети называется расстояние между двумя наиболее удаленными друг от друга станциями данной сети.
Важнейшая характеристика компьютерной сети – её пропускная способность. Пропускная способность (битовая скорость передачи информации) – это количество информации, которое можно передать по данной сети за единицу времени. Пропускная способность измеряется в бит/с. 1 бит/с равен 1 биту информации, переданному за 1 с. Используются кратные единицы: Кбит/с, Мбит/с, Гбит/с.
В зависимости от характера распределения функций различают:
- одноранговые сети – небольшие локальные сети, в которых все компьютеры являются функционально равноправными; обычно включают в себя до 15 станций;
- сети с выделенными серверами (двухранговые сети) – средние и крупные сети, в которых часть выполняемых функций по обслуживанию станций возложена на серверы. [5]
Защищённость – показывает, насколько защищена сама сеть и данные, передаваемые в ней. Понятие защиты очень важно в компьютерной сети. Защита должна быть продумана перед любым внесением изменений, влияющих на сеть.
Доступность – мера, показывающая, насколько сеть будет доступна для использования при необходимости.
Масштабируемость (расширяемость) – показывает, насколько легко сеть может быть расширена, т.е. сможет обслуживать большее количество пользователей или передавать большее количество данных.
Надёжность – показывает надёжность компонентов (маршрутизаторов, коммутаторов, персональных компьютеров и т.д.), комплектующих сеть и измеряет возможность аварий, называя среднее время между авариями (MTBF – mean time between failure).
Эти характеристики и атрибуты дают возможность сравнивать различные сетевые решения.
Самыми распространёнными сетевыми пользовательскими приложениями являются электронная почта, веб браузер, программы для обмена сообщениями, приложения для совместной разработки проектов и базы данных. [2]
Проектирование компьютерных сетей
При проектировании проводных компьютерных сетей необходимо определить расстояние маршрута прокладки кабеля минимальной длины, но подходящего к каждому зданию. Для решения таких задач наиболее удобно использовать теорию графов (рис. 7).
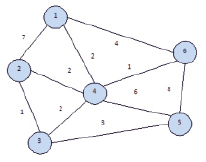
Рис. 7. Прокладка коммуникаций
Теория графов для оптимизации расчётов
Основные понятия теории графов
Объектный граф – это совокупность непустого множества узлов и ребер, соединяющих эти узлы. Объектные графы обеспечивают простой способ учёта взаимных связей во множестве объектов. Является основным объектом изучения математической теории графов, обширного самостоятельного раздела дискретной математики. Используется при проектировании компьютерных сетей, трубопроводов, строительстве дорог для минимизации затрат на прокладку коммуникаций.
Объекты представляются как вершины, или узлы графа, а связи – как дуги, или рёбра. Для разных областей применения виды графов могут различаться направленностью, ограничениями на количество связей и дополнительными данными о вершинах или рёбрах.
Вершины, соединенные ребром, называются смежными. Ребра, имеющие общую вершину, также называются смежными. Ребро и любая из его двух вершин называются инцидентными. Степень вершины – количество инцидентных ей ребер. Каждый граф можно представить на плоскости множеством точек, соответствующих вершинам, которые соединены линиями, соответствующими ребрам.
Графы бывают ориентированными и неориентированными. Ориентированный граф (кратко орграф) – граф, рёбрам которого присвоено направление. Направление ребра именуется дугами, а в некоторых источниках и просто рёбрами (рис. 2). Неориентированным графом называется множество как угодно размещенных на плоскости точек, некоторые из которых соединены линиями любой формы. Два неориентированных графа считаются любой формы. Два неориентированных графа считаются неразличимыми, если они отличаются друг от друга только формой соединительных линий или способом размещения точек на плоскости (рис. 1) . [3, 9]
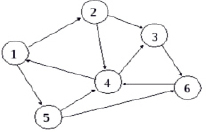
Рис. 1. Пример неориентированного графа
Описание графа с помощью матрицы смежности
Матрица смежности однозначно определяет структуру графа. Примеры ориентированного графа и его матрицы смежности приведены соответственно на рис. 2 и рис. 3. Отметим, что петля в матрице смежности может быть представлена соответствующим единичным диагональным элементом. Кратные ребра можно представить, позволив элементу матрицы быть больше 1, но это не принято, обычно же представляют каждый элемент матрицы одним двоичным разрядом [8].
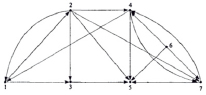
Рис. 2. Ориентированный граф

Рис. 3. Матрица смежности ориентированного графа
Описание графа с помощью дерева
Дерево – это граф, в котором нет циклов, т.е. граф, в котором нельзя из некоторой вершины пройти по нескольким различным рёбрам и вернуться в ту же вершину. Остовным связным деревом называется подграф, включающий все вершины исходного графа, каждая вершина которого достижима на любой другой, и при этом не содержащий циклов. [12]
Проектная часть
Описание формальной модели проекта
Разработаем проект, позволяющий получать остовные связные деревья минимального веса для графов с 5-ю вершинами. Графы в виде схем будем рисовать в графических полях, а матрицы смежности выводить в элемент управления, представляющий собой таблицу. [7,12]
Компьютерная модель проекта
1. Создадим графический интерфейс проекта: (рис. 1)
Поместить на форму:
- графическое поле Image1 для рисования первоначального графа;
- графическое поле Image2 для рисования остовного связного дерева минимального веса;
- кнопку Button1 для запуска событийной процедуры вывода вершин графа в первое графическое поле;
- кнопку Button2 для запуска событийной процедуры вывода элементов матрицы смежности взвешенного ориентированного графа;
- управляющий элемент StringGrid1 для вывода элементов матрицы смежности связного взвешенного ориентированного графа;
- кнопку Button3 для запуска событийной процедуры вывода элементов матрицы смежности взвешенного неориентированного графа;
- управляющий элемент StringGrid2 для вывода элементов матрицы смежности связного взвешенного неориентированного графа;
- кнопку Button4 для запуска событийной процедуры вывода во второе графическое поле остовного связного дерева;
- управляющий элемент StringGrid3 для вывода весов рёбер остовного связного дерева;
- надпись Label1 для вывода суммы весов остовного связного дерева минимального веса;
- надписи для вывода пояснительных текстов. [7,12]
2. Создадим событийные процедуры:
- под кнопкой Button1 – событийную процедуру генерации случайных координат вершин графа и их рисование в графическом поле;
- под кнопкой Button2 – событийную процедуру вывода элементов матрицы смежности взвешенного ориентированного графа (во вложенном цикле со счётчиком n (строки матрицы) и k (столбцы матрицы) осуществим рисование рёбер ориентированного графа, вычисление весов рёбер и их вывод в таблицу);
- под кнопкой Button3 – событийную процедуру вывода элементов матрицы смежности взвешенного неориентированного графа (во вложенном цикле со счётчиком N (строки матрицы) и K (столбцы матрицы) осуществим рисование рёбер неориентированного графа, вычисление весов рёбер и их вывод в таблицу. Для вывода половины элементов матрицы смежности начальному значению счётчика вложенного цикла присвоим значение K=N+1);
- под кнопкой Button4 – событийную процедуру построения остовного связного дерева минимального веса. Ребро минимального веса выбирается с использованием матрицы смежности неориентированного графа. Ввод номеров вершин ребра минимального веса осуществляется с помощью функции ввода данных InputBox(). Включение или невключение выбранного ребра в остовное дерево производится на основании пункта 3 алгоритма Крускала, который реализуется с использованием функции вывода сообщений MessageDlg() и оператора условного перехода в сокращённой форме. В результате остовное связное дерево минимального веса будет нарисовано в графическом поле, веса рёбер будут выведены в таблицу, а суммарный вес рёбер – на надпись. На основе анализа матрицы смежности неориентированного графа выберем ребро минимального веса. [7,12]
Программный код проекта со всеми событийными процедурами на языке Delphi представлен в приложении.
Компьютерный эксперимент
Запустить проект на выполнение:
1. Щелкнуть по кнопке Вершины графа. В графическое поле будут выведены вершины графа и их номера. Для моделирования расположения вершин и выбора наиболее оптимального варианта щёлкнуть несколько раз (рис. 2).

Рис. 1. Графический интерфейс проекта
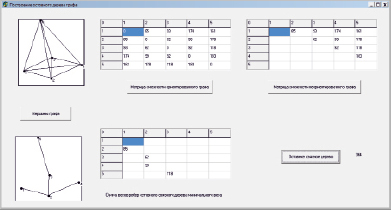
Рис. 2. Поэтапное выполнение проекта в среде Delphi
2. Осуществить щелчок по кнопке Матрица смежности ориентированного графа. В графическом поле будут нарисованы рёбра графов, а в таблицу будут выведены веса рёбер ориентированного графа (рис. 2).
3. Осуществить щелчок по кнопке Матрица смежности неориентированного графа. В таблицу будут выведены веса рёбер неориентированного графа (рис. 2). На основе анализа матрицы выбираем ребро минимального веса (рис. 2).
4. Осуществить щелчок по кнопке Остовное связное дерево. В появившемся диалогом окне Выбор ребра минимального веса ввести номер первой точки и щёлкнуть по кнопке ОК (рис. 2).
5. В появившемся диалогом окне Выбор ребра минимального веса ввести номер второй точки и щёлкнуть по кнопке ОК (рис. 2).
6. В появившемся диалогом окне Confirm подтвердить или опровергнуть истинность о включении выбранного ребра в остовное дерево щелчком по кнопке Yes или No (рис. 2).
7. Выполнять пункты 4 – 6 до тех пор, пока остовное связное дерево с минимальным весом не будет построено, т.е. пока все вершины не войдут в связное множество (рис. 2). [7, 12]
Анализ полученных результатов
В результате:
1. В графическом поле будет построено остовное связное дерево.
2. В соответствующие ячейки таблицы будут выведены веса рёбер остовного дерева.
3. На надпись будет выведена сумма весов рёбер остовного связного дерева минимального веса. [12]
Заключение
Таким образом, при проектировании проводных компьютерных сетей удобно использовать теорию графов. Генерация координат вершин графа случайным образом путём поэтапного анализа даёт возможность найти минимальный вес всех рёбер построенного остовного дерева графа.
Приложение
Программный код проекта
Var //Раздел переменных
X: array[1..5] of integer;
Y: array[1..5] of integer;
R: array[1..5,1..5] of integer;
R1: array[1..5,1..5] of integer;
I, N, K, A: byte;
S: integer;
strN, strK: string;
procedure TForm1.Button1Click(Sender: TObject);
begin
//Очистка областей рисования и обнуление переменной
Image1.Canvas.Brush.Color:=clWhite;
Image1.Canvas.Rectangle(0,0,200,200);
Image2.Canvas.Brush.Color:=clWhite;
Image2.Canvas.Rectangle(0,0,200,200);
S:=0;
//Обозначение строк и столбцов в элементах управления StringGrid
For I:=0 To 6 Do
begin
StringGrid1.Cells[I,0]:=IntToStr(I);
StringGrid1.Cells[0,I]:=IntToStr(I);
StringGrid2.Cells[I,0]:=IntToStr(I);
StringGrid2.Cells[0,I]:=IntToStr(I);
StringGrid3.Cells[I,0]:=IntToStr(I);
StringGrid3.Cells[0,I]:=IntToStr(I);
end;
//Генерация случайных координат вершин графа и их рисование
For I:=1 To 5 Do
begin
X[I]:=Random(200);
Y[I]:=Random(200);
Image1.Canvas.Pen.Width:=3;
Image1.Canvas.Ellipse(X[I],Y[I],X[I]+4,Y[I]+4);
Image1.Canvas.TextOut(X[I]+5,Y[I],IntToStr(I));
end;
end;
procedure TForm1.Button2Click(Sender: TObject);
begin
//Во вложенном цикле рисование рёбер ориентированного
//графа, вычисление весов рёбер и их вывод в таблицу
For N:=1 To 5 Do
begin
For K:=1 To 5 Do
begin
Image1.Canvas.Pen.Width:=1;
Image1.Canvas.MoveTo(X[N], Y[N]);
Image1.Canvas.LineTo(X[K], Y[K]);
R[N,K]:=Round(Sqrt(Sqr(X[N]-X[K])+ Sqr(Y[N]-Y[K])));
StringGrid1.Cells[N,K]:=IntToStr(R[N,K]);
end;end;
end;
procedure TForm1.Button3Click(Sender: TObject);
begin
//Во вложенном цикле вычисление весов рёбер
//неориентированного графа и их вывод в таблицу
For N:=1 To 5 Do
begin
For K:=N+1 To 5 Do
begin
R[N,K]:=Round(Sqrt(Sqr(X[N]-X[K])+ Sqr(Y[N]-Y[K])));
StringGrid2.Cells[K,N]:=IntToStr(R[K,N]);
end;end;
end;
procedure TForm1.Button4Click(Sender: TObject);
begin
//Ввод номера первой вершины и её рисование в графическом поле
strN:=InputBox(‘Выбор ребра мин. веса’, ‘Введите первой вершины:’,’ ‘);
Image2.Canvas.Pen.Width:=3;
Image2.Canvas.Ellipse(X[StrToInt(strN)],Y[StrToInt(strN)],X[StrToInt(strN)]+
4,Y[StrToInt(strN)]+4);
Image2.Canvas.TextOut(X[StrToInt(strN)]+5,Y[StrToInt(strN)],StrN);
//Ввод номера второй вершины и её рисование в графическом поле
strK:=InputBox(‘Выбор ребра минимального веса’, ‘ Введите номер первой вершины:’,’ ‘);
Image2.Canvas.Pen.Width:=3;
Image2.Canvas.Ellipse(X[StrToInt(strK)],Y[StrToInt(strK)],X[StrToInt(strK)]+
4,Y[StrToInt(strK)]+4);
Image2.Canvas.TextOut(X[StrToInt(strK)]+5,Y[StrToInt(strK)],StrK);
//Реализация пункта 3 алгоритма Крускала
A:=MessageDlg(‘Ребро с вершинами ‘ + StrN + ‘ и ‘ + strK +
‘ включить в состав остовного дерева, если выполняется хотя бы одно из условий.’,
MtConfirmation,[mbYes,mbNo], 0);
If A=mrYes
Then
begin
Image2.Canvas.Pen.Width:=1;
Image2.Canvas.MoveTo(X[StrToInt(strN)],Y[StrToInt(strN)]);
Image2.Canvas.LineTo(X[StrToInt(strK)],Y[StrToInt(strK)]);
R1[StrToInt(strN),StrToInt(strK)]:=Round(Sqrt(Sqr(X[StrToInt(strN)]-X[StrToInt(strK)]) +
Sqr(Y[StrToInt(strN)]-Y[StrToInt(strK)])));
//Найти сумму весов рёбер остовного связного дерева минимального веса
S:=S + R1[StrToInt(strN),StrToInt(strK)];
StringGrid3.Cells[StrToInt(strN),StrToInt(strK)]:=IntToStr(R1[StrToInt(strN),
StrToInt(strK)]);
end;
//Вывести значение суммы минимального веса в метку
Label2.Caption:=IntToStr(S);
end;
end.
Библиографическая ссылка
Титов Н.А. ИССЛЕДОВАНИЕ ГРАФОВ ПРИ ПРОЕКТИРОВАНИИ КОМПЬЮТЕРНЫХ СЕТЕЙ НА ЯЗЫКЕ ОБЪЕКТНО-ОРИЕНТИРОВАННОГО ПРОГРАММИРОВАНИЯ DELPHI // Международный школьный научный вестник. 2018. № 1. ;URL: https://school-herald.ru/ru/article/view?id=516 (дата обращения: 12.03.2026).
