Данная статья является реферативным изложением основной работы. Полный текст научной работы, приложения, иллюстрации и иные дополнительные материалы доступны на сайте IV Международного конкурса научно – исследовательских и творческих работ учащихся «Старт в науке» по ссылке: https://school-science.ru/1017/7/770.
Гипотеза, актуальность, цель, задачи проекта, объект и предмет исследований, результаты
Цель: Выявить, доказать малоизвестные теоремы, свойства геометрии.
Задачи исследования:
1. Изучить учебную и справочную литературу.
2. Собрать малоизвестный теоретический материал, необходимый для решения планиметрических задач.
3. Разобраться в доказательствах малоизвестных теорем и свойств.
4. Найти и решить задачи КИМов ЕГЭ, на применение этих малоизвестных теорем и свойств.
Актуальность: В ЕГЭ в заданиях по математике, часто встречаются задачи по геометрии, решение, которых вызывают некоторые затруднения, и заставляют тратить много времени. Умение решать такие задачи является неотъемлемым условием успешной сдачи ЕГЭ профильного уровня по математике. Но есть решение этой проблемы, некоторые из данных задач можно с лёгкостью решить, используя теоремы, свойства, которые являются малоизвестными, и им не уделяется внимание в школьном курсе математики. На мой взгляд, этим можно объяснить мой интерес к теме исследования и её актуальность.
Объект исследования: геометрические задачи КИМов ЕГЭ.
Предмет исследования: малоизвестные теоремы и свойства планиметрии.
Гипотеза: Существуют малоизвестные теоремы и свойства геометрии, знание которых облегчит решение некоторых планиметрических задач КИМов ЕГЭ.
Методы исследования:
1) Теоретический анализ и поиск информации о малоизвестных теоремах и свойствах;
2) Доказательство теорем и свойств
3) Поиск и решение задач с применением данных теорем и свойств
В математике, а в целом в геометрии присутствует огромное количество различных теорем, свойств. Известно много теорем и свойств для решения планиметрических задач, которые актуальны и по сей день, но являются малоизвестными, и очень полезными для решения задач. При изучение данного предмета усваиваются лишь основные, всеми известные теоремы и способы решения геометрических задач. Но помимо этого существует довольно большое количество различных свойств и теорем, которые упрощают решение той, или иной задачи, но мало кто про них знает вообще. В КИМах ЕГЭ решать задачи по геометрии можно в разы проще, зная эти малоизвестные свойства и теоремы. В КИМах задачи по геометрии встречаются в номерах в 8, 13, 15 и 16. Малоизвестные теоремы и свойсва, описанные в моей работе, упрощают в разы решение планиметрических задач.
Теорема о биссектрисе углов треугольника
Теорема: биссектриса угла треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.
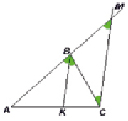
Доказательство.
Рассмотрим треугольник АВС и биссектрису его угла В. Проведем через вершину С прямую СМ, параллельную биссектрисе ВК, до пересечения в точке М продолжением стороны АВ. Так как ВК – биссектриса угла АВС, то ∠АВК = ∠КВС. Далее, ∠АВК = ∠ВМС, как соответственные углы при параллельных прямых, и ∠КВС = ∠ВСМ, как накрест лежащие углы при параллельных прямых. Отсюда ∠ВСМ = ∠ВМС, и поэтому треугольник ВМС – равнобедренный, откуда ВС = ВМ. По теореме о параллельных прямых, пересекающих стороны угла, имеем АК: КС = АВ: ВМ = АВ: ВС, что и требовалось доказать.
Рассмотрим задачи, при решении которых используется свойство биссектрис треугольника.
Задача № 1. В треугольнике ABC биссектриса AH делит сторону BC на отрезки, длины которых равны 28 и 12. Найдите периметр треугольника ABC, если AB – AC = 18.
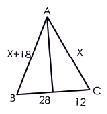
Дано:
AВС – треугольник
АH – биссектриса
BH = 28
HC = 12
Найти: P
Решение:
Пусть AC = X тогда AB = X + 18
По свойству биссектрисы угла альфа, AB·HC = BH·AC;
28·X = 12·(х + 18)х = 13,5,
значит AC = 13,5, откуда
AB = 13,5 + 18 = 31,5BC = 28 + 12 = 40,
тогда
P = AB + BC + AC = 85
Ответ: 8
Теорема о медианах треугольника
Теорема. Медианы треугольника пересекаются в одной точке и делятся в ней в отношении 2:1, считая от вершины.
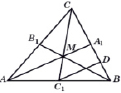
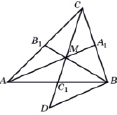
Доказательство. В треугольнике A BC проведем медианы AA1 и CC1 и их точку пересечения обозначим M.
Через точку C1 проведем прямую, параллельную AA1 и ее точку пересечения с BC обозначим D.
Тогда D – середина BA1, следовательно, CA1:A1D = 2:1.
По теореме Фалеса, CM:MC1 = 2:1. Таким образом, медиана AA1 пересекает медиану CC1 в точке M, делящей медиану CC1 в отношении 2:1.
Аналогично, медиана BB1 пересекает медиану CC1 в точке, делящей медиану CC1 в отношении 2:1, т.е. точке M.
Рассмотрим примеры решения задач.
Задача № 1. Докажите, что медиана треугольника лежит ближе к большей стороне, т.е. если в треугольнике ABC, AC>BC, то для медианы CC1 выполняется неравенство ACC1< BCC1.
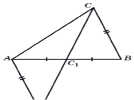
Решение.
Продолжим медиану CC1и отложим отрезок C1B, равный AC1. Треугольник AC1D равен треугольнику BC1C по двум сторонам и углу между ними. Следовательно, AD = BC, ADC1 = BCC1. В треугольнике ACD AC> AD. Так как против большей стороны треугольника лежит больший угол, то ADC1>ACD. Следовательно, выполняется неравенство ACC1<BCC1.
Задача № 2. Площадь треугольника ABC равна 1. Найдите площадь треугольника, стороны которого равны медианам данного треугольника.
Дано:
ABC-треугольник
S = 1
Найти::S2
Решение:
Пусть AA1, BB1, CC1 – медианы треугольника ABC, пересекающиеся в точке M. Продолжим медиану CC1 и отложим отрезок C1D, равный MC1.
Площадь треугольника BMC равна 1/3, и его стороны равны 2/3 медиан исходного треугольника. Следовательно, площадь треугольника, стороны которого равны медианам данного треугольника, равна 3/4.Выведем формулу, выражающую медианы треугольника через его стороны. Пусть стороны треугольника ABC равны a, b, c. Искомую длину медианы CD обозначим mc. По теореме косинусов имеем:
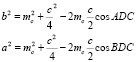
Складывая эти два равенства и учитывая, что cosADC = –cosBDC, получаем равенство: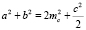 
из которого находим 
.
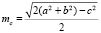Теорема о средних линиях треугольника
Теорема: три средние линии треугольника делят его на 4 равных треугольника, подобных данному с коэффициентом подобия ½
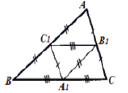
Доказательство:
Пусть ABC – треугольник. С1 – середина АВ, А1 – середина ВС, В1- середина АС.
Докажем, что треугольники AС1В1, BС1А1, А1В1C, С1В1А1 равны.
Так как С1 А1 В1 – середины, то AС1 = С1B, BА1 = А1C, AВ1 = В1C.
Используем свойство среднее линии:
С1А1 = 1/2 ·AC = 1/2 ·(AВ1 + В1C) = 1/2 ·(AВ1 + AВ1) = AВ1
Аналогично С1В1 = А1C, А1В1 = АС1.
Тогда в треугольниках AС1В1, BА1С1, A1В1C, С1В1А1
AС1 = BС1 = А1В1 = А1В1
AВ1 = С1А1 = В1C = C1A1
С1В1 = BА1 = А1C = С1В1
Значит треугольники равны по трем сторонам, из этого следует, что
А1/B1 = A1C1/AC = B1C1/BC = ½
Теорема доказана.
Рассмотрим решение задач с применением свойства средних линий треугольника.
Задача № 1. Дан треугольник АBС со сторонами 9,4 и 7. Найдите периметр треугольника C1A1B1вершинами которого являются середины данных сторон
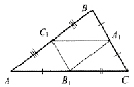
Дано: треугольник – АВС
9,4,7-стороны треугольника
Найти: P
Решение
По свойству подобия треугольников: 3 средние линии треугольника делят его на 4 равные треугольника, подобные данному с коэффициентом 1/2.
C1A1 = 9/2 = 4.5 A1B1 = 4/2 = 2 C1B1 = 7/2 = 3.5 отсюда периметр равен = 4,5 + 2 + 3,5 = 10
Ответ: 10
Свойство касательной к окружности
Теорема: квадрат касательной равен произведению секущей на её внешнюю часть.
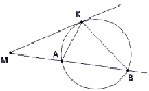
Доказательство.
Проведём отрезки AK и BK.Треугольники AKM и BKM подобны т. к. угол M у них общий. А углы AKM и B равны, так как каждый из них измеряется половиной дуги AK. Следовательно, MK/MA = MB/MK, или MK2 = MA·MB.
Примеры решения задач.
Задача № 1. Из точки А вне окружности проведены секущая, длиной 12 см и касательная, длина которой в 2 раза меньше отрезка секущей, находящегося внутри окружности. найдите длину касательной.
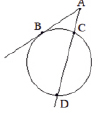
Дано:
AD = 12
ACD-секущая
CD/AB = 2
Найти: AB
Решение:
Если из одной точки проведены к окружности касательная и секущая, то произведение всей секущей на её внешнюю часть равно квадрату касательной,
то есть AD·АC = АB2. ИлиAD·(AD-2АB) = АB2.
Подставляем известные значения: 12(12-2АB) = АB2 или АB2 + 24·АB-144.
АB = -12 + 12v2 = 12(v2-1)
Свойство сторон описанного четырёхугольника
Теорема: у четырёхугольника, описанного около окружности, суммы длин противоположных сторон равны
Доказательство:
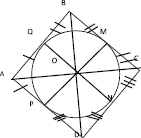
По свойству касательной AP = AQ, DP = DN,CN = CM,и BQ = BM, получаем, что
AB + CD = AQ + BQ + CN + DNиBC + + AD = BM + CM + AP + DP.
Следовательно
AB + CD = BC + AD
Рассмотрим примеры решения задач.
Задача № 1. Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как 1:2:3. Найдите большую сторону этого четырехугольника, если известно, что его периметр равен 32.
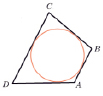
Дано:
ABCD – четырёхугольник
AB:BC:CD = 1:2:3
P = 32
Найти: DC
Решение:
Пусть сторона AB = x, тогда AD = 2х, а DC = 3х. По свойству описанного четырехугольника, суммы противоположных сторон равны, и значит х + 3х = BC + 2х, откуда ВС = 2х, тогда периметр четырехугольника равен 8X.
Получаем, что х = 4, а большая сторона равна 12.
Ответ: 12
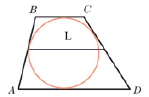
Задача № 2. Около окружности описана трапеция, периметр которой равен 40. Найдите ее среднюю линию.
Дано:
ABCD-трапеция, l – средняя линия
P = 40
Найти: L
Решение: Средняя линия трапеции равна полусумме оснований. Пусть основания трапеции равны a и c, а боковые стороны b и d.По свойству описанного четырехугольника, a + c = b + d, и значит, периметр равен 2(a + c).
Получаем, что а + с = 20, откуда L = 10
Ответ:10
Формула Пика
Теорема Пика: площадь многоугольника равна:
Г:2 + В – 1,
где Г – число узлов решетки на границе многоугольника
В – число узлов решетки внутри многоугольника.
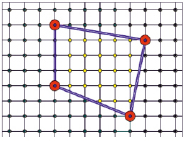
Например, для вычисления площади четырёхугольника, изображённого на рисунке, считаем:
Г = 7, В = 23,
откуда S = 7:2 + 23 – 1 = 25,5.
Площадь любого многоугольника, нарисованного на клетчатой бумаге, легко посчитать, представив её как сумму или разность площадей прямоугольных треугольников и прямоугольников, стороны которых идут по линиям сетки, проходящим через вершины нарисованного треугольника.
В некоторых случаях и вовсе можно применить готовую формулу площади треугольника или четырёхугольника. Но в отдельных случаях данные методы применить либо невозможно, либо процесс их применения является трудоёмким, неудобным.
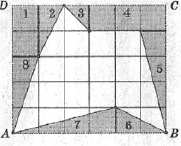
Чтобы вычислить площадь многоугольника, изображенного на рисунке, применяя формулу Пика, имеем: S = 8/2 + 19-1 = 22.
Заключение
В ходе исследований подтвердилась гипотеза о том, что в геометрии существуют малоизвестные из школьного курса теоремы и свойства, которые упрощают решение некоторых планиметрических задач, в том числе и задач КИМов ЕГЭ.
Мне удалось найти такие теоремы и свойства и применить их к решению задач, и доказать, что их применение сводит огромные решения некоторых задач, к решениям за пару минут. Применение описанных в моей работе теорем, свойств в отдельных случаях позволяет решить задачу сходу и устно, и позволяет сохранить больше времени на ЕГЭ и просто при их решение в школе.
Я считаю, что материалы моих исследований могут быть полезны выпускникам при подготовке к сдаче ЕГЭ по математике.
Библиографическая ссылка
Хворов И.И. МАЛОИЗВЕСТНЫЕ ТЕОРЕМЫ ПЛАНИМЕТРИИ // Международный школьный научный вестник. – 2018. – № 3-2. ;URL: https://school-herald.ru/ru/article/view?id=544 (дата обращения: 21.12.2024).