Данная статья является реферативным изложением основной работы. Полный текст научной работы, приложения, иллюстрации и иные дополнительные материалы доступны на сайте IV Международного конкурса научно – исследовательских и творческих работ учащихся «Старт в науке» по ссылке: https://school-science.ru/1017/7/1348.
Пчелы – удивительное творение природы: миллионы лет они строят ячейки сотов правильной шестиугольной формы (были найдены окаменелые останки пчелы возрастом в 100 миллионов лет). Все ячейки имеют совершенно одинаковый размер.
Почему была выбрана именно шестиугольная форма построения ячеек? В процессе выполнения данной работы мы постараемся дать исчерпывающий ответ на поставленный вопрос.
Тема исследования: Математические тайны пчелиной ячейки
Объект исследования: ячейка пчелиных сотов.
Предмет исследования: шестигранная форма ячейки пчелиных сотов.
Цель исследования: математическими методами исследовать строение пчелиной ячейки на вместимость и экономичность.
Задачи исследования:
- Исследование замощения плоскости правильными многоугольниками.
- Исследование строения пчелиных сотов и построение модели пчелиной ячейки.
- Практическое нахождение площади поверхности различных моделей пчелиной ячейки.
- Аналитическое нахождение площади поверхности правильной шестиугольной призмы (без нижнего основания) и площади поверхности соответствующей пчелиной ячейки и их разности.
Гипотеза исследования: шестигранная пчелиная ячейка – идеальная геометрическая форма для максимального использования единиц площади и объема: вмещает максимальное количество меда, и в то же время, для ее создания требуется минимальное количество воска.
Методы исследования: математический анализ, математическое моделирование, сравнительный анализ.
Задача изучения строения пчелиной ячейки является прикладной, решение которой, позволяет реализовать практическую (прикладную) направленность математики, что очень актуально в современное время.
Паркет из правильных многоугольников
Если разрезать пчелиные соты плоскостью, перпендикулярной их ребрам, то станет видна сеть равных друг другу правильных шестиугольников, уложенных в виде паркета. Возникает вопрос: «Почему пчелы строят соты именно так, почему они предпочли сеть правильных шестиугольников, а не правильных треугольников или квадратов, ведь их, казалось бы, гораздо проще сконструировать?»
Выясним, какими правильными многоугольниками можно заполнить плоскость так, чтобы не было пропусков. Уже пифагорейцам было известно, что имеется только три вида правильных многоугольников, которыми можно полностью замостить плоскость без пробелов и перекрытий: треугольник, квадрат и шестиугольник. В каждом из этих замощений любые два многоугольника имеют либо общую сторону, либо только общую вершину, либо вовсе не имеют общих точек. Замощения плоскости многоугольниками, удовлетворяющие этому требованию, называются паркетами. Убедиться в том, что никакой другой правильной многоугольник паркета не образует, можно с помощью формулы суммы внутренних углов выпуклого n-угольника: Сумма внутренних углов выпуклого n-угольника равна (n-2)*180о, где n- число сторон многоугольника. Сумма углов правильных n-угольников, сходящихся в одной вершине паркета, равна 360о. Тогда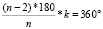 
, где k – число углов, сходящихся в одной вершине. Преобразуем это равенство: разделив левую и правую части на 1800*k, получим 
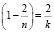или 
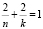. Отсюда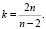 
Если n = 3, то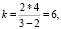 
т.е. в одной вершине паркета могут сходиться 6 правильных треугольников;
Если n = 4, то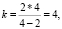 
т.е. в одной вершине паркета могут сходиться 4 квадрата;
Если n = 5, то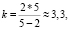 
т.е. не существует паркета из правильных пятиугольников;
Если n = 6, то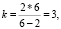 
т.е. в одной вершине паркета могут сходиться 3 правильных шестиугольника;
Если n = 7, то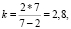 
т.е. не существует паркета из правильных семиугольников и т. д.
Так как внутренний угол правильного многоугольника меньше 1800, то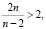 
значит, 
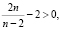или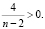 
По смыслу задачи значение n, k и -4/(n-2) могут быть только целыми, поэтому 4 делиться нацело на n-2. только когда n = 3, 4, 6.
Итак, мы выяснили, что заполнить плоскость без пропусков можно, используя или правильные треугольники, квадраты, или правильные шестиугольники. В паркете, составленном из правильных треугольников, в каждой точке сходятся шесть треугольников, из квадратов – четыре квадрата, из шестиугольников – три шестиугольника. Поэтому можно сделать вывод, что «мудрые пчелы» экономят воск и время для построения сотов в форме правильных треугольников.
Периметр равновеликих фигур
Развивая «пчелиную» тему выясним, какая из трех равновеликих друг другу фигур (фигуры называются равновеликими, если они имеют равные площади) – правильный треугольник, квадрат или правильный шестиугольник имеет меньший периметр?»
Пусть S – площадь каждой исследуемой фигуры, а3 – сторона правильного треугольника, а4 – сторона квадрата, а6 – сторона правильного шестиугольника, длины которых нужно вычислить для нахождения периметров соответствующих фигур.
1. Периметр правильного треугольника. Периметр P3 правильного треугольника вычислим по формуле P3 = 3a3. Для нахождения длины стороны a3 воспользуемся формулой нахождения площади треугольника: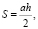 
где h – высота треугольника, проведенная к основанию а. Высоту найдем по теореме Пифагора:
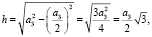
тогда
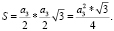
Итак, площадь правильного треугольника со стороной а3 вычисляется по формуле:
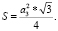
Зная площадь треугольника нетрудно вычислить длину стороны:
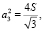
значит
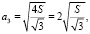
и так, как P3 = 3a3 то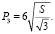 
2. Периметр квадрата. Аналогично вычислим периметр P4 квадрата со стороной a4:
Так, как S = a24 – площадь квадрата, то a4 = vS. P4 = 4a4, значит P4 = 4vS.
3. Периметр правильного шестиугольника. Вычислим площадь правильного шестиугольника. Шестиугольник состоит из шести правильных треугольников. Значит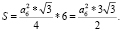 
Итак,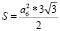 
– площадь правильного шестиугольника, тогда 
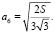Так, как P6 = 6a6, то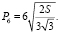 
Для сравнения периметров фигур найдем их отношение:
P3:P4:P6 = 6*v(S/v3)/4*vS/6*v(2S/(3v3)).
Разделив каждую часть отношения на vS, получим:
P3:P4:P6 =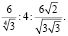 
Разделим еще каждую часть отношения на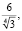 
получим:
P3:P4:P6 =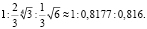 
Анализ результата вычислений позволяет сделать вывод: из трех правильных многоугольников с одинаковой площадью наименьший периметр имеет правильный шестиугольник. Стало быть, мудрые пчелы, и здесь экономят воск и время для построения сот.
Строение «пчелиной ячейки»
Исследуем дальше строение «пчелиной ячейки». Соты в улье свешиваются сверху вниз наподобие занавесок: пчелы прикрепляют их к потолку смесью воска и пчелиного клея (прополиса). «Пчелиные ячейки» представляют собой геометрически правильные шестигранные многогранники. Ячейки уложены в пласты и соприкасаются общими донышками. Но донышки ячеек не плоские, а представляют части трехгранных углов, гранями которых являются ромбы. Горизонтальный диаметр пчелиной ячейки – 5,3-5,7 мм (на 1 кв. см приходится около четырех ячеек), ее глубина – 10-12 мм.
1. Геометрическая интерпретация «пчелиной ячейки». Рассмотрим, как получается ячейка чисто геометрически.
В основе построения, очевидно, лежит построение изображение правильной шестиугольной призмы ABCDEFA1B1C1E1F1. Проведем диагонали верхнего основания призмы F1B1, B1D1, F1D1 и на оси призмы ОО1 возьмем некоторую точку S. Через прямые B1D1, F1D1 и точку S проведем три плоскости. Построим сечение призмы плоскостью (B1S1F1).Для этого достаточно построить точку пересечения ребра AA1 данной плоскостью: Точка Т является точкой пересечения диагоналей ромба F1A1B1O1 значит F1T = TB1. В свою очередь треугольник F1SB1 равнобедренный, ST является медианой, биссектрисой и высотой. ST лежит в плоскости сечения и пересекается с АА1 в искомой точке М. Аналогично строим точки L и K – точки пересечения плоскостей SB1D1 и F1D1S с ребрами CC1 и EE1 соответственно. Данные плоскости отсекают от призмы три равные треугольные пирамиды MB1F1A1, B1LD1C1, D1KF1E1.
Получившийся многогранник SABCDEFF1MB1LD1K и является моделью пчелиной ячейки. Построим развертку многогранника SABCDEF1MB1LD1K (одна ячейка сот).
3.2. Развертка. Для построения развертки модели пчелиной ячейки увеличим пропорционально размер натуральной ячейки. Сторона правильного шестиугольника – 3 см, глубина ячейки – 6,4 см. Поскольку боковая поверхность многогранника представляет собой шесть равных между собой трапеций, то для получения развертки построим эти трапеции. Построим отрезок АА = АВ + ВС + CD + DE + EF + FA. На продолжении ребра CL отложим отрезок LS, равный диагонали ромба. Из точки L проведем окружность радиусом, равным отрезку B1L. После этого построим середину отрезка LS, проведем через нее перпендикуляр к нему прямую, которая пересекает дугу окружности в двух вершинах ромба – B1 и D1. Два других ромба строим следующим образом: из вершины ромба D1 проводим окружность радиусом, равным стороне построенного ромба, а из вершины S – окружность, радиусом которой равен диагонали ромба. Эти окружности в пересечении дают еще одну вершину ромба – K. Для построения четвертой вершины ромба проведем из точки К окружность радиусом, равным стороне ромба, те же построения выполним из точки S. Точка пересечения этих окружностей и есть вершина ромба F1 . Аналогично строим вершины третьего ромба – F1, M, B1.
Построив развертку пчелиной ячейки нетрудно сконструировать модель пчелиной ячейки. На рис. 6 показано, как соприкасаются ячейки в улье. Их общая часть является ромбом.
Когда говорят о пчелиных сотах, то чаще всего демонстрируют рисунок, показывающий соты в разрезе плоскостью, перпендикулярной боковому ребру и пересекающей все соты по правильным шестиугольникам. Почему же все-таки пчелы строят донышки своих ячеек в форме части трехгранного угла, в качестве граней которого служат ромбы. Нельзя ли было поступить просто, сделать дно сот плоским, т.е. обычным правильным шестиугольником? Какая же здесь выгода для пчел? С чем это связано? С объемом или площадью боковой поверхности ячейки?
Для ответа на поставленные вопросы вычислим объем и площадь боковой поверхности многогранника SАВСВЕF1МВ1LD1К – модели пчелиной ячейки.
Объем «пчелиной ячейки»
Объем многогранника SАВСВЕF1МВ1LD1К равен объему правильной шестиугольной призмы АВСDEFA1B1C1D1E1F1: объем пирамиды B1D1F1S1 равен утроенному объему одной из равных пирамид F1B1O1S, B1D1O1S, SD1F1O1. Пирамиды МА1F1B1 и SO1B1F1 равны (они симметричны относительно точки Т). Это можно доказать: треугольники MA1T и SO1T равны по второму признаку равенства треугольников (если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны). Т – точка пересечения диагоналей ромба. АТ1 = ТО1, так как диагонали ромба точкой пересечения делятся пополам. Углы А1 и О1 – прямые и углы A1TM и SO1T равны, как вертикальные. Из равенства треугольников MA1T и SO1T следует равенство сторон MA1 и О1S. A1F1 и F1О1 равны, как стороны ромба. Треугольники SF1O1 и F1A1M равны по первому признаку равенства треугольников (если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны). ЗначитF1M = F1S. Аналогично можно доказать, что MB1 = B1F1, а B1F1 общая. Итак, пирамиды МА1F1B1 и SO1B1F1 равны. Что объем пирамиды D1D1F1S равен утроенному объему одной из равных пирамид можно наблюдать на подвижной модели пчелиной ячейки, которую мы сконструировали на основе модели правильной шестиугольной призмы.
Анализ проведенного исследования позволяет сделать вывод, что, объемы модели пчелиной ячейки и модели соответствующей правильной шестиугольной призмы равны.
Площадь поверхности «пчелиной ячейки»
Актуально исследовать равновеликие многогранники (правильная шестиугольная призма и «пчелиная ячейка») на равенство (или неравенство) площадей поверхностей.
Изготовив модели правильной шестиугольной призмы и «пчелиных ячеек» с разными положениями точки S, нетрудно вычислить экспериментально площадь боковой поверхности (без основания).
1. Площадь боковой поверхности правильной шестиугольной призмы. Площадь боковой поверхности правильной шестиугольной призмы (без нижнего основания) равна площади правильного шестиугольника, плюс шесть площадей прямоугольников. Сторона правильного шестиугольника равна 3 см, а высота (ребро) призмы равна 5,3 см.
Так как площадь правильного шестиугольника равна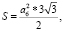 
то
Sпризмы
(см2) (без нижнего основания).
2. Площадь боковой поверхности модели «пчелиной ячейки». Площадь боковой поверхности модели «пчелиной ячейки» равна сумме площадей шести равных прямоугольных трапеций и трех ромбов:
Sпчелиной ячейки = 6*Sтрапеции+3*Sромба,
Sтрапеции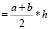 
(a, b – основания трапеции, h – высота),
Sромба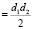 
, где d1, d2 – диагонали ромба.
Нами изготовлено пять моделей «пчелиных ячеек» с различными положениями точки S. Найдем площадь боковой поверхности каждой из них:
2.1. a = 5.3 см; b = 4.8 cм; h = 3 см, d1 = 5.2 см; d2 = 3.2 см.
Sтрапеции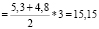 
(см2)
Sромба 
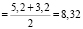(см2)
Sпчелиной ячейки = 6*15,15 + 3*8,32 = = 90,9 + 24,96 = 115,86 (см2).
2.2. a = 5.3 см; b = 4.6 см; h = 3 см; d1 = 5.2 см; d2 = 3.3 см.
Sтрапеции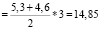 
(см2)
Sромба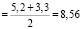 
(см2),
Sпчелиной ячейки = 25, 68 + 89, 10 = 114,78 (см2)
2.3. a = 5.3 см; b = 4.3 см; d1 = 5.2 см; d2 = 3.6 см; h = 3 см.
Sтрапеции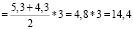 
(см2)
Sромба 
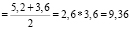(см2)
Sпчелиной ячейки = 86,4+28,08 = 114,48 (см2)
2.4. a = 5,3 см; b = 3,8 см; d1 = 5.2 см; d2 = 4,2 см; h = 3 см
Sтрапеции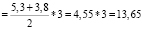 
(см2)
Sромба 
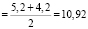(см2)
Sпчелиной ячейки = 6*13, 65 + 3*10,92 = = 81,9 + 32,76 = 114,66 (см2).
a = 5,3 см; b = 3,5 см; d1 = 5.2 см; d2 = 4,7 см; h = 3 см.
Sтрапеции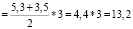 
(см2)
Sромба 
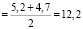(см2)
Sпчелиной ячейки = 6*13,2+3*12,22 = = 79,2 + 36,66 = 115,86 (см2)
Анализ результатов вычислений позволяет сделать вывод: площадь боковой поверхности пчелиной ячейки меньше, чем площадь боковой поверхности соответствующего правильного шестиугольника.
При увеличении расстояния O1S площадь боковой поверхности пчелиной ячейки уменьшается до определенного значения, а потом начинает возрастать. Возникает вопрос:
При каком же положении точка S на оси ОО1 площадь поверхности многогранника наименьшая?
3. Наименьшая площадь поверхности «пчелиной ячейки».
Пусть АВ = а, ВВ1 = b, SO1 = x, причем 0 < x < ∞.
Определим значение переменной х, при котором площадь поверхности многогранника-ячейки наименьшая. Пусть Q(x) – площадь поверхности многогранника ячейки (без нижнего основания), и для ее нахождения достаточно найти площадь ромба и площадь трапеции.
3.1. Площадь ромба. Sромба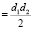 
, найдем d1 и d2.
ТреугольникB1A1F1 – равнобедренный, угол при вершине равен 1200 А1Т – медиана, биссектриса, высота. Треугольник A1TB1 – прямоугольный, угол В1А1Т = 600, угол АВ1Т = 300. Т.к. в прямоугольном треугольнике против угла 300 лежит катет равный половине гипотенузы, то А1Т = а/2.
Находим B1T =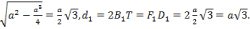 
d1 = av3
Рассмотрим треугольник SO1T: SO1 = x
O1T = A1T =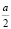 
, ST = 
;
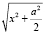тогда
d2 = MS = 2ST =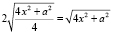 
Sромба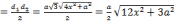
3.2. Площадь трапеции
Sтрапеции =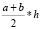 
.
Рассмотрим трапецию ABB1M, где AB = a; BB1 = b; AM = b-x, тогда
Sтрапеции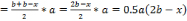 
Значит Q(x) =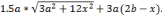 
3.3. Наименьшая площадь поверхности «пчелиной ячейки». Для ответа на вопрос задачи о наименьшей площади поверхности надо найти минимум функции Q(x), заданной на множестве положительных чисел.
Найдем критическую точку Q(x):
Q,(x) =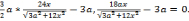 
Поскольку 3a2 + 12x2 > 0 и по условию х > 0 имеем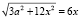 
, отсюда 
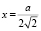, легко проверить, что при 0 < x < 2v2 производная S,(x), больше 0. Функция Q(x) непрерывна на всей области определения, других минимумов на интервале (0; ∞) не имеет, поэтому в точках 
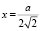она принимает свое наименьшее значение 
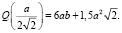Площадь поверхности правильной шестиугольной призмы без нижнего основания равна 
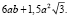Площадь поверхности ячейки равна 
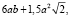ее объем равен объему той же шестиугольной призмы.
Таким образом, площадь поверхности Q1 правильной шестиугольной призмы АВСDEFA1B1C1D1E1F1 равна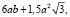 
а площадь поверхности Q2 соответствующей пчелиной ячейки 
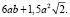Найдем, сколько же сэкономят пчелы на постройке всего лишь одной ячейке сот. Для этого найдем разность площадей Q1 – Q2 = 
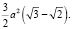Как видим, пчелиная ячейка имеет объем, как и правильная шестиугольная призма, а так как площадь ее поверхности меньше площади поверхности призмы, то остается удивляться экономичности пчел.
Какова же разность площадей поверхности правильной шестиугольной призмы (без нижнего основания) и соответствующей пчелиной ячейки?
Q1-Q2 =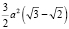 
; а ≈ 5,6 мм,
тогда
Q1-Q2 =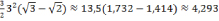 
(см2),
то есть Q1 > Q2 на 0,15 см2.
При постройке 100 ячеек экономиться около 15 см2 площади поверхности. А сколько же экономиться воска? В имеющейся литературе приводятся сведенья о том, что благодаря такой «математической» работе расчетливые «геометры» экономят около 2 % воска. Количество воска, сэкономленного при постройке 54 ячеек, может быть использовано для одной такой же.
Заключение
Проведя анализ результатов проделанной работы, сделаны следующие выводы:
1. При замощении плоскости правильными многоугольниками можно, использовать только правильные треугольники, квадраты или правильные шестиугольники. В паркете, составленном из правильных треугольников, в каждой точке сходятся шесть треугольников, из квадратов – четыре квадрата, из шестиугольников – три шестиугольника. Кроме того, при условии одинаковой площади данных многоугольников наименьший периметр имеет правильный шестиугольник. Таким образом, только используя данную фигуру в построении сотов, пчелы максимально сокращают расход воска и времени.
2. Пчёлы строят донышки своих ячеек в форме части трёхгранного угла, в качестве граней которого служат ромбы. Общая часть соприкосновения ячеек в улье является ромбом.
3. Объёмы многогранника «пчелиной ячейки» и правильной шестиугольной призмы равны, в то время, как площадь поверхности, многогранника «пчелиной ячейки» меньше, что выгодно с экономической точки зрения.
4. Пчелиные соты представляют собой пространственный паркет, поскольку они заполняют пространство так, что не остаётся просветов.
Полученные выводы подтверждают выдвинутую гипотезу: шестигранная «пчелиная ячейка» – идеальная геометрическая форма для максимального использования единиц площади и объема: вмещает максимальное количество меда, и в то же время, для ее создания требуется минимальное количество воска. То есть пчела использует наиболее выгодную из всевозможных форм.
Принцип построения пчелиных сотов широко используется в архитектурных ансамблях всего мира, в строительстве гигантских сооружений, Мобильные, или сотовые, телефоны работают, благодаря созданию особой сотовой сети. Сеть создана по принципу устройства пчелиных сот.
Так с помощью геометрии, математического анализа и математического моделирования мы прикоснулись к тайне математических шедевров из воска, еще раз убедившись во всесторонней развитости математики.
Библиографическая ссылка
Чепурко Н.А. МАТЕМАТИЧЕСКИЕ ТАЙНЫ ПЧЕЛИНОЙ ЯЧЕЙКИ // Международный школьный научный вестник. – 2018. – № 3-2. ;URL: https://school-herald.ru/ru/article/view?id=545 (дата обращения: 30.12.2024).