Данная статья является реферативным изложением основной работы. Полный текст научной работы, приложения, иллюстрации и иные дополнительные материалы доступны на сайте V Международного конкурса научно-исследовательских и творческих работ учащихся «Старт в науке» по ссылке: https://school-science.ru/5/11/33832
Турбулентные процессы наверняка ощущал каждый, кто хотя бы пару раз летал на самолете. Иногда она почти не заметна, а иногда становится причиной травм пассажиров и серьезных повреждений техники. Как сообщает Федеральное Агентство по гражданской авиации США (FAA), за год более 1000 человек получают травмы во время перелетов из-за турбулентности. Турбулентность неблагоприятно действует на навигационные приборы, вызывая помехи, а порой и повреждения. Ученые придумывают все новые способы, как ослабить это явление. Но существуют случаи, когда турбулентность играет на руку человеку. Один из примеров таких случаев меня и заинтересовал. Это смешивание топлива в двигателях в турбулентных потоках. В этом случае турбулентность помогает в убыстрении процесса смешивания, а как следствие и горения.
Увеличение скорости получения горючей смеси и ее горения одна из важнейших задач современного инженера. Поэтому использование турбулентности весьма актуально. Подробнее о турбулентности и ее применении в строении двигателей я расскажу в своем проекте.
1. Что такое турбулентность?
При определенных параметрах турбулентность наблюдается в потоках жидкостей и газов, многофазных течениях, жидких кристаллах, квантовых бозе- и ферми- жидкостях, магнитных жидкостях, плазме и любых сплошных средах (например, в песке, земле, металлах). Турбулентность также наблюдается при взрывах звезд, в сверхтекучем гелии, в нейтронных звездах, в легких человека, движении крови в сердце, при турбулентном (т. н. вибрационном) горении.
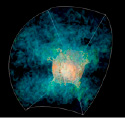
Турбулентность возникает самопроизвольно, когда соседние области среды следуют рядом или проникают один в другой, при наличии перепада давления или при наличии силы тяжести, или когда области среды обтекают непроницаемые поверхности. Она может возникать при наличии вынуждающей случайной силы. Обычно внешняя случайная сила и сила тяжести действуют одновременно. Например, при землетрясении или порыве ветра падает лавина с горы, внутри которой течение снега турбулентно.
Мгновенные параметры потока (скорость, температура, давление, концентрация примесей) при этом хаотично колеблются в округ средних значений. Зависимость квадрата амплитуды от частоты колебаний (или спектр Фурье) является непрерывной функцией.
Турбулентность – явление, заключающееся в том, что, обычно, при увеличении скорости течения жидкости или газа в среде самопроизвольно образуются многочисленные нелинейные фрактальные волны и обычные, линейные различных размеров, без наличия внешних, случайных, возмущающих среду сил и/или при их присутствии. Для расчета подобных течений были созданы различные модели турбулентности. Волны появляются случайно, и их амплитуда меняется хаотически в некотором интервале. Они возникают чаще всего либо на границе, у стенки, и/или при разрушении или опрокидывании волны. Они могут образоваться на струях. Экспериментально турбулентность можно наблюдать на конце струи пара из электрочайника.
Турбулентность в ее обычном понимании возникает в пристеночных слоях слабовязких жидкостей или газов либо на некотором удаленном расстоянии за плохообтекаемыми телами. Скорее всего, турбулентность описывается уравнением Больцмана, поскольку характерные масштабы этого уравнения намного меньше масштабов турбулентности.
Уравнение Больцмана описывает эволюцию во времени (t) функции распределения плотности f(x, p, t) в одночастичном фазовом пространстве, где x и p – координата и импульс соответственно. Распределение определяется так, что
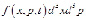
пропорционально числу частиц в фазовом объеме d³x d³p в момент времени t. Уравнение Больцмана
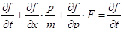
Здесь F(x, t) – поле сил, действующее на частицы в жидкости или газе, а m – масса частиц. Слагаемое в правой части уравнения добавлено для учета столкновений между частицами.
Но вопрос остается открытым, в настоящее время ведутся исследования о применимости этого уравнения для моделирования процесса возникновения турбулентности. Чаще всего в качестве математического описания турбулентности используют уравне́ния Навье́ – Сто́кса это – система дифференциальных уравнений в частных производных, описывающая движение вязкой ньютоновской жидкости. Уравнения Навье – Стокса являются одними из важнейших в гидродинамике и применяются в математическом моделировании многих природных явлений и технических задач. Названы по имени французского физика Анри Навье и британского математика Джорджа Стокса.
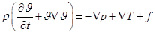
Однако до настоящего момента не получено ни одного точного аналитического решения этой системы уравнений для турбулентной области течения. Проблема заключается в том, что уравнения движения жидкости (уравнения Навье-Стокса) являются безмасштабными, то есть сами по себе не задают пределов прямого каскада и таким образом не определяют характерного размера (масштаба) турбулентных вихрей. Тем не менее, на их основе разработано огромное множество математических моделей турбулентности (RANS, LES, DES и DNS модели). Эти модели, за исключением модели DNS, широко используются для инженерных расчетов. В случае несжимаемой жидкости система состоит из двух уравнений:
• уравнения движения,
• уравнения неразрывности.
В гидродинамике обычно уравнением Навье – Стокса называют только одно векторное уравнение движения. Впервые уравнение Навье – Стокса было получено Навье (1822, несжимаемая жидкость) и Пуассоном (1829, сжимаемая жидкость), которые исходили из модельных представлений о молекулярных силах. Позже феноменологический вывод уравнения был дан Сен-Венаном и Стоксом. Обычно турбулентность наступает при превышении критической величины неким параметром, например числом Рейнольдса или Релея (в частном случае скорости потока при постоянной плотности и диаметре трубы и/или температуры на внешней границе среды). Количественные условия перехода к турбулентности были экспериментально открыты английским физиком и инженером О. Рейнольдсом в 1883 году при изучении течения воды в трубах. Число Рейнольдса – величина, характеризующая отношение нелинейного и диссипативного членов в уравнении Навье – Стокса. Число Рейнольдса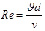 
также считается критерием подобия течения вязкой жидкости.
2. Смешивание и горение
в турбулентном потоке
Турбулентность, например, можно создать, если:
• увеличить линейную скорость или угловую скорость вращения потока, размер обтекаемого тела, уменьшить первый или второй коэффициент молекулярной вязкости, увеличить плотность среды;
• нагреть среду;
• уменьшить вязкость;
• увеличив угловую скорость вращения или радиальный градиент
температуры;
• задав очень сложный вид внешней силы (примеры: хаотичная сила, удар). Течение может не иметь фрактальных свойств.
• создав сложные граничные или начальные условия, задав функцию формы границ. Например, их можно представить случайной функцией. Например: течение при взрыве сосуда с газом. Или организовать вдув газа в среду, создать шероховатую поверхность. Использовать разгар сопла. Поставить сетку в течение. Течение может при этом не иметь фрактальных свойств.
• облучив среду звуком высокой интенсивности.
• с помощью химических реакций, например горения. Форма пламени, как и вид водопада может быть хаотичной.
Рассмотрим более подробно последний аспект возникновения турбулентности в процессе сгорания топлива в тепловых двигателях, который непосредственно связан с запуском летательных аппаратов. Тепловой двигатель – устройство, преобразующее внутреннюю энергию топлива в механическую энергию. К тепловым двигателям относятся: паровая машина, двигатель внутреннего сгорания, паровая и газовая турбины, реактивный двигатель. Их топливом является твердое и жидкое топливо, солнечная и атомная энергии.
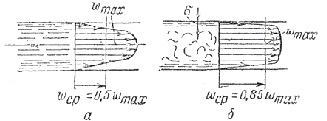
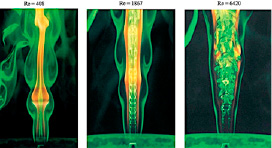
Горение топлива в тепловых двигателях обычно происходит в сильно турбулизованном потоке. Турбулентный поток характеризуется неупорядоченным движением частиц газа, при котором скорость в каждой точке потока меняется по направлению и по величине. Для турбулентного потока характерно наличие пульсаций скорости, давления, температуры и концентрации вещества.
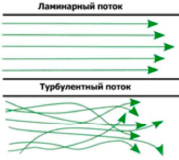
Молекулярный механизм передачи тепла и массы вещества интенсифицируется пульсациями и перемешиваниями отдельных объемов газовой смеси. В мелкомасштабных молях происходит быстрый процесс молекулярного перемешивания, в частности происходит перемешивание продуктов сгорания со свежей смесью. В тех молях, где получающаяся после смешения температура достаточно высока, смесь успевает сгореть по законам объемной реакции раньше, чем в таком медленном процессе, как ламинарное горение. Образующиеся при этом продукты реакции опять смешиваются с молями свежей смеси и, таким образом, происходит распространение пламени. В тех молях, где температура после смешения слишком мала, реакция горения за время существования моля не успевает завершиться. Кроме того, в зоне горения должны также существовать моли, состоящие только из свежей смеси или только из продуктов реакции и в данный момент не участвующие в горении. Можно предполагать, что суммарная скорость горения в этом случае будет значительно превышать скорость ламинарного горения, так как молекулярно-турбулентное смешение происходит с большей скоростью, чем ламинарное. Ламинарное течение – течение, при котором жидкость или газ перемещается слоями без перемешивания и пульсаций (то есть без беспорядочных быстрых изменений скорости и давления).
Скорость распространения пламени зависит также от состояния смеси перед воспламенением. Если смесь неподвижна или течет ламинарно, то процессы переноса во фронте пламени осуществляются за счет молекулярной диффузии и теплопроводности. Такое распространение пламени называют ламинарным. Если горючая смесь находится в турбулентном движении, то молекулярная диффузия начинает играть второстепенную роль – ведущее значение в распространении пламени приобретают процессы турбулентного смешения свежей смеси с продуктами сгорания. Подобное горение называют турбулентным.
Смесители для жидкостей работают преимущественно по механизму ламинарного смешения, сопровождающегося увеличением площади поверхности раздела между компонентами и распределением элементов поверхности раздела внутри объема смесителя. Конструкция такого смесителя зависит от вязкости смесей. Например, для низковязких жидкостей применяют лопастные и высокоскоростные диспергирующие смесители. При малой вязкости смеси существенную роль может играть турбулентное смешение. Для смесей со средними значениями вязкости используют разнообразные двухроторные смесители, например смеситель с 2-образными роторами. Такой смеситель представляет собой камеру, образованную двумя полуцилиндрами. В камере установлены два ротора, вращающиеся навстречу друг другу с различной скоростью. Обычно отношение скоростей вращения роторов составляет 2/1. Смешение происходит вследствие взаимного наложения тангенциального и осевого движений материала. Чтобы исключить возможность образования застойных зон, зазор между роторами и стенкой камеры делают небольшим – около 1 мм. Такие смесители используют для смешения жидкостей с вязкостью 0,5—500 Па-с. К двухроторным относятся также смесители с зацепляющимися роторами, вращающимися с одинаковой скоростью. Двухроторные смесители широко используют для изготовления наполненных пластмасс, а также для смешения различающихся по вязкости жидкостей и паст.
3. Различные подходы в описании турбулентности
Для теоретического описания турбулентности применяются различные подходы. При статистическом подходе считается, что турбулентность порождает случайно изменяющаяся совокупность вихревых элементов различных размеров. Другим подходом является метод спектрального анализа, который дополняет статистический подход.
При больших числах Рейнольдса, скорости потока от небольших изменений на границе зависят слабо. Поэтому при разных начальных скоростях движения корабля формируется одна и та же волна перед его носом, когда он движется с крейсерской скоростью. Нос ракеты обгорает и создается одинаковая картина разгара, несмотря на разную начальную скорость.
Фрактальный – означает самоподобный. У прямой линии фрактальная размерность равна единице. У плоскости равна двум. У шара трем. Русло реки имеет фрактальную размерность больше 1, но меньше двух, если рассматривать его с высоты спутника. У растений фрактальная размерность вырастает с нуля до величины больше двух. Есть характеристика геометрических фигур, называется фрактальная размерность. Наш мир нельзя представить в виде множества линий, треугольников, квадратов, сфер и других простейших фигур. И фрактальная размерность позволяет быстро характеризовать геометрические тела сложной формы. Например, форму листа дерева. Нелинейная волна – волна, которая обладает нелинейными свойствами. Их амплитуды нельзя складывать при столкновении. Их свойства сильно меняются при малых изменениях параметров. Нелинейные волны называют диссипативными структурами. В них нет линейных процессов дифракции, интерференции, поляризации. Но есть нелинейные процессы, например, самофокусировка. При этом резко, на порядки увеличивается коэффициент диффузии среды, перенос энергии и импульса, сила трения на поверхность. То есть, в частном случае, в трубе с абсолютно гладкими стенками при скорости выше некоторой критической, в течение любой сплошной среды, температура которой постоянная, под действием только силы тяжести всегда самопроизвольно образуются нелинейные самоподобные волны и затем турбулентность. При этом нет никаких внешних возмущающих сил. Если дополнительно создать возмущающую случайную силу или ямки на внутренней поверхности трубы, то турбулентность также появится. В частном случае нелинейные волны – вихри, торнадо, солитоны и другие нелинейные явления (например, волны в плазме – обычные и шаровые молнии), происходящие одновременно с линейными процессами (например, акустическими волнами). На математическом языке турбулентность означает, что точное аналитическое решение дифференциальных уравнений в частных производных сохранений импульса и сохранения массы Навье-Стокса (это закон Ньютона с добавлением сил вязкости и сил давления в среде и уравнение неразрывности или сохранения массы) и уравнение энергии представляет собой при превышении некоторого критического числа Рейнольдса, странный аттрактор. Они представляют нелинейные волны и обладают фрактальными, самоподобными свойствами. Но так как волны занимают конечный объем, какая-то часть области течения ламинарна. При очень малом числе Рейнольса – это всем известные линейные волны на воде небольшой амплитуды. При большой скорости мы наблюдаем нелинейные волны цунами или обрушение волн прибоя. Например, крупные волны за плотиной распадаются на волны меньших размеров. Вследствие нелинейных волн любые параметры среды: (скорость, температура, давление, плотность) могут испытывать хаотические колебания, изменяются от точки к точке и во времени непериодически. Они очень чувствительны к малейшим изменением параметров среды. В турбулентном течении мгновенные параметры среды распределены по случайному закону. Этим турбулентные течения отличаются от ламинарных течений. Но управляя средними параметрами, мы можем управлять турбулентностью. Например, изменяя диаметр трубы, мы управляем числом Рейнольдса, расходом топлива и скоростью заполнения бака ракеты. Уравнения Навье – Стокса (обычные, а не усредненные по какому-то интервалу времени) описывают и мягкую, и жесткую потерю устойчивости течений. Их можно вывести тремя способами из общих законов сохранения: постулируя закон трения Ньютона(обобщенный), следуя методу Чепмена-Энскога и из метода Грэда. При вязкости равной нулю уравнения сводятся к уравнению Эйлера. Точные решения уравнения Эйлера также хаотичны. Общепринято считать проекцию вектора скорости на ось координат в турбулентном потоке, состоящей из средней или осредненной величины, за некоторое выбранное время, и плюс мгновенной составляющей. Турбулентное течение с большим числом Рейнольдса называют развитой турбулентностью. При разных граничных условиях оно всегда приводит к созданию одного и того же профиля скоростей. Это свойство независимости параметров от числа Рейнольдса называют автомодельностью течения. Наблюдается экспериментально в струях или в пограничном слое. Можно создать изотропную турбулентность, когда статистические параметры течения (функция распределения вероятности, дисперсия, моменты) одинаковы в направлении разных осей координат и не зависят от времени. Теория однородной турбулентности (то есть, при очень больших числах Рейнольдса, когда ее статистические параметры не зависят от времени и примерно постоянны в течении, но зависят от направления) была создана советскими учеными Обуховым и Колмогоровым. И использовалась затем во многих инженерных расчетах. Теория привела к созданию упрощенных полуэмпирических моделей течения: k-ε (ка-эпсилон) и многих других. Большинство течений жидкостей и газов в природе (движение воздуха в земной атмосфере, воды в реках и морях, газа в атмосферах Солнца и звезд и в межзвездных туманностях и т. п.), в технических устройствах (в трубах, каналах, струях, в пограничных слоях около движущихся в жидкости или газе твердых тел, в следах за такими телами и т. п.) турбулентны из-за наличия источников энергии и импульса, наличия внешних возмущающих сил или отсутствия сил сопротивления трения в квантовых жидкостях. При процессах горения или химических реакциях на явление турбулентности накладываются множество других физических и химических процессов. Например, эффект конвекции, автоколебаний, гистерезиса. В этом случае говорят о турбулентной конвекции. Обычно принимается, что переход от ламинарного течения к турбулентному происходит при достижении критического числа Рейнольдса (Re). Критическое значение числа Рейнольдса зависит от конкретного вида течения, его коэффициента вязкости, который зависит от температуры, которое зависит от давления (течение в круглой трубе, обтекание шара и т. п.). В последнее время показано, что это правомерно только для напорных потоков. Но удар по трубе, ее резкое вращение или колебание могут вызвать появление турбулентности. То есть, турбулентность может возникать самопроизвольно, а может в результате действий нескольких внешних сил. При изучении течения жидкости через трубки малого диаметра французским врачом и ученым Пуазейлем в 1840—1842 гг. выведена формула, по которой можно рассчитать расход воды через трубу. До Пуазейля исследованием движения вязкой жидкости через трубы малого диаметра занимался Хаген (1797—1884). При большом расходе формула оказалась неверной. Причина в том, что в трубе возникала турбулентность. Стоксом были найдены решения уравнения движения вязкой жидкости для малых чисел Re (это второй закон Ньютона с добавками сил давления и сил вязкости), которые он вывел в 1845 г. для движения жидкости в круглой трубе. Затем он получил формулу силы сопротивления при равномерном движении шара в неограниченной жидкости в 1851 году. Ее стали использовать для определения коэффициента динамической вязкости. Но решения совпали с опытом лишь при малых скоростях движения жидкости и диаметрах трубы и шара. Причина этого расхождения была объяснена только опытами Рейнольдса в 1883 г. Он показал существование двух различных режимов движения жидкости – ламинарного и турбулентного – и нашел один параметр – число Рейнольдса – который позволил предсказать наличие турбулентности для данного течения в трубе. Если бы Стокс нашел точные решения Навье-Стокса, он бы обнаружил турбулентность теоретически. Это позволило Рейнольдсу в 1883 г. ввести положение, что течения одинакового типа (труба должна быть геометрически подобной) с одинаковым числом Рейнольдса подобны. Этот закон был назван законом подобия. Затем, на основе опытов, стала развиваться теория размерности и подобия. Так как Хаген не знал, как выглядят уравнения Навье-Стокса, что такое число подобия Рейнольдса, то нельзя говорить, что он или Леонардо да Винчи открыл турбулентность. Они наблюдали хаотическое движение в воде. Но описать количественно, предсказать его наступление не могли. А подобие течения, рождение самоподобных структур, например вихрей, которые сами состоят из таких же вихрей – основное свойство турбулентности. То есть Рейнольдс как бы открыл то, что уравнение для силы гравитации и закон Кулона подобны с разницей только в коэффициенте. А Хаген и Пуазейль только нашли отдельные параметры, которые входят в точное решение уравнения Навье-Стокса и влияют на течение. Частичное описание развитой турбулентности в рамках математики XIX века предложил Л. Ричардсон в начале XX века. Мешая ложкой чай в стакане, мы создаем вихри размером порядка размера стакана, ложки. Вязкость действует на течение тем сильнее, чем меньше характерный размер течения. Под характерным размером понимают какой-то геометрический параметр, сильно влияющий на течение. Диаметр стакана, его высота, ширина ложки. При большом числе Рейнольдса на эти крупномасштабные движения молекулярная вязкость действует слабо. Уравнение движения жидкости (Навье-Стокса) нелинейно, так как скорость жидкости переносится самой скоростью и эти вихри неустойчивы. Они дробятся на более мелкие вихри, те на более мелкие. В конце концов на малых размерах вступает в действие молекулярная вязкость, и самые мелкие вихри затухают за счет нее. Эта представление назвали прямой каскад (или переход от больших масштабов в меньшие). Турбулентность формально связана с биологическими объектами, с процессами митоза и роста некоторых раковых опухолей, с теорией радиоактивного распада, с процессами, происходящими на рынках акций. Есть разница между понятием турбулентность и турбулентное течение. Термин турбулентное течение возник в гидравлике. Затем были открыты квантовые жидкости. Их вязкость всегда равна нулю. Если подсчитать для них число Рейнольдса, оно всегда равно бесконечности, когда проекция вектора скорости не равна нулю. Само турбулентное течение может присутствовать в системе очень мелких вихрей, в некоторых малых частях среды. Поэтому, средняя скорость течения равна нулю, когда квантовая жидкость покоится в сосуде. Число Рейнольдса не определено (в числителе нулевая скорость, в знаменателе нулевая вязкость).
4. Фрактальное представление турбулентности
Прежде чем говорить о фрактальном представлении волн турбулентности, надо упомянуть, что же такое фрактал. Фрактал – это математическое множество, обладающее свойством самоподобия. Первые примеры самоподобных множеств с необычными свойствами появились в XIX веке в результате изучения непрерывных недифференциируемых функций (например, функция Больцано, функция Вейерштрасса, множество Кантора). Термин «фрактал» введен Бенуа Мандельбротом в 1975 году и получил широкую известность с выходом в 1977 году его книги «Фрактальная геометрия природы». Особую популярность фракталы обрели с развитием компьютерных технологий, позволивших эффектно визуализировать эти структуры.
Слово «фрактал» употребляется не только в качестве математического термина. Фракталом может называться предмет, обладающий, по крайней мере, одним из указанных ниже свойств:
• Обладает нетривиальной структурой на всех масштабах. В этом отличие от регулярных фигур (таких как окружность, эллипс, график гладкой функции): если мы рассмотрим небольшой фрагмент регулярной фигуры в очень крупном масштабе, то он будет похож на фрагмент прямой. Для фрактала увеличение масштаба не ведет к упрощению структуры, то есть на всех шкалах мы увидим одинаково сложную картину.
• Является самоподобным или приближенно самоподобным.
• Обладает дробной метрической размерностью или метрической размерностью, превосходящей топологическую.
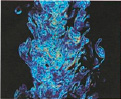
Многие объекты в природе обладают свойствами фрактала, например: побережья, облака, кроны деревьев, снежинки, кровеносная система, система альвеол человека или животных.
Увидеть турбулентность крайне сложно без специального оборудования, но можно прибегнуть к компьютерному моделированию и использовать фрактальную структуру турбулентности. Турбулентный вихрь сам состоит из подобных ему завихрений. Используя язык программирования Java, я попытался создать модель турбулентного фрактального вихря (см. полный текст работы. ПРИЛОЖЕНИЕ 1). За основу взял дугу полуокружности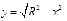 
, применив поворот, «раскопировал» ее 15 раз и получил модель одного вихря.
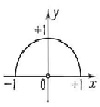
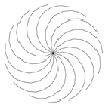
На середине каждой дуги был построен еще один «вихрь», а на серединах новых «вихрей» следующие. В итоге после одной итерации получаем 15 вихрей, в результате второй 225, после третьей 153 и т.д. В результате имеем следующий фрактал, который визуально напоминает «вихрь» или воронку, а сам он состоит из таких же самоподобных вихрей.
Заключение
Исследования турбулентных течений, этой все еще наиболее трудной проблемы гидродинамики, продолжают приносить важные технологические достижения, однако путь к прогрессу здесь никак не назовешь прямым. История исследований турбулентных течений научными методами насчитывает приблизительно сто лет, и на протяжении этого периода времени некоторые из наиболее великих умов в области физики, механики и техники пробовали иногда свои силы в решении имеющихся здесь проблем. Было достигнуто продвижение вперед по многим направлениям исследований, и в итоге мы видим действительно заметный прогресс в наших знаниях о предмете. Тем не менее «проблема турбулентности» в целом, что бы она ни означала, все еще сохраняется. С точки зрения теории новый интерес к идеям распространения вихрей в невязкой жидкости и кинематике вихревых взаимодействий оказывается неслучайным. Заслуживает внимания и вопрос о естественных или неустранимых вихревых образованиях. Наиболее важным аспектом существования в турбулентном потоке детерминированных структур является возможность воздействия на турбулентность путем прямой интерференции этих крупномасштабных структур. Такое воздействие могло бы привести к очень важным для техники достижениям. Турбулентность и теперь, и в будущем останется одной из наиболее трудных проблем гидродинамики, и имеющийся здесь опыт позволяет предположить, что последующее падение интереса к когерентным структурам более чем вероятно. Итоговый рост наших знаний о турбулентности может оказаться ниже уровня сегодняшних больших ожиданий, но в любом случае он будет положительным.
Библиографическая ссылка
Кузнецов Д.В. ТУРБУЛЕНТНОСТЬ. СМЕШИВАНИЕ ЖИДКОСТЕЙ В ТУРБУЛЕНТНОМ ПОТОКЕ // Международный школьный научный вестник. – 2018. – № 5-3. ;URL: https://school-herald.ru/ru/article/view?id=696 (дата обращения: 26.12.2024).