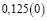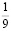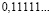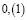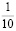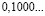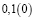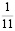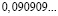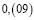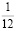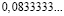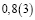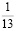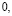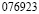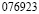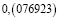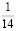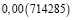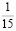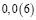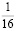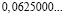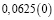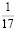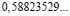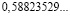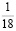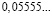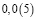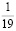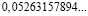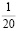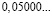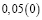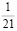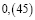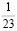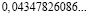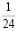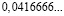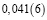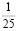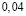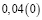Человек подобен дроби: числитель – это он сам,
а знаменатель то, что он сам о себе думает.
Чем больше знаменатель, тем меньше дробь.
Л.Н. Толстой
Целью исследования было изучение и экспериментальная проверка свойств аликвотных дробей.
Задачи:
• Изучить литературу по теме, включая исторические сведения.
• Ознакомиться с понятием «аликвотные дроби», изучить историю их возникновения.
• Изучить сами аликвотные и бесконечные периодические дроби.
• Выбрать группу аликвотных дробей для исследования, научиться раскладывать дроби на аликвотные.
• Сформулировать выявленные свойства.
• Научиться решать задачи с применением аликвотных дробей.
Объект исследования: аликвотные дроби с знаменателями меньше 100.
Предмет исследования: применение известных свойств действий над числами к аликвотным дробям.
Гипотеза: групп аликвотных дробей, обладающих одинаковыми свойствами, не существует.
Проблема исследования заключается в выявлении групп аликвотных дробей, обладающих одинаковыми свойствами.
Актуальность исследования: аликвотные дроби находят применение в различных областях науки и ее многочисленных приложениях, в особенности это относится к математике, физике и химии и даже музыке.
Я впервые услышал об аликвотных дробях по телевизору. Сначала меня заинтересовало само название. Мне стало интересно, когда впервые человечество узнало аликвотные дроби, как они использовались при решении практических задач, какими известными свойствами чисел обладают эти дроби. Меня заинтересовали задачи на применение аликвотных дробей, поэтому я занялся исследованием свойств аликвотных дробей, находя исторические и научные сведения по этому вопросу.
Методы исследования:
1. Изучение информационных источников: историческая и научная литература, энциклопедические словари, интернет-источники.
2. Анкетирование одноклассников, друзей и их родителей.
3. Обобщение экспериментального и теоретического материала, рефлексивное осмысливание результатов сформулированных свойств.
4. Решение задач с использованием аликвотных дробей и их свойств.
Хочу предположить, что тема моего исследования хоть и не столь актуальна, но точно будет интересна каждому человеку, начиная с самого раннего возраста.
Разве не пытался кто-то из вас разделить одно целое на несколько частей: ну хотя бы торт на дне рождения поровну по количеству присутствующих гостей? Даже школьник сталкивался с подобной задачей. А как это сделать грамотно и, тем более, с наименьшим количеством шагов?
Оказывается, это легко решается с использованием аликвотных дробей.
Вот простой пример:
Рассмотрим практическую задачу, известную из древне: «Необходимо разделить 7 хлебов между 8 людьми поровну».
Думаю, что каждый решал бы задачу так: надо разрезать каждый хлеб на 8 равных частей, раздав каждому человеку по одной части от каждого хлеба, т.е. семь восьмушек.
А вот как эта задача решена с помощью аликвотных дробей, описанная на папирусе Райнда – это древнеегипетский математический текст, переписанный около 1650 г. до н.э. писцом Ахмесом.
Поскольку 7/8 = 1/2 + 1/4 + 1/8. Следовательно, каждому человеку нужно дать по половине, четверти и восьмушке хлеба. Теперь ясно, что надо 4 хлеба разрезать пополам, 2 хлеба – на 4 части и только один хлеб – на 8 частей. И если нашему современнику надо было бы сделать 49 разрезов, то египтянину – всего 17, т.е. египетский способ почти в 3 раза экономичнее.
Вот так, собирая интересную информацию, вопросов не убавлялось, они расширялись и углублялись в интересующую меня тему. Я получал ответы на свои вопросы от родителей, своего учителя, а затем в различных энциклопедиях, Интернете, литературе…
И мне захотелось узнать, как при решении многих жизненных задач, требующих длинных и сложных вычислений, найти простое, рациональное, короткое и изящное решение. Упрощается ли решение задач, если использовать аликвотные дробй Это определило тему моего исследования.

Анкетирование
Узнав много интересного об аликвотных дробях, мне захотелось понять: а что знают о них ребята нашего класса, мои друзья и их родители. Поэтому мною было проведено анкетирование среди них. Я предложил им следующие 5 вопросов и задачу:
1. Знаете ли Вы, что такое «Аликвотные дроби»?
2. Знаете ли Вы, когда впервые начали использовать аликвотные дроби и где?
3. Знаете ли Вы, как назывались аликвотные дроби на Русй
Например, 1/3; 1/4; 1/6; 1/8…
4. Знаете ли Вы, что такое ГЛАЗ ГОРА?
5. Знаете ли Вы, что такое аликвотные струны?
6. Решите задачу: Разделите 7 хлебов между 8 людьми поровну.
Сколько разрезов будет сделано?
|
№ |
Вопрос |
Уч.1 |
Уч.2 |
Уч.3 |
Уч.4 |
Уч.5 |
Уч.6 |
Уч.7 |
Уч.8 |
Уч.9 |
Уч.10 |
|
1 |
Знаете ли Вы, что такое аликвотные дробй |
Не знаю |
Да, знаю |
Да, знаю |
Да, знаю |
Да, знаю |
Не знаю |
Не знаю |
Да, знаю |
Не знаю |
Да, знаю |
|
2 |
Знаете ли Вы, когда впервые начали использовать аликвотные дроби и где? |
Не знаю |
Да, знаю |
Да, знаю |
Да, знаю |
Да, знаю |
Не знаю |
Не знаю |
Не знаю |
Не знаю |
Не знаю |
|
3 |
Знаете ли Вы, как назывались аликвотные дроби на Русй Например, 1/3; 1/4; 1/6; 1/8… |
Не знаю |
Не знаю |
Да, знаю |
Не знаю |
Да, знаю |
Да, знаю |
Не знаю |
Да, знаю |
Да, знаю |
Не знаю |
|
4 |
Знаете ли Вы, что такое «Глаз Гора»? |
Не знаю |
Не знаю |
Да, знаю |
Не знаю |
Да, знаю |
Да, знаю |
Не знаю |
Не знаю |
Не знаю |
Не знаю |
|
5 |
Знаете ли Вы, что такое аликвотные струны? |
Не знаю |
Не знаю |
Да, знаю |
Да, знаю |
Да, знаю |
Да, знаю |
Не знаю |
Не знаю |
Не знаю |
Не знаю |
|
6 |
Ответ на задачу про 7 хлебов. |
1,5 |
7 |
10 |
7 |
5 |
17 |
Затр. |
56 |
1 |
8 |
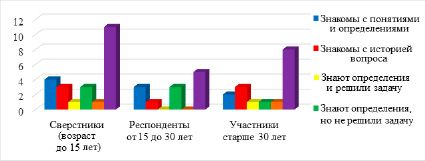
Результат анкетирования:
В анкетировании принимали участие 33 человека:
- сверстники (возраст до 15 лет) – 15 чел.,
- респонденты от 15 до 30 лет – 8 чел.,
- участники старше 30 лет – 10 чел.
На 1-й вопрос 28,13% анкетируемых ответили, что знают аликвотные дроби.
На 2-й вопрос только 21,87% ответило утвердительно, назвав также страну.
18,75% опрошенных дали названия этих дробей правильно.
На 4-й вопрос 12,49% ответили, что знают, о чем идет речь.
По 5-му вопросу 90,62% ответили, что даже не слышали про такие струны.
И 93,75% участников опроса не смогли решить задачу, им потребовалось большее или меньшее количество разрезов, но не 17.
Проанализировав ответы анкетируемых, я сопоставил их с тем, что узнал сам и понял, что надо выступить перед ребятами со своей исследовательской работой и рассказать об этих удивительных дробях и открывающихся перед нами возможностях.
Основная часть
Из истории …
Необходимость в дробных числах появилась очень давно, еще в древние времена… Они понадобились при делении добычи между участниками охоты. В других случаях для измерения разных величин при помощи одной единицы измерения. Как, например, в Древнем Египте, чтобы поделить основную меру объема – «хекат».
Первые дроби, о которых нам известно из истории, это дроби вида – 1/2, 1/3, 1/4 и так далее – так называемые единичные дроби...
Вот несколько названий таких дробей:
• 1/100 – процент
• 1/1000 – промилли
• 1/288 – скрупулус
• 1/24 – семиунция
• 1/8 – сескунция
Эти дроби называли по-разному, но все вместе они назывались аликвотами. В переводе от латинского aliguot – «несколько».
Итак, аликвотными дробями называются дроби вида 1/n, где числитель 1, а n – натуральное число.
Дроби в Древней Греции
В Древней Греции арифметику – учение об общих свойствах чисел – отделяли от логистики – искусства исчисления. Греки считали, что дроби можно использовать только в логистике. Греки очень часто использовали все арифметические действия, производимые с дробями, но не считали их числами. В найденных источниках того времени понятие дроби не встречалось. Ученые в Греции считали, что в математике должны использоваться только целые числа. Они считали, что заниматься дробями могут купцы, ремесленники, астрономы, землемеры, механики и другой «черной люд». «Если ты захочешь делить единицу, математики высмеют тебя и не позволят это делать», – писал основатель афинской академии Платон.
Но в те времена с Платоном соглашались не все древнегреческие математики. Архимед, например, в трактате «Об измерении круга» использует дроби. Герон Александрийский тоже их использовал.
Даже Пифагор, работая над теорией музыкальной шкалы, показал зависимость музыкальных интервалов с дробями, хотя с огромным трепетом относился к натуральным числам. Но если говорить точно, то определением или, скорее, понятием дроби ни Пифагор, ни его ученики не пользовались.
Для дробей вида 1/n использовалась запись: знаменатель дроби сопровождался штрихом справа, числитель не писали. Например, число 32 записывалось как λβ, а дробь 1/32 – λβ’.
«Число» в понимании греков – это набор единиц. Это было недостатком при написании дробного числа. Поэтому сейчас мы используем дробь как единое рациональное число, а греки – как отношение одного целого числа к другому. Вот почему обыкновенные, неединичные дроби практически не встречались в арифметике у греков. Дроби с числителем, равным 1 – именно им отдавалось предпочтение либо же шестидесятеричным дробям.
Дроби на Руси
Первый русский математик, известный нам по имени – монах Новгородского монастыря Кирик, занимался вопросами хронологии и календаря. В его рукописной книге «Учение им же ведати человеку числа всех лет» (1136 г.), т. е. «Наставление, как человеку познать счисление лет» применяется деление часа на пятые, двадцать пятые и т. д. доли, которые он называл «дробными часами» или «часцами».
В VII веке на Руси в писаниях о математике дроби сначала именовались как доли, а позже – «ломаными числами». Слово «дробь» в русском языке впервые упоминалось в VIII веке, это производное от «дробить» – разбивать на части или ломать. Числитель и знаменатель числа разделяла горизонтальная черта.
В старых руководствах есть следующие названия дробей на Руси:
1/2 – половина, полтина
1/3 – треть
1/4 – четь
1/5 – пятина
1/6 – полтреть
1/7 – седьмина
1/8 – полчеть
1/10 – десятина
1/12 –полполтреть
1/16 – полполчеть
На Руси еще применялась земельная мера 1/4 и меньшая – получетверть, ее называли осьмина. Для точного измерения площади земли применялись именно такие дроби, но осьминой непозволительно измерять время или что-то другое. И только позже осьмина стала означать простую дробь 1/8, через которую обозначали абсолютно любую величину.
О том, как использовались дроби на Руси в XVII веке можно прочитать в книге В. Беллюстина «Как постепенно люди дошли до настоящей арифметики»: «В рукописи XVII в. «Статия численная о всяких долях указ «начинается прямо с письменного обозначения дробей и с указания числителя и знаменателя. При произношении дробей заметны особенности: 1/4 называлась четью, доли же со знаменателем от 5 до 11 заканчивались на «ина», так что 1/7 – седмина, 1/5 – пятина, 1/10 – десятина. Нумерация дробей была прямо заимствована из западных источников: числитель назывался верхним числом, знаменатель – исподним».
В 1703 г. выходит в свет первый русский печатный учебник по математике «Арифметика», автора Магницкого Леонтия Филлиповича, в котором в разделе “О числах ломаных или с долями” подробно излагается учение о дробях.
Магницкий в своем учении дает почти современное определение дробям. Он даже более широко, чем нынешние учебники, останавливается на вычислении долей.
На вопрос, что такое ломаное число, Магницкий дает ответ: «Число ломаное не что же иное есть, токмо часть вещи, числом объявленная, сиречь полтина есть половина рубля, а пишется сице 1/2 рубля, или 1/4 рубля, или 1/6 рубля, или 2/5 части и всякие вещи яковые либо часть, объявлена числом, то есть ломаное число».
Магницкий использует название числитель, знаменатель и показывает неправильные дроби, но, кроме всего прочего, выделяет целую часть из неправильной дроби.
Дроби в Древнем Китае
В Китае уже ко II в. до н. э. были описаны почти все известные арифметические операции с обыкновенными дробями. К примеру, в фундаментальном своде математических знаний древнего Китая – «Математике в девяти книгах», окончательная редакция которой принадлежит Чжан Цану. Выделяя наибольший общий делитель в числителе и знаменателе, аналогично тому, что делал Евклид, в Китае сокращали дроби.
Изначально китайцы работали с простейшими дробями, которые получили названия от иероглифа бань:
бань («половина») –1/2;
шао бань («малая половина») –1/3;
тай бань («большая половина») –2/3.
Из древне математики Китая пользовались смешанными числами. Самый ранний трактат о математике «Чжоу би суань цзин» («Канон расчета чжоуского гномона»/«Математический трактат о гномоне»), приводит вычисления возведения в степень различных чисел. Встречается даже 247933/1460.
В «Цзю чжан суань шу» («Правила счета в девяти разделах») дробь – это часть целого, и выражается в n-ном числе его долей – фэнь – m (n < m). Дробь – это «застывший» процесс деления одного числа на другое – делимого на делитель. Дробь всегда меньше единицы. Если в результате деления одного числа на другое получается остаток, то он принимается как числитель дроби, знаменателем которой является делитель. Например, при делении 21 на 5 получается 4 и остаток 1, который дает дробь 1/5.
Дроби в Древнем Египте
Египтяне описывали единичные дроби в древнейших текстах о математике, им более 5000 лет – это древнеегипетские папирусы и вавилонские клинописные таблички.
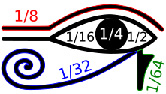
В Древнем Египте составные части Уаджета использовались для обозначения дробей от 1/2 до 1/64, а также применялись для измерений емкостей и объемов.
Сумма всех шести знаков, составляющих «Глаз Гора», если их привести к общему знаменателю, равна: 32/64 + 16/64 + 8/64 + 4/64 + 2/64 + 1/64 = 63/64

|
Иероглиф |
Значение |
Примерная величина |
|
|
часть глаза (справа) |
1/2 (или 32/64) |
|
|
зрачок |
1/4 (или 16/64) |
|
|
бровь |
1/8 (или 8/64) |
|
|
часть глаза (слева) |
1/16 (или 4/64) |
|
|
капля слезы |
1/32 (или 2/64) |
|
|
знак сокола |
1/64 |
|
|
уаджет в сумме |
63/64 |
Для измерения зерновых и сыпучих веществ применялся «хекат», он равнялся примерно 4,785 литрам.
Например:
|
|
|
|
|
|
|
|
|
Хекат ячменя: 1/16 + 1/4 + 1/32 или 11/32 сосуда ячменя.
Египтяне все дроби старались записать как суммы единичных дробей (долей). Например, вместо 8/15 они писали 1/3 + 1/5. Дробь 7/8 записывали в виде долей: 1/2 + 1/4 + 1/8.
Методы использования единичных дробей перенимались одними народами у других. Например, греками от египтян, арабами от греков, а арабы научили Западную Европу считать в дробях. Но выполнять сложение, умножение и деление дробей было очень проблематично и неудобно.
В древние времена решение с помощью обыкновенных дробей нашло наибольшее применение в Индии. Сегодня известны рукописи, датированные примерно IV веком до нашей эры, в которых говорится не только о дробях с числителями равными единице, но с числителями с произвольными значениями. А в начале VII столетия индийцы не только сформулировали правила действий над обыкновенными дробями, но и регулярно их использовали. И только в 1585 году фламандский инженер Симон Стевин представил в Западной Европе понятную и ясную теорию обыкновенных дробей.
Практическая часть
Практическая часть моей исследовательской работы состоит из двух частей анкетирования и экспериментальной – решения задач.
В первой части я проводил анкетирование среди моих друзей и их родителей, а также анализировал его итоги. Во второй – изучал материал, экспериментировал, решая задачи.
Исследование свойств аликвотных дробей
Рассмотрим аликвотные дроби с нечетными знаменателями не больше 100, Приложение № 1.
Дроби с нечетными знаменателями, которые можно представить в виде бесконечной десятичной периодической дроби
Заметим, что в дробях 1/3, 1/5, 1/7, 1/11, 1/13 знаменатели простые числа, и эти дроби можно представить в виде бесконечной десятичной периодической дроби. Найдем произведение этих дробей.
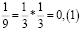
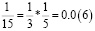
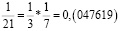
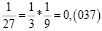
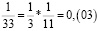
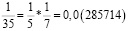
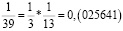
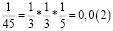
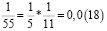
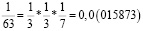
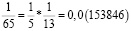
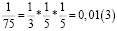
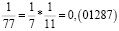
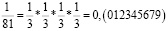
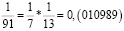
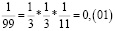
Из аликвотных дробей с нечетными знаменателями меньше 100 я выделил дроби, которые можно представить в виде бесконечной десятичной периодической дроби и заметил, что произведение таких дробей так же представляет собой аликвотную дробь, которую можно представить в виде бесконечной десятичной периодической дроби.
Удивительные свойства дроби 1/7
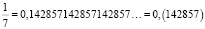
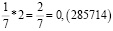
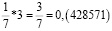
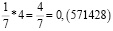
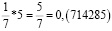
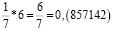
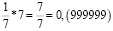
Рассмотрим внимательно первые пять из этих чисел. Заметим, что периоды дробей получаются из первого числа «круговой перестановкой» цифр: сколько-то цифр из конца числа переезжает в начало. Меня удивило то, что если разделить вышеперечисленные числа периодов (кроме последнего) на две части, и найти их сумму, то она будет равна 999. Например: 285 + 714 = 999; 428 + 571 = 999.
С другой стороны, 7 * 1/7 = 1. Делаю вывод: 0,(999999) = 0,(9) = 1
Аликвотные дроби со знаменателями 7n, где n = 1, 2, 4, 8, 16, 32…
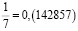
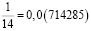
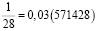
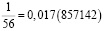
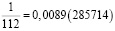
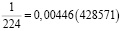
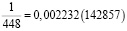
Если внимательно присмотреться, то можно заметить закономерность – в периоде последняя цифра предыдущей дроби переходит в начало следующей дроби.
Аликвотные дроби со знаменателями 2n, где n =1, 2, 3…
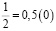
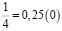
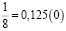
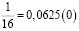
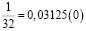
Знаменатели этих дробей являются степенями числа 2, а дробная часть этих чисел (в десятичной записи) является степенями числа 5.
Несколько аликвотных дробей со знаменателями 3, 6, 12, 15
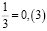
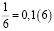
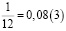
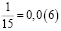
Периоды этих дробей чередуются 3 и 6.
Аликвотные дроби со знаменателями кратные пяти и двум, но не кратные другим нечетным числам
Я обратил внимание, что у всех этих дробей одинаковый период, равный 0.
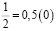
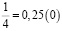
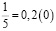
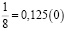
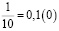
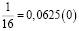
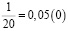
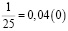
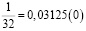
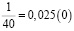
Аликвотные дроби со знаменателями 11n, где n = 1, 2, 3, 4…
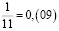
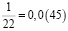
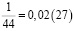
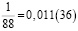
Сумма цифр каждого периода равна 9.
Аликвотные дроби в цвете (Приложение № 2)
Аликвотная дробь 1/9
Умножим аликвотную дробь на целые числа меньше 9 и обратим внимание на цифру в периоде.
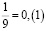
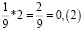
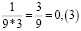
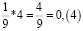
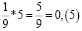
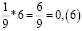
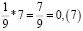
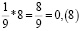
Период полученных дробей равен числу, на которое умножали.
Дробь с числителем равным 2
Для разложения неединичных дробей на сумму единичных существовали готовые таблицы, которыми и пользовались египетские писцы для необходимых вычислений (Именно поэтому папирус Ахмеса начинается с таблицы, в которой все дроби такого вида от 2/5 до 2/99 записаны в виде сумм долей, т.е. в виде суммы двух, трех или четырех аликвот).
Складывать такие дроби было неудобно, т.к. в оба слагаемых могут входить одинаковые доли, и тогда при сложении появится дробь вида 2/n.
А таких дробей египтяне не допускали.
Дроби вида 2/n и 2/(2n + 1) можно записать по формулам:
2/n = 1/n + 1/n,
2/(2n + 1) = 1/(2n +1) + 1/(2n + 1),
или
2/(2n + 1) = 1/(n +1) + 1/(2n + 1)(n +1).
Например,
при n = 2 2/5 = 1/3 + 1/15
при n = 5 2/11 = 1/6 + 1/66 и т.п.
Но, оказалось трудным разложение дроби 2/n на 4 аликвотные дроби. Скажем, число 2/43 выражается так: 2/43 = 1/42 + 1/86 + 1/129 +1/301.
Представление аликвотной дроби вида 1/n в виде суммы двух аликвотных дробей:
Разложить в виде суммы двух аликвотных дробей можно по формуле:
1/n = 1/(n +1) + 1/n(n + 1).
Например, 1/3 = 1/4 + 1/12;
1/5 = 1/6 + 1/30;
1/8 = 1/9 + 1/72.
Разложить в виде разности двух аликвотных дробей можно по формуле:
1/n*(n +1) = 1/n – 1/(n + 1), знаменателями которых являются последовательные числа равные их произведению.
Например: 1/6 = 1/(2 * 3) = 1/2 – 1/3;
1/2 = 1/(1 * 2) = 1/1 – 1/2.
Задачи
№ 1. Представить число 1 в виде сумм различных аликвотных дробей.
а) трех слагаемых:
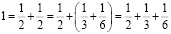
б) четырех слагаемых:
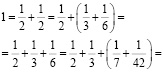
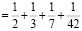
в) пяти слагаемых:
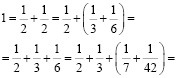
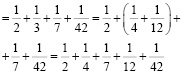
г) шести слагаемых:
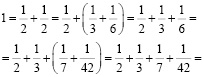
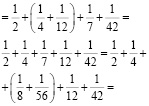
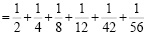
№ 2. Верно ли равенство?
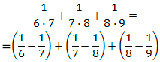

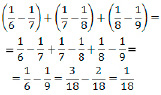
Ответ: Равенство верно.
№ 3. Верно ли равенство?
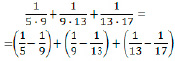
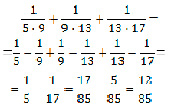
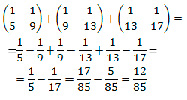
Ответ: Равенство верно.
№ 4. Верно ли равенство?
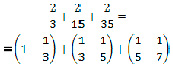
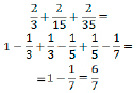
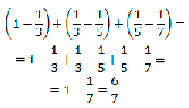
Ответ: Равенство верно.
Олимпиадные задания
№ 5. Найди сумму:
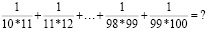
Решение:
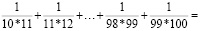
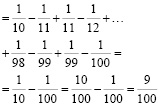
№ 6. Найти сумму:
1/2 + 1/6 + 1/12 + 1/20 + 1/30 + 1/42 + 1/56 + 1/72 + 1/90 = ?
Решение:
1/2 + 1/6 + 1/12 + 1/20 + 1/30 + 1/42 + 1/56 + 1/72 + 1/90 =
= 1/(1*2) + 1/(2*3) + 1/(3*4) + 1/(5*6) + 1/(6*7) + 1/(7*8) + 1/(8*9) + 1/(9*10) = 9/10
Задача № 7. Старинная персидская задача

Персидский крестьянин завещал трем своим сыновьям 17 верблюдов, причем первый должен был получить 1/2 часть всех верблюдов, второй – 1/3 часть, а третий – 1/9. Братья думали долго, но разделить наследство по завещанию отца так и не смогли. Мимо на верблюде проезжал Ходжа Насреддин. Он предложил присоединить к верблюдам еще и своего, и решить таким образом возникшую проблему. И действительно, братья смогли разделить верблюдов так, как наказал отец, причем Ходжа Насреддин получил своего верблюда обратно. Сколько верблюдов досталось каждому сыну?
Решение:
1. 17 + 1 = 18 верблюдов всего;
2. 18 * 1/2 = 9 верблюдов получил первый сын;
3. 18 * 1/3 = 6 верблюдов получил второй сын;
4. 18 * 1/9 = 2 верблюдов получил третий сын;
5. 18 – (9 + 6 + 2) = 1 верблюда вернули Ходже Насреддину.
Ответ: 9, 6, 2 верблюда
Задача № 8

Квадрат со стороной, равной 1, разделили пополам, затем одну его половину опять разделили пополам, одну из получившихся половинок еще раз разделили пополам и т.д. (рис.) Используя рисунок, докажите, что
1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 < 1
На сколько сумма аликвотных дробей, записанных в левой части неравенства, отличается от 1?
Допустим теперь, что сумма в левой части неравенства, построенная по тому же закону, содержит 100 слагаемых. Будет ли неравенство по-прежнему верным?
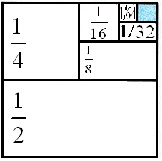
Решение:
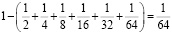
Даже если сумма в левой части неравенства, построенная по тому же закону, содержит 100 слагаемых, неравенство по-прежнему будет верным.
Задача № 9
Представьте в виде суммы аликвотных дробей следующую дробь:
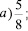
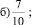
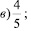
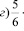
Решение:
а) 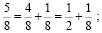
б) 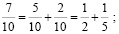
в) 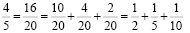
г) 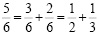
Задача № 10
Используя аликвотные дроби, покажите, как можно разделить три яблока между четырьмя людьми, не разрезая каждое на 4 части.
Решение:
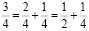
- значит, два яблока надо разрезать на 2 части, а одно яблоко – на 4 части.
Ответ: Каждому человеку достанется по половине и четверти яблока.
Задача № 11
Рассмотрите равенства:
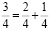
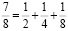
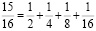
Подметьте закономерность и «сконструируйте» следующее равенство. Проверьте себя, выполнив сложение дробей.
Решение:
Рассмотрим внимательно суммы аликвотных дробей:
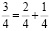
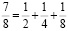

Знаменатели аликвотных дробей представляют собой степени числа 2: 2 = 21,
4 = 22, 8 = 23 ,16 = 24. Легко заметить, что следующий знаменатель 32 = 25.
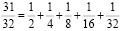
Ответ:
Задача № 12
Найдите значение суммы
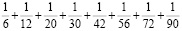
заменив каждое слагаемое разностью аликвотных дробей:
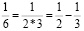
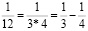
Решение:
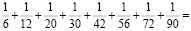
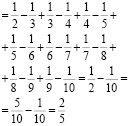
Ответ:
Задача № 13
Используя прием представления дробей в виде разности вычислите:
а) 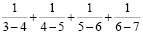
Решение:
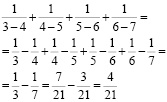
б) 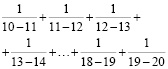
Решение:
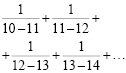
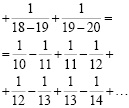
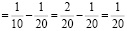
в) 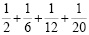
Решение:
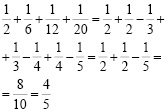
г) 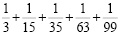
Решение:
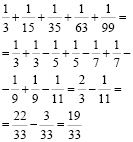
Задача № 14
Не выполняя сложения дробей, объясните, почему верно неравенство:
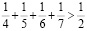
Решение:
Чтобы доказать это равенство я воспользовался кубиками из «Дома дробей».
На картинке видно, что длина дроби 1/2 меньше 1/4 + 1/5 + 1/6 + 1/7

Приложение 1
Запись аликвотных дробей в виде десятичных



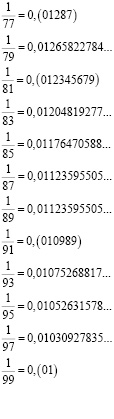
Приложение 2
Аликвотные дроби в цвете
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
продолжение табл. |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,00714285714285… |
|
|
|
0.06666 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,05263157894. |
|
|
|
|
|
|
0,047619047619… |
|
|
|
|
|
|
окончание табл. |
||
|
|
|
0,04347826086.. |
|
|
|
|
|
|
|
|
Голубой цвет – период дроби равен нулю
Красный цвет – бесконечная десятичная периодическая дробь
Светло-розовый цвет – одна цифра в периоде
Желтый цвет – 6 цифр в периоде
Фиолетовый цвет – 2 цифры в периоде
Приложение 3
Высказывания о дробях
До сих пор бытует мнение, что учение о дробях всегда оставалось труднейшим разделом арифметики, но в то же время в любую из предшествующих эпох люди сознавали важность изучения дробей, и учителя в стихах и прозе старались приободрить своих учеников.
* * *
Л.Магницкий писал:
Но несть той арифметик,
Ижо в целых ответчик,
А в долях сий ничтоже,
Отвещати возможе.
емже о ты радеяй,
Буди в частях умеяй.
* * *
«Он дальше десятичных дробей вряд ли ходил»
П. Боборыкин
* * *
«Без знаний дробей никто не может признаваться знающим арифметику»
Цицерон
* * *
Автор старинной славянской рукописи 16 века пишет: «Не есть се диво, что…в целых, но есть похвально, что в долях…»
Кто знал дроби, был в почете.
Заключение
Я узнал очень много нового из прочитанного, теперь мои знания еще и подкрепились проведенной экспериментальной работой по решению и разбору конкретных задач. Мне есть чем поделиться с друзьями, я обязательно составлю презентацию и выступлю перед одноклассниками.
Выводы
Разобрав весь этот материал и интереснейшие задачи, я выявил следующее:
– первыми дробями, которыми оперировали люди, были аликвотные дроби; причем, эти дроби с числителем 1 долгое время были единственными, которыми как-то умел пользоваться человек;
– задачи с использованием аликвотных дробей составляют обширный класс нестандартных задач;
– решив проблему разложения аликвотных дробей на две аликвотные дроби, мы пришли к выводу, что разложение на три, четыре, пять и т.д. аликвотных дробей можно произвести, разложив одно из слагаемых на две дроби, следующее слагаемое еще на две аликвотные дроби и т.д.;
– аликвотные дроби используются тогда, когда требуется что-то разделить на несколько частей с наименьшим количеством действий для этого;
– разложение дробей на две аликвотные дроби систематизированы в виде формулы, преобразовав которую, легко можно решать олимпиадные задачи по математике;
– путем вычислений и анализа бесконечных периодических дробей я смог показать, что аликвотные дроби можно разбить на группы, обладающими определенными свойствами.
За время работы над этой темой я исследовал только самые основные понятия и некоторые способы решения задач. Они обладают достоинствами, которые позволяют использовать их для развития сообразительности и улучшения логического мышления.
Проанализировав свои исследования, можно заключить:
1. Значительно расширены знания о периодических и аликвотных дробях.
2. Найдены свойства аликвотных дробей.
3. Практическая значимость работы достигнута.
4. Решены задачи на применение аликвотных дробей.
5. Сформулирован вывод. Доказана гипотеза.
Итак, из всего вышесказанного неопровержимо следует практическая ценность аликвотных дробей и их свойств. И, как следствие, проведенных исследований и изучения основных свойств, напрашивается вывод, что группы аликвотных дробей обладают одинаковыми свойствами. Что в свою очередь доказывает нашу гипотезу – от обратного, что и являлось целью данной работы, т.е. проблема исследования решена.
Но заканчивая это исследование, я не планирую останавливаться на достигнутом. Меня очень заинтересовала тема дробей. Поэтому продолжением ее станет новое исследование.
А этот материал, думаю, будет интересным и практически полезным моим любознательным друзьям и одноклассникам.
Я убедился в том, что математика и логика очень затягивают. Я научился анализировать, выдвигать гипотезы, использовать логику, делать выводы.
Мне очень понравилось решать сложные задачи самому.
А вообще, порой и не представляешь, сколько интересного вокруг тебя. Нужно только оглянуться, обратить внимание, а затем провести исследование и ответить на интересующие вопросы.
Итак, начало положено, теперь вперед!
Библиографическая ссылка
Фесенко С.А. АЛИКВОТНЫЕ ДРОБИ // Международный школьный научный вестник. 2018. № 5-5. ;URL: https://school-herald.ru/ru/article/view?id=746 (дата обращения: 13.02.2026).









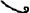
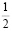
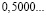
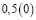
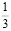
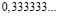
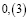
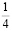
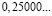
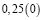
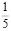
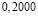 …
…
 …
…
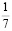
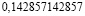
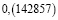
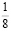
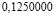 …
…