Данная статья является реферативным изложением основной работы. Полный текст научной работы, приложения, иллюстрации и иные дополнительные материалы доступны на сайте II Международного конкурса научно-исследовательских и творческих работ учащихся «Старт в науке» по ссылке: https://www.school-science.ru/2017/7/27328.
Рассказывают, что Николай I перед строительством железной дороги из Санкт-Петербурга в Москву положил на карту линейку и провёл карандашом прямую линию между этими двумя столицами Российской империи. В районе Валдайской возвышенности карандаш наскочил на палец императора, и в этом месте дорога сделала небольшой крюк.
А вот ещё один «комичный» факт, но уже не исторический, а наших дней. Один человек сдавал в бухгалтерию отчёт о командировке, в котором цена железнодорожного билета из Москвы в Петербург была несколько выше цены обратного билета. На вопрос бухгалтера, откуда взялась такая разница, подотчётное лицо посоветовало посмотреть на … глобус: из Москвы в Петербург поезд поднимается вверх к Северному полюсу, а на обратном пути катится под горку к экватору…
Николай I для ещё большего сокращения пути должен был не просто прочертить карандашом прямую линию на карте, а … просверлить в глобусе прямое отверстие, соединяющее Москву с Петербургом!
Шутки шутками, но уже давно обсуждается полуфантастический проект так называемого гравитационного поезда, катящегося без трения на магнитной подвеске в прямолинейном подземном туннеле, из которого выкачан воздух.
Первую половину пути гравитационный поезд будет катиться под горку без какой-либо тяги локомотива, а вторую половину пути будет подниматься вверх, замедляясь без тормозов до самого пункта назначения, где он и остановится.
В Интернете есть множество готовых формул, по которым можно оценить, сколько времени такой поезд будет в пути и какой максимальной скорости он достигнет в середине туннеля.
В данной работе рассмотрим решение задачи о гравитационном поезде, двигающемся в подземном прямолинейном туннеле с силами трения и без них, но вычисления произведём не по формулам, а проанализируем баланс сил, действующих на гравитационный поезд, составим уравнение (функцию) положения поезда в туннеле в зависимости от времени, и решим его среде Mathcad.
Тема исследовательской работы: «Путешествие из Петербурга в Москву или Свет в конце туннеля».
Гипотеза: пункты планеты Земля можно соединить подземным туннелем, передвигаться по которому можно с огромной скоростью.
Цель: рассмотреть решение задачи о гравитационном поезде, двигающемся в подземном прямолинейном туннеле.
Задачи:
1. Рассмотреть понятие модели гравитационного поезда.
2. Проанализировать баланс сил, действующих на гравитационный поезд.
3. Составить уравнение движения поезда в туннеле в зависимости от времени.
4. Провести численный эксперимент в среде Mathcad по нахождению времени и скорости движения гравитационного поезда по прямолинейному туннелю.
5. Теоретически проанализировать создание туннеля для гравитационного поезда.
Объект исследования: гравитационный поезд.
Предмет исследования: нахождение времени и скорости (максимальной и минимальной) движения гравитационного поезда по прямолинейному туннелю в среде Mathcad.
Методы: работа с литературным источником, вычисления в программе Mathcad, поиск, изучение, анализ, обобщение, сравнение.
Практическая значимость: решение задачи о гравитационном поезде с помощью дифференциального уравнения .
Актуальность работы заключается в том, что отказ от вычислений движения гравитационного поезда по формулам, позволит усложнить модель, приблизить её к реальности, учтя силы трения.
Теоретическая часть
Гравитационный поезд – теоретическое средство транспортировки, разработанное таким образом, чтобы перемещаться между двумя пунктами на поверхности сферического объекта посредством прямого туннеля, который проходит непосредственно от одного пункта до другого через этот самый объект.
Mathcad – уникальный математический пакет, компьютерное программное обеспечение для работы с уравнениями, числами, текстом и графиками.
Дифференциальное уравнение – уравнение, связывающее значение производной функции с самой функцией, значениями независимой переменной, числами (параметрами). Производные, функции, независимые переменные и параметры могут входить в уравнение в различных комбинациях или все, кроме хотя бы одной производной, отсутствовать вовсе.
Обыкновенное дифференциальное уравнение – это дифференциальное уравнение для функции от одной переменой. Классическим решением дифференциального уравнения называется n раз дифференцируемая функция, удовлетворяющая уравнению во всех точках своей области определения.
Понятие модели гравитационного поезда
В большом теле, таком как планета, гравитационный поезд можно было бы приводить в движение, используя только силу тяжести. В начале, во время первой половины поездки (от пункта отправления до середины), сила тяжести будет двигать его к месту назначения. Во время второй половины поездки ускорение свободного падения было бы в противоположном направлении относительно траектории, однако (игнорируя силу трения) скорости, приобретенной прежде (в первой половине путешествия) будет достаточно, чтобы поезд достиг своего места назначения со скоростью равной нулю. Время в пути всех гравитационных поездов на выбранной планете будет одинаковым независимо от пункта назначения и места отбытия. Для Земли это время равнялось бы 2530.30 секундам (почти 42.2 минуты), в том случае если земля являлась бы идеальной сферой.
Время поездки зависит только от плотности планеты и гравитационной постоянной. Максимальная скорость достигается в середине путешествия. Для поезда, который идет непосредственно через центр Земли, эта максимальная скорость составляет приблизительно 7 900 метров в секунду.
Понятие прямолинейного туннеля
Фундаментальное понятие, связанное с поездом гравитации, является прямой туннель. Если бы поезд в одном конце туннеля затормозил, сила гравитации заставляла бы поезд ускоряться. Более крутые наклоны привели бы к большему значению скорости, с самым высоким ускорением, встречающимся в прямых туннелях, которые пересекают центр Земли. Поезд продолжил бы ускоряться до достижения лежащей на полпути точки, в которой значение инерции будет меньше гравитации, а затем бы, начал бы замедлять движение.
Самое большое техническое препятствие в реализации этой идеи заключается в создании массивных туннелей. Мантия Земли и ядро имеют большое давлением и высокую температуру. К сожалению никакие в настоящее время известные материалы не могут даже противостоять окружающей среде, уже не говоря об изолировании туннеля от высокой температуры. Из-за этих чрезвычайных температур, в поезде невозможно находится людям. Но технология была бы чрезвычайно полезной для быстрой, беспилотной грузовой поставки между континентами.
Рассмотрим прямой туннель между двумя пунктами планеты. Из рисунка видно, что туннель понижается от одного пункта до середины, а затем до второго. Конечно «внизу» туннель ближе к центру Земли, сила гравитации направлена прямо к центру.
Теперь проложим железную дорогу в туннеле. Как только тормоза поезда по железной дороги в первом пункте выпущены, поезд будет катиться вниз под силой гравитации. Именно эта сила ускоряет поезд, в середине туннеля он достигнет максимальной скорости, а затем будет двигаться замедленно, так как повышается инерция. Если мы пренебрежем потерей энергии для трения, то Закон Сохранения Энергии будет подразумевать, что поезд достигнет второго только тогда, когда его скорость станет равной нулю.
Для целого путешествия не потрачено ни капли топлива. Все меры должны быть приняты, конечно, чтобы уменьшить трение в максимально возможной степени. Для этого, например, нужно откачать воздух от туннеля. Чтобы давать компенсацию за остающееся трение между рельсом и колесами, можно использовать очень маленький двигатель.
Вывод: топливная эффективность при движении по туннелю гравитационного поезда намного выше, чем для авиалиний, или даже для судов.
Выводы
Для быстрого передвижения между двумя пунктами планеты Земля можно использовать гравитационный поезд, двигающийся в подземном прямолинейном туннеле. Время движения на данном поезде не зависит от выбора пунктов отправления и назначения и всегда на планете Земля равно 42 минутам, топливная эффективность данного передвижения ничтожно мала.
Для решения задачи о движении гравитационного поезда между городами Петербург – Москва будем использовать математическую программу Mathcad.
В данной работе «фантастический» туннель строился по прямой линии, соединяя два пункта планеты Земля. А по какой траектории строятся «реальные» туннели, если нет никаких ограничений?!
Ответ 1: «По прямой линии» (как и в данной работе). Но в «прямом» туннеле будет скапливаться вода, и ее нужно будет непрерывно откачивать. Рисунок 9 можно интерпретировать и как график, описывающий перетекание лужи воды, вылитой у входа в прямолинейный туннель, где тяга локомотива заменена тягой ветра в туннеле.
Ответ 2: «По дуге окружности». Дугообразный же туннель, повторяющий окружность Земли, копать довольно сложно.
Горные туннели обычно строят так: из двух точек, расположенных на противоположных склонах гор, два проходческих щита, управляемые, лазером начинают прокладывать туннель строго по прямой линии. Сама же трасса каждой строящейся половинки туннеля несколько поднимается над уровнем горизонта. Проходческие щиты должны встретиться в центре туннеля несколько выше стартовых точек. В таком построенном крышеобразном туннеле не только не будет скапливаться вода, но и при необходимости из него за счет своего веса сможет выкатиться заглохший транспорт. Свет в конце такого туннеля можно увидеть, только дойдя до его середины…
Подводные же туннели, например, туннель под Ламаншем, строятся, конечно по более сложным траекториям.
Вывод: туннель для гравитационного поезда должен быть прямолинейным, в противном случае возникают проблемы движения «вперёд» до пункта назначения (в центре дугообразного туннеля поезд будет «катиться» назад). А так как основной идеей гравитационного поезда являются минимальные затраты энергии (и движение, и видимость в конце туннеля), то модели с траекториями, отличными от прямой стали неактуальными.
Заключение
Рассмотрев понятие модели гравитационного поезда и проанализировав баланс сил, действующих на гравитационный поезд, было составлено дифференциальное уравнение движения поезда в туннеле в зависимости от времени:
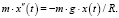
И теоретически, и нашим численным экспериментом в работе было доказано, что время движения гравитационного поезда не зависит от длины туннеля и равно этим самым 42 минутам, которые можно считать некоей константой, характеризующей нашу планету и связанной с гравитационной постоянной и плотностью Земли. При иных длинах туннеля будет меняться только скорость поезда – средняя и максимальная. В туннеле Москва – Петербург средняя скорость равна 857 км/ч.
Несложно подсчитать, что если железную дорогу между Москвой и Петербургом длинной в 600 км проложить не на поверхности Земли (по поверхности идеального шара с радиусом 6400 км), а в туннеле строго по прямой, то расстояние между этими двумя городами сократилось бы всего лишь на 220 м.
Отказ от готовых формул позволил нам усложнить нашу математическую модель гравитационного поезда, приблизив ее к реальности через учет сил трения.
В реальности, есть две причины, по которым гравитационные поезда не существуют. Первая заключается в том, что никакие известные в настоящее время материалы не способны противостоять очень высокой температуре и давлению земных недр. Вторая проблема – это трение. Проблема трения качения могла бы быть решена с помощью маглева. Однако, если весь воздух не будет выкачан из туннеля, возникает проблема сопротивления воздуха.
Задача на будущее: решение проблемы трения качения, требующей дополнительных решений и мощностей.
И последнее. Послесловие.
Палец Николая I на линии «Москва-Петербург» это не просто исторический анекдот. Это объезд реальным поездом реального большого и глубокого оврага, поперек которого проложили насыпь и мост только в 2000 г. при реконструкции дороги.
Библиографическая ссылка
Нечаева Л.В. ПУТЕШЕСТВИЕ ИЗ ПЕТЕРБУРГА В МОСКВУ ИЛИ СВЕТ В КОНЦЕ ТУННЕЛЯ // Международный школьный научный вестник. 2016. № 3. ;URL: https://school-herald.ru/ru/article/view?id=78 (дата обращения: 31.08.2025).
