Тригонометрия – раздел математики, в котором изучаются тригонометрические функции и их приложения к геометрии. Слово тригонометрия состоит из двух греческих слов: «trigwnon» – «треугольник» и «metrew» – «измерять», означает – «измерение треугольников». Именно эта задача – «измерение треугольников» или «решение треугольников», определение всех элементов треугольника по трем данным, с древнейших времен составила основу практических приложений тригонометрии.
Актуальность: знакомство с новым предметом – тригонометрией.
Цель: Расширить знания по истории развития тригонометрии.
Задачи:
1. Чем вызвана к жизни наука тригонометрия
2. Применение тригонометрии в астрономии, физике, биологии и медицине.
Объект: тригонометрия, история зарождения и развития тригонометрии.
Гипотеза: многие физические явления природы можно описать с помощью тригонометрии.
Новизна: знакомство с тригонометрией.
Методика исследования. Изучение литературы по данной теме, информации из Интернет-ресурсов. Обобщение найденного материала.
Продукт: Буклет «История тригонометрии».
Практическая значимость: данный материал можно использовать на уроках геометрии и тригонометрии для дополнительного образования. Любой ученик может развить в себе интерес к науке тригонометрии через данный материал.
Возникновение тригонометрии
Исторически тригонометрия сложилась из задач на решение плоских и сферических треугольников.
Как и всякая другая наука, тригонометрия возникла в результате человеческой практики в процессе решения конкретных практических задач.
Возникновение тригонометрии тесно связано с развитием одной из древнейших наук – астрономии. Главная роль принадлежит ей в формировании и развитии сферической тригонометрии. Со времен древнего Вавилона до времени Эйлера и Лапласа астрономия была руководящей и вдохновляющей силой самых замечательных математических открытий.
Развитие астрономии, вызвано, в первую очередь, необходимостью составления правильного календаря, имевшего важное значение для земледельческого хозяйства древности. Земледельцу нужно было знать смену времен года, чтобы своевременно производить необходимые сельскохозяйственные работы. Календарь был необходим также и служителям культа, исполняющим религиозные обряды, для определения дней праздником и многим другим лицам.
Развитие торговли, связанное с необходимостью передвижения, как по суше, так и водным путем, оказало большое влияние на развитие астрономии: нужно было уметь правильно определять курс корабля в открытом море.
Значительную роль в развитии астрономии и связанной с ней тригонометрии сыграла, несомненно, потребность в составлении точных географических карт, это требовало правильного определения больших расстояний на земной поверхности.
Врачам нужна была астрономия, алгебра и тригонометрия для астрологических вычислений, чтобы составить гороскоп больного и по расположению планет в созвездиях определить, поправится больной или нет.
Эти и другие стороны деятельности человека уже в глубокой древности наталкивались на необходимость ознакомления с положением и видимым движением небесных светил (Солнца, Луны, звезд).
Уровень развития математики у древних народов Двуречья был более высоким, чем у других восточных народов. У древних народов Двуречья были особенно развиты астрономические наблюдения. Следовательно, они владели некоторыми простейшими сведениями из тригонометрии. Уже 2-3 тысяч лет до нашей эры древние египтяне практически использовали астрономические наблюдения при работах по сельскому хозяйству. Разливы Нила были важны фактором в развитии земледелия.
В классическом китайском трактате «математика в девяти книгах», составленном во II-I веках нашей эры по более ранним источникам, в книге IX трактата собран ряд задач на применение прямоугольных треугольников, где есть задачи на определение расстояния до недоступных предметов. Больших успехов в астрономии добились древние майя, ими был создан достаточно точный календарь (календарно-хронологическая система).
Тригонометрия в Древней Греции
Значительно позднее тригонометрия вступила в следующий этап своего развития в древней Греции, как часть астрономии. В связи с потребностями астрономии и геодезии первостепенное значение получили вычислительные задачи сферической тригонометрии. Некоторое знакомство с сферической тригонометрией имел еще Фалес Милетский (640 – 548 гг. до н.э. – древнегреческий математик и астроном (Приложение 1); в первой половине 3 веке до н.э. древнегреческий астроном и математик Аристарх Самосский (310 – 230 г г. до н.э.); Архимед (Приложение 1), высказал смелую гипотезу о том, что Земля движется по кругу около Солнца (за это его обвинили в безбожии и изгнали из Афин).
Уже в середине I тысячелетия до н.э. древнегреческие ученные знали, что Земля имеет форму шара, в частности длины его окружности. Были разработаны некоторые методы решения этой задачи. Первое измерение дуги меридиана и радиуса Земли принадлежит Эратосфену Киренскому (ок. 276 – 194 гг. до н.э.) – древнегреческому математику, географу, историку, философу, поэту (Приложение 1).
Но основополагающее значение для развития тригонометрии в эпоху ее зарождения имели работы древнегреческого ученого Гиппарха (ок. 180 – 125 г г. до н.э. ) (Приложение 1) – основателя научной астрономии.
Гиппарх составил звездный каталог с тем, чтобы будущие астрономы могли следить за появлением новых звезд и исчезновением старых. В каталог было занесено положение на небе более 1 тысячи звезд, подразделенных им по блеску на 6 звездных величин и определенных им по блеску на 6 звездных величин и определенных для того времени весьма точно. Гиппарх явился основоположником математической географии. Им было введено определение точек на земной поверхности при помощи географических координат – широты и долготы.
Важно отметить, что тригонометрии как науки в современном смысле этого слова не было ни у Гиппарха, ни у других ученных древности. Но они, пользуясь известными им положениями элементарной геометрии, решали те задачи, которые сейчас относятся к тригонометрии. В основе всех тригонометрических вычислений у греков лежала известная еще Гиппарху теорема Птолемея, которую можно сформулировать так: «Произведение диагоналей вписанного в круг четырехугольника равно сумме произведений противоположных сторон».
Тригонометрия в Индии
Следующий шаг по развитию тригонометрии связан с развитием математической культуры народов индии с IV по XII вв. Наряду с «синусом» индийцы ввели в тригонометрию «косинус», точнее говоря, стали употреблять в своих вычислениях линию косинуса. Сам термин «косинус» появился значительно позднее в работах европейских ученных австрийского математика Пейрбаха или Пурбаха (1423 – 1461) и немецкого математика Региомонтана (1436 – 1476) .) (Приложение 1).
Индийцам было так же известно соотношение sin2a + cos2a= r2 , а также формулы для синуса половинного угла и синуса суммы и разности двух углов. Таким образом, индийцы положили начало тригонометрии как учению о тригонометрических величинах, хотя у них и было мало внимания отведено как раз решению треугольников. Для измерений высот и расстояний были разработаны несколько правил, основанных на изменении тени вертикального шеста – гномона и на подобии треугольников. Все это предвосхищало введение тангенса и котангенса.
Тригонометрия в странах Арабского Халифата
Следующий этап в развитии тригонометрии связан с расцветом культуры стран арабского халифата. Так называлось объединение различных стран и народов, завоеванных арабами в VII – VIII вв. в него входили таджики, узбеки, персы, азербайджанцы, египтяне, сирийцы и другие народы. Многие из этих народов стояли на более высоком уровне общественного и культурного развития, чем сами арабы. Необходимые сведения по астрономии вместе с тригонометрией, алгеброй и арифметикой были заимствованы в первые из Индии. И хотя индийская математика дала начало развитию арабской математики, господствующее положение в нарождающейся науки науке у арабов занимала греческая геометрия и астрономия, благодаря переводом всех трудов Евклида, Аполлония, Архимеда, Птолемея и их позднейших комментаторов. Особенно велик вклад, внесенный арабоязычными народами в математику. Это прежде всего десятичная система счисления, позаимствованная арабами у индийцев и позже, благодаря трудам арабоязычных ученых, получившая распространение в Европе. Успехи в математике, в частности в тригонометрии, создали основу для достижений в астрономии и в некоторых других науках.
Тригонометрия и здесь развивалась в тесной связи с астрономией и географией и носила ярко выраженный «вычислительный» характер.
В Багдаде в разное время занимались научной работой такие ученые, как ал – Хорезми (783 – 830), ал – Хабаш (764 – 874), Ибн кора (836 – 901), Ибн Ирак (965 – 1035), ал – Бируни (973 – 1050) (Приложение 1) .)
Ал – Хорезми внес большой вклад в развитии математики, астрономии и математической географии. Его труды в течение нескольких столетий оказывали сильное влияние на ученных Востока и Запада и долго служили образцом при написании учебников математики. Два его трактата по арифметики и алгебре сыграли большую роль в развитии математики.
Тригонометрия в Европе
В XII вв Европе возникает городская культура, развиваются товарно–денежные отношения внутри феодальной системы хозяйства. Этому способствовали также торговые путешествия и крестовые походы, позволившие частично познакомиться не только с движениями восточной культуры, но и с культурой древней Греции. Начинается самостоятельное творчество европейских ученых. Им пришлось заново открывать многое из того, что открыто было задолго до них. Первые их достижения относятся именно к тригонометрии. Эта наука разливалась в основном на базе достижений древних греков. Появились переводы некоторых «арабских» сочинений по тригонометрии. На основе этих сочинений в Англии были написаны работы по тригонометрии Р. Уоллигрфордом (ок. 1292 – 1335) и его современником Д. Модюктом. Английский ученый Томас Брадвардин (ок. 1290 – 1349) (Приложение 1). Он впервые в Европе предложил единичный радиус тригонометрического круга, ввел в тригонометрические вычисления котангенс под назначением «прямой тени» и тангенс под названием «обратной тени». В этот период составляют таблицы синусов.
Региомонтан, независимо от арабов (опередивших его на 400 лет) и Т.Бродвардина, ввел в еврейскую науку функцию тангенса, составил таблицу синусов через 1’ и таблицу тангенсов через 1о . он составил так же таблицу для вычисления катета прямоугольного треугольника (сферического ) по лежащему против него углу А и по гипотенузе С согласно формуле sina – sinCsinA,назвав ее таблицей «с двойным входом». Эта работа Региомонтана (Приложение 1) сыграла очень большую роль в дальнейшем развитии тригонометрии.
Важный вклад в развитие тригонометрии внес польский астроном Николай Коперник (1473 – 1543) (Приложение 1), создатель гелиоцентрической системы мира, реформатор астрономии. Не знакомый с работами Региомонтана, Коперник самостоятельно обосновал некоторые основные положения сферической тригонометрии; он впервые сводит все дело к трехграннику, проектирующему треугольник из центра. Коперник сам занимался составлением тригонометрических таблиц. Немецкий математик Петер Крюгер (1480 – 1532) был первым из европейских математиков, составивших отдельно таблицы логарифмов тригонометрических функций и таблицы логарифмов чисел. Датский математик Томас Финк (1561 – 1656) (Приложение 1) в работе «Геометрия круглого»(1583) впервые вводит термины «синус», «тангенс» и «секанс».
Английский математик Абрахам Муавр (1667 – 1754) (Приложение 1), по происхождению француз, находит правило для возведения в степень комплексного числа, заданного в тригонометрической форме, которое широко применяется в тригонометрии и алгебре при решении двухчленных уравнений и известно теперь как «формула Муавра».
В настоящее время тригонометрия перестала существовать как самостоятельная наука, распавшись на две части. Одна из этих частей представляет собой учение о тригонометрических функциях, а другая – вычисление элементов тригонометрических фигур.
Первая часть, как мы уже говорили выше, входит в состав математического анализа, располагающего общими методами исследования функций, а вторая часть относится к геометрии и играет в ней вспомогательную роль.
«Геометрическая» часть тригонометрии в свою очередь распадается на два раздела – «прямолинейную тригонометрию» и «сферическую тригонометрию». Основным содержанием первого раздела является вычисление элементов плоских треугольников, а второго раздела – вычисления элементов сферического треугольника.
Применение тригонометрии
Продолжая тему тригонометрии важно отметить, что тригонометрические вычисления применяются практически во всех сферах жизнедеятельности людей: астрономии, физике, природе, музыке, медицине, биологии и многих других.
Тригонометрия в астрономии
Так в астрономии возникла потребность в «решении треугольников».
Составленные Гиппархом таблицы положений Солнца и Луны позволили предвычислять моменты наступления затмений (с ошибкой 1–2 ч). Гиппарх впервые стал использовать в астрономии методы сферической тригонометрии.
Тригонометрия в физике
В окружающем нас мире приходится сталкиваться с периодическими процессами, которые повторяются через одинаковые промежутки времени. Эти процессы называются колебательными. Колебательные явления различной физической природы подчиняются общим закономерностям и описываются одинаковыми уравнениями. Существуют разные виды колебательных явлений.
Механические колебания. Механическими колебаниями называют движения тел, повторяющиеся точно через одинаковые промежутки времени. Графическое изображение этой функции дает наглядное представление о протекании колебательного процесса во времени. Примерами простых механических колебательных систем могут служить груз на пружине или математический маятник.
Тригонометрия в природе
Впервые теория радуги была дана в 1637 году Рене Декартом. Он объяснил радугу, как явление, связанное с отражением и преломлением света в дождевых каплях.
Северное сияние Проникновение в верхние слои атмосферы планет заряженных частиц солнечного ветра определяется взаимодействием магнитного поля планеты с солнечным ветром.
Сила, действующая на движущуюся в магнитном поле заряженную частицу называется силой Лоренца. Она пропорциональна заряду частицы и векторному произведению поля и скорости движения частицы.
Тригонометрия в медицине
Ученые утверждают, что мозг оценивает расстояние до объектов, измеряя угол между плоскостью земли и плоскостью зрения.
К тому же в биологии используется такое понятие как синус сонный, синус каротидный и венозный или пещеристый синус.
Тригонометрия играет важную роль в медицине. С ее помощью иранские ученые открыли формулу сердца – комплексное алгебраически-тригонометрическое равенство, состоящее из 8 выражений, 32 коэффициентов и 33 основных параметров, включая несколько дополнительных для расчетов в случаях аритмии.
Тригонометрия и тригонометрические функции в медицине и биологии, музыке
Одно из фундаментальных свойств живой природы – это цикличность большинства происходящих в ней процессов. Биологические ритмы, биоритмы – это более или менее регулярные изменения характера и интенсивности биологических процессов. Основной земной ритм – суточный. Модель биоритмов можно построить с помощью тригонометрических функций.
Тригонометрия играет важную роль в медицине. С ее помощью иранские ученые открыли формулу сердца – комплексное алгебраически-тригонометрическое равенство, состоящее из 8 выражений, 32 коэффициентов и 33 основных параметров, включая несколько дополнительных для расчетов в случаях аритмии.
Биологические ритмы, биоритмы связаны с тригонометрией. Модель биоритмов можно построить с помощью графиков тригонометрических функций. Для этого необходимо ввести дату рождения человека (день, месяц, год ) и длительность прогноза.
Движение рыб в воде происходит по закону синуса или косинуса, если зафиксировать точку на хвосте, а потом рассмотреть траекторию движения.
При полёте птицы траектория взмаха крыльев образует синусоиду.
Частоты, соответствующие одной и той же ноте в первой, второй и т.д. октавах, относятся, как 1:2:4:8…
диатоническая гамма 2:3:5
Заключение
В ходе исследовательской работы расширились знания по тригонометрии, изучены материалы по истории тригонометрии и сделан вывод о том, что тригонометрия была вызвана к жизни необходимостью производить измерения углов, но со временем развилась и в науку о тригонометрических функциях.
Выяснили, что тригонометрия исторически сложившаяся наука. Она была вызвана к жизни необходимостью производить измерения углов, но со временем развилась и в науку о тригонометрических функциях.
Убедились, что тригонометрия перестала существовать как самостоятельная наука, распавшись на две части.
Думаем, что тригонометрия не только нашла своё применение в жизни человека, что сферы применения её будут расширяться.
Приложение 1
Ученые, внёсшие вклад в развитие тригонометрии

Фалес Милетский

Аристарх Самосский

Архимед

Виета

Эратосфен Киренский


Гиппарх

Пейрбах

Региомонтана

Томас Брадвардин

Хорезми

Ибн кора

ал – Бируни

Николай Коперник


Томас Финке

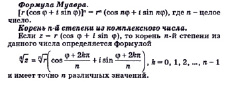
Абрахам Муавр
Библиографическая ссылка
Павлова П.А. ИСТОРИЯ ТРИГОНОМЕТРИИ // Международный школьный научный вестник. 2018. № 6-1. ;URL: https://school-herald.ru/ru/article/view?id=804 (дата обращения: 10.02.2026).
