«Расскажи, и я забуду.
Покажи, и я запомню.
Дай попробовать, и я пойму».
Древняя китайская мудрость
В «топ» самых частых ошибок в ЕГЭ входит неправильное чтение графиков. Экзаменаторы отмечают, что ученики не понимают условие задания, допускают простейшие арифметические ошибки и не умеют себя проверить – все это, естественно, очень негативно влияет на результат.
Анализ результатов ЕГЭ по математике 2017-2018 года в МБОУ «Лицей № 9 им. К.Э. Циолковского» г. Калуги показал, в частности, что задание № 7 выполнили 61,24 % всех экзаменующихся, а задание № 18 – 4,08 %.
Итак, на лицо проблема: как простое задание № 7, так и сложное, № 18, вызывает у экзаменующихся затруднения.
Задачи, предлагаемые в задачнике «Алгебра и начала математического анализа 10 класс. Профильный уровень. Часть 2 » А.Г. Мордкович и др. Москва, «Мнемозина», 2010, которые можно отнести к № 7 – это № 40.5-№ 40.8. Таким образом, учителю и учащимся для выполнения указанного номера необходимо обратиться к дополнительным информационным источникам.
Задачи с параметрами с каждым годом пополняются новыми с новым содержанием. На отработку таких задач требуется достаточно много времени (5 часов по программе), умение владеть методами решения различных по условию этих задач.
Для того чтобы успешно сдать экзамен по математике, важно пройти всю программу целиком, а не только «то, что пригодится на экзамене», повысить свою культуру вычислений, то есть минимизировать использование калькуляторов, развивать умение читать графики, правильно использовать терминологию и учить формулы.
Продемонстрирую, как уроках закрепления понятия геометрического смысла производной и некоторых свойств функции в 10 классе я применяю различные приёмы и техники при решении задач.
Математический диктант:
1. Верно ли, что производная от постоянной равна 1.
2. Может ли производная функции f(x) = 14 + 2x принимать отрицательные значения?
3. Завершите предложение, чтобы получилось истинное высказывание: «Значение производной функции в точке ….
Ответы:
1. Показывает ускорение изменения функции;
2. Всегда равно 0;
3. Показывает скорость изменения функции.
4. Верно ли утверждение:
«Если в точке x0 производная функции равна 0, то точка x0 является точкой экстремума».
5. Равно ли нулю значение производной функции f(x) = –3x в точке x0 = –1.
6. Завершите предложение так, чтобы получилось истинное высказывание.
«Если при прохождении … черезточку x0, производная функции меняет свой знак с «-» на «+», то…».
Ответы:
1. Значение производной в точке x0 равно 0.
2. Точка x0 является точкой максимума.
3. Точка x0 является точкой минимума.
7. Расположи в правильной последовательности слова, чтобы получить верное высказывание: Если функция монотонно возрастает на интервале и ее производная монотонно убывает, то функция на этом интервале дифференцируема, а если производная отрицательна, то функция положительна на интервале. (Приём «Верные и неверные утверждения», приём Задания «на дополнение информации», приём Задания «на восстановление текста», приём взаимопроверки).
Задача 1.10. (Актуализация знаний). Написать уравнение прямой, проходящей через указанные точки А и В (Рис. 1):
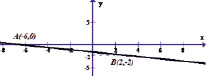
Рис. 1
(Метод применения ИКТ – выполнение самостоятельных заданий; использование компьютера для построения графиков (программа «Graph»)).
Задача 2.10. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0 (Рис. 2). Найти значение производной функции в точке x0.
Решить задачу двумя способами: 1 вариант – геометрически, 2 вариант – аналитически. К доске приглашаются учащиеся из 1 варианта и 2 варианта, задачи решаются на задней стороне доски для дальнейшей проверки ответов.
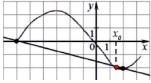
Рис. 2
(Приём обработки графической и текстовой информации, приём «Тонких» и «Толстых» вопросов, технология группового обучения).
Задача 3.10. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0.
а) «Толстый» вопрос: Чем отличаются условия задач 3.10 от 2.10?
б) Найти значение производной функции в точке x0. (Рис. 3)
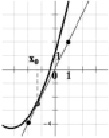
Рис. 3
(Приём обработки графической и текстовой информации: «смыслового чтения и работа с текстом», несплошного текста, таких заданий очень много как в базовом, так в профильном уровне ЕГЭ).
Предложить учащимся решить пункт б) этой задачи 2 способами (1 вариант – аналитически, 2 вариант – геометрически). Ответы сверить и обменяться решениями. (Приём взаимопроверки и взаимообучения).
Задача 4.10. Сравнить полученные значения производных в Задачах 2.10 и 3.10 и связать знак производной (значение углового коэффициента уравнения прямой) с монотонностью функции в окрестности точки x0. Работа в парах. Ответ с места. (Приём обработки графической и текстовой информации: «смыслового чтения и работа с текстом», несплошного и сплошного текста).
Задачи 5.10 и 6.10 выбираются учащимися (дифференцированная работа) и решаются самостоятельно. К доске приглашается двое учащихся и решают Задачу 6.10 на задних сторонах доски с дальнейшей взаимопроверкой.
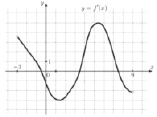
Задача 5.10. На рисунке (Рис. 4) изображен график производной дифференцируемой функции y = f(x). Найдите количество точек графика функции, принадлежащих отрезку [-7;7], в которых касательная к графику функции параллельна прямой, заданной уравнением y = –3x.
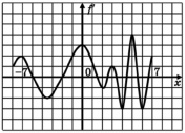
Рис. 4
Задача 6.10. В точке А графика функции y = x3 + 4x + 1 проведена касательная к нему, параллельная прямой y = 4x + 3. Найдите сумму координат точки А. (Технология группового обучения, приём взаимопроверки, приём обработки графической и текстовой информации: «смыслового чтения и работа с текстом», несплошного и сплошного текста, приём «Вопросы к тексту»:
- Прочитайте текст.
- Какие слова встречаются в тексте наиболее часто? Сколько раз?
- Какие слова выделены жирным шрифтом? Почему?
- Если бы вы читали текст вслух, то, как бы вы дали понять, на что обратить внимание?
Речь идет о выделении фразы голосом. Здесь скрывается ненавязчивое, но надежное заучивание. Этот приём используется на этапе формирования новых знаний, первичного закрепления).
Задача 7.10. На рисунке (Рис. 5) изображены график функции и касательные, проведенные к нему в точках с абсциссами A, B, C, D.
а) Пользуясь графиком, установить соответствие между каждой точкой и значением производной функции в ней.
б) Проанализировать решение задачи, составить опорную схему решения задачи (в парах).
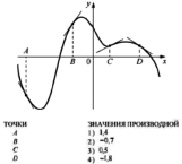
Рис. 5
К доске приглашается учащийся, он решает Задачу 7.10, комментируя решение. Остальные учащиеся становятся оппонентами – 1 вариант, ассистентами – 2 вариант. (Метод применения ИКТ, технология развития критического мышления, приём опорные схемы, приём «Фишбоун», приём взаимопроверки и взаимообучения, методический приём «комментируемое управление», приёмы обработки графической и текстовой информации, приём задания «на соотнесение).
Опорная схема решения задачи (Рис. 6):
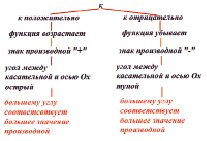
Рис. 6
«Фишбоун» (Рис. 7):
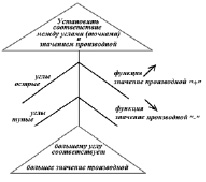
Рис. 7
Часто дети допускают ошибки, не обращая внимания на указанный в задаче промежуток, на котором задается условие задачи, тогда как функция определена на другом промежутке.
1 вариант решает Задачу 8.10., 2 вариант решает Задачу 9.10. После этого обменивайтесь решениями, проверяете друг друга.
Прочитайте текст Задачи 8.10. и Задачи 9.10.
- Какие слова встречаются в тексте наиболее часто? Сколько раз?
- Какие слова выделены жирным шрифтом? Почему?
Если бы вы читали текст вслух, то, как бы вы дали понять, на что обратить внимание?
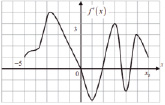
Задача 8.10. На рисунке (Рис. 8) изображён график y = f/(x) производной функции y = f(x), определенной на интервале (-8;4). В какой точке отрезка [-7;-3] функция f(x) принимает наименьшее значение?
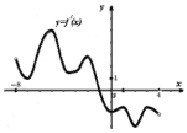
Рис. 8
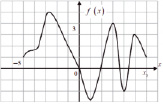
Задача 9.10. На рисунке (Рис. 9) изображён график y = f/(x) производной функции y = f(x), определенной на интервале (-6;5). Найдите точку экстремума функции f(x), принадлежащую отрезку [-5;4].
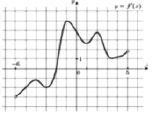
Рис. 9
(Технология группового обучения (работа в парах), приём взаимопроверки, приём обработки графической и текстовой информации: «смыслового чтения и работа с текстом», несплошного и сплошного текста, приём «Вопросы к тексту»).
Дополнительное творческое задание: построить график производной такой функции, у которой имелось бы на указанном промежутке существования функции три экстремума:
1 вариант – точка минимума и две точки максимума, 2 вариант – точка максимума и две точки минимума. (Метод создания заданий творческого характера).
Как было отмечено ранее неправильное чтение графиков и непонимание условия задания – типичные ошибки на экзамене.
Самостоятельная работа.
Задача 10.10. Учащиеся анализируют условие задач, самостоятельно приступают к решению по вариантам с дальнейшей взаимопроверкой.
|
1 вариант |
2 вариант |
|
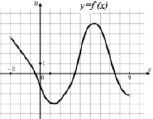
На рисунке изображён график производной функции y = f(x), определённой на промежутке [-5;6]. Найдите количество точек графика f(x), в каждой из которых касательная, проведённая к графику функции, совпадает или параллельна оси абсцисс. |
На рисунке изображён график функции y = f(x), определённой на промежутке [-5; 6]. Найдите количество точек графика f(x), в каждой из которых касательная, проведённая к графику функции, совпадает или параллельна оси абсцисс. |
|
|
|
Задача 11.10.
|
2 вариант |
1 вариант |
|
На рисунке изображен график производной функции y = f/(x), определенной на интервале (-3;9). Найдите промежутки возрастания функции. В ответе укажите сумму |
На рисунке изображен график функции y = f(x), определенной на интервале (-3;9). Найдите промежутки возрастания функции. В ответе укажите сумму |
|
|
|
(Приёмы обработки графической и текстовой информации).
Подготовка к ЕГЭ начинается с урока повторения в 11 классе. Покажу, как на этом уроке я учу детей новым способам решения заданий на тему «Производная функции. Некоторые ее свойства» и подвожу их к решению заданий с параметрами определенного класса.
Задача 1.11. Перечислить все, что вам известно про касательную, проведенную к графику функции y = f(x) в точке x0. (Работа в группе, представление информации на листах А4). (Прием «Корзина» идей, понятий, имен…)
Учащиеся получили на данный урок Д/З: (Прием «заготовки» Д/З на уроки метод дифференцированного обучения)
Решить задачу 1) и на выбор одну из зада 2)-7).
1. Решить уравнение x2 – 3x + 2 = x – 2 тремя способами (2 балла)
2. Построить график функции 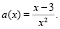 (2 балла)
(2 балла)
3. Построить график функции 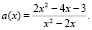 (2 балла)
(2 балла)
4. Построить график функции 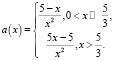 (2 балла)
(2 балла)
5. Построить график функции 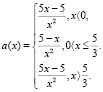 (3 балла)
(3 балла)
(Прием опережающего обучения, прием «заготовки» Д/З на урок)
6. Найти все значения параметра а, при каждом из которых уравнение 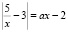 на промежутке (0; +?) имеет 1 корень.
на промежутке (0; +?) имеет 1 корень.
7. (экзамен ЕГЭ 2012) Найти все значения параметра а, при каждом из которых уравнение 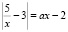 на промежутке (0; +?) имеет более двух корней.
на промежутке (0; +?) имеет более двух корней.
(Метод мозгового штурма, технология групповой работы).
Проверка домашнего задания. 1) x2 – 3x + 2 = x – 2.
1 способ – решают квадратное уравнение или с помощью формулы сокращенного уравнения или с помощью дискриминанта.
2 способ – графический.
(Метод применения ИКТ выполнение домашних заданий; использование компьютера для построения графиков (программа «Graph» Рис. 10), что позволяет учащимся проверить правильность решения, а также во многих ситуациях прогнозировать результат).
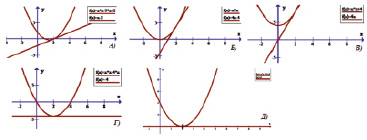
Рис. 10
Итак, решая уравнения графическим способом, получили пять вариантов решения уравнения.
«Толстый» вопрос: Установите закономерность в полученных графиках.
«Тонкий вопрос»: Какова зависимость между решаемыми уравнениями и полученными графиками? (Прямая, входящая в формулу уравнения как правая или левая его часть, – касательная к параболе, задаваемой уравнением).
«Тонкий» вопрос: Можем ли мы решить каждое уравнение, используя свойства касательной, проведенной к параболе? Значит, напрашивается еще один способ решения заданного уравнения.
«Толстый» вопрос: Какое свойство из «Корзины» идей, понятий, имен…» применим?
(Составление опорной схемы).
Решим домашнее задание 1) используя геометрический смысл производной.
1. Значение производной в точке касания есть угловой коэффициент касательной, значение производной в точке касания равен 1, (Определить угловой коэффициент прямой-касательной).
2. Производная функции равна y' = 2x – 3. (Найти производную функции).
3. Составим уравнение y' = k, 1 = 2x – 3, откуда получаем ответ: x = 2. (Геометрический смысл производной в точке: k = f/(x0), где x0 – точка касания. Приравнять угловой коэффициент прямой к производной функции и, решив полученное уравнение, записать ответ). Ответ: x = 2. (Методический приём «комментируемое управление», приём «Вопросы к тексту», прием «Тонких» и «Толстых» вопросов).
Решим задачу. К доске приглашается учащийся по желанию. Отработаем выработанный алгоритм решения задачи.
«Тонкий» вопрос: Согласны ли вы, что к данной задаче можно применить выработанный алгоритм?
«Тонкий» вопрос: Достаточно ли данных в задаче для её решения? Уточните, каких данных не хватает?
«Тонкий» вопрос: Что нужно найти?
«Тонкий» вопрос: Каким свойством прямых необходимо воспользоваться, чтобы определить угловой коэффициент прямой-касательной?
Задача 1.11. Прямая y = 4x + 8 параллельна касательной к графику функции y = x2 – 5x + 7. Найдите абсциссу точки касания.
Решение.
Так как касательная параллельна прямой y = 4x + 8, их угловые коэффициенты равны k = 4. Производная функции y' = 2x – 5. Составим уравнение y' = k, 4 = 2x – 5. Геометрический смысл производной в точке: k = f/(x0), где x0 – точка касания. Решим уравнение: 2x0 – 5 = 4, откуда x0 = 4,5. Ответ: 4,5.
(Технология групповой работы, методика «Взаимообмен заданиями», приём обработки графической и текстовой информации, приём «смыслового чтения и работа с текстом», технология развития критического мышления, приём «Тонких» и «Толстых» вопросов).
Задача 2.11.1. Прямая y = –3x – 8 является касательной к графику функции f(x) = ax2 + 27x + 7. Найдите значение параметра а.
Задача 2.11.2. Прямая y = –3x – 8 является касательной к графику функции f(x) = x2 + bx + 7. Найдите значение параметра а.
«Вызов»: «Тонкий» вопрос: Достаточно ли данных в задаче для её решения? (восприятие текста, поиск информации и понимание прочитанного).
«Толстый» вопрос: Можно ли применить выработанный алгоритм?
«Толстый» вопрос: С какой проблемой столкнулись? (извлечение смысла, преобразование и интерпретация текста).
«Осмысление»: «Толстый» вопрос: Что нужно сделать, чтобы решить эту проблему? (Обратиться в «Корзины» идей, понятий, имен…» или найти другой выход), (оценка полученной информации, сопоставление с условием).
«Рефлексия»: Задача 2.11.1 и Задача 2.11.2.
Задача 2.11.1. Прямая y = –3x – 8 является касательной к графику функции f(x) = ax2 + 27x + 7. Найдите значение параметра а.
Решение. Воспользуемся условием касания графика функции y = f(x) и прямой y = –3x – 8:
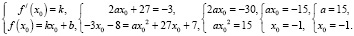
Ответ: а = 15.
Задача 2.11.2. Прямая y = –3x – 8 является касательной к графику функции f(x) = x2 + bx + 7. Найдите значение параметра а.
Решение. Воспользуемся условием касания графика функции y = f(x) и прямой y = –3x – 8:
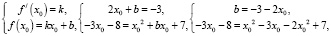
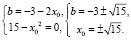
Ответ: 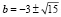 .
.
Итак, какими способами мы пользовались, решая уравнения? (Аналитически, используя геометрический смысл производной, уравнение касательной-прямой с угловым коэффициентом и графически).
Эффективным приёмом является работа в группах над творческим заданием. Его можно применять в основной части занятия. Работа в группе формирует умения слышать друг друга, высказывать собственное мнение, находить компромиссы, работать в команде и проявить лидерские качества. Все эти умения очень важны не только для профессиональной деятельности, но и для любой жизненной ситуации. А для подростков умения выстроить коммуникацию особенно важно.
Выработайте хотя бы три решения следующей задачи. (Прием мозгового штурма, технология групповой, приём презентации полученных результатов на уроке путём сканирования материала, решения).
Задача 3.11. При каких значениях параметра a уравнение 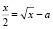 имеет единственное решение? (Работа в группе 4 учащихся).
имеет единственное решение? (Работа в группе 4 учащихся).
Решение 1. Если прямая 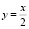 касается графика функции
касается графика функции 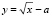 в точке с абсциссой x, тополучаем систему уравнений:
в точке с абсциссой x, тополучаем систему уравнений:
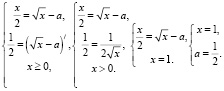
Ответ: 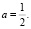
Решение 2. Если прямая 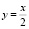 касается графика функции
касается графика функции 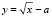 в точке с абсциссой x, то получаем систему уравнений:
в точке с абсциссой x, то получаем систему уравнений:
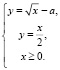
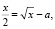

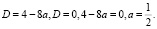
Ответ: 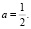
Решение 3. Общий вид уравнения касательной y = f(x0) + f/(x0)•(x – x0) = f/(x0)•x + (f(x0) – f/(x0)•x0), уравнение прямой y = kx + b,
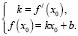
Касательная к графику функции 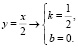
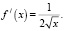
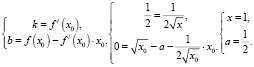
Ответ: 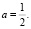
(Прием мозгового штурма, технология групповой работы,прием презентации полученных результатов на уроке путем сканирования материала, решения, приём «Фантастическая добавка»).
Задача 4.11. (Еженедельная учебно-методическая газета «Математика», издательский дом «Первое сентября», № 16, 2004) При каких значениях параметра а уравнение ax2 –x + 3 = 0 имеет единственное решение?
Решение.
1 способ. Аналитический способ. Рассмотрим два случая:
1. a = 0. При этом значении параметра а уравнение принимает вид –x + 3 = 0, откуда x = 3. Это единственное решение.
2. a ≠ 0. Тогда ax2 –x + 3 = 0 – квадратное уравнение, дискриминант которого
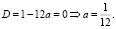
Ответ: 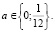
2 способ.
1. a = 0. При этом значении параметра а уравнение принимает вид –x + 3 = 0, откуда x = 3. Это единственное решение.
2. ax2 = x – 3.
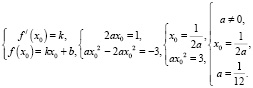
Ответ: 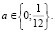
(Приём «Вопросы к тексту»). Какой способ (метод) решения задач с параметром применяли?
Способ I (аналитический). Это способ так называемого прямого решения, повторяющего стандартные процедуры нахождения ответа в задачах без параметра.
Комментарий. Аналитический способ решения задач с параметром есть самый трудный способ, требующий высокой грамотности и наибольших усилий по овладению им.
Найдите в тексте следующего предложения, описывающего графический способ решения уравнений с параметром необычное в учебной ситуации.
Способ II (графический). В зависимости от задачи (с переменной х и параметром а) рассматриваются графики или в координатной плоскости (х; у), или в координатной плоскости (х; а).
(Прием заготовки Д/З на урок).
Решим Задачу 4.113 способом. Выполняя Д/З, построили график функции (Рис. 11) 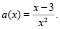
Путем тождественных преобразований выразим из уравнения функцию 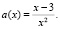
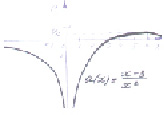
Рис. 11
(Приём «Кластер» (Рис. 13), приём «Тонких» и «Толстых» вопросов, технология группового обучения, приёмы обработки графической и текстовой информации, метод создания заданий творческого характера, задачи на поиск закономерностей).
«Толстый вопрос»: Что объединяет уравнения, решенные на уроке? Какое условие накладывается на уравнение? Решите задачу в паре, применяя любой известный вам способом и составьте «кластер» решения уравнения.
Задача 5.11. (Еженедельная учебно-методическая газета «Математика», издательский дом «Первое сентября», № 16, 2004). При каких значениях параметра а уравнение 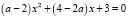 имеет единственное решение?
имеет единственное решение?
Решение. 1 способ. Аналитический.
1. При a = 2 исходное уравнение решений не имеет.
2. При a ≠ 2 уравнение является квадратным и примет вид: 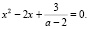 Искомые значения параметра – корни дискриминанта, который обращается в нуль: a = 5.
Искомые значения параметра – корни дискриминанта, который обращается в нуль: a = 5.
Ответ: a = 5.
2 способ. Аналитический.
При a = 2 исходное уравнение решений не имеет.
(a – 2)x2 = (2a – 4)x – 3.
Используем геометрический смысл производной: значение производной в точке касания есть угловой коэффициент касательной. 2a – 4 = (2a – 4)x, откуда подставим найденное значение x = 1 в исходное уравнение и получим, что a = 5. Ответ: a = 5.
(Прием заготовки Д/З на урок). 3 способ. Путем тождественных преобразований выразим функцию 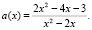

Рис. 12
Метод обучения на опережение, метод «Д/З по задачам ЕГЭ с дальнейшей презентацией решений» позволяет учащимся детально разобраться с задачей, при необходимости воспользоваться Интернет-ресурсами, столкнуться с проблемой и перейти к решению этой проблемы альтернативным путем.
(Метод проектов, прием «Д/З по задачам ЕГЭ с дальнейшей презентацией решений», прием опережающего обучения, прием презентации полученных результатов на уроке путем сканирования материала, решения, метод создания заданий творческого характера).
Решим домашнюю задачу 6), выбрать наиболее рациональный вариант решения. Внести такие изменения в уравнение или в условие задачи, чтобы применение выработанного алгоритма было невозможным. Найти все значения параметра а, при каждом из которых уравнение 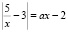 на промежутке (0; +∞) имеет 1 корень.
на промежутке (0; +∞) имеет 1 корень.
Решение. 1 способ.
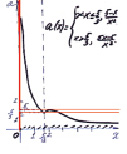
Рис. 14
Ответ: Один корень при 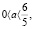
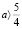 .
.
2 способ. 1 кусок функции
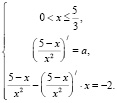
2 кусок функции
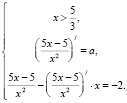
Как видим, появляется совокупность двух систем, решение которых станет трудо- и времяемким.
(Технология группового обучения, метод проектов, прием «Д/З по задачам ЕГЭ с дальнейшей презентацией решений», прием опережающего обучения, прием презентации полученных результатов на уроке путем сканирования материала, решения, приём «Вопросы к тексту», технология развития критического мышления).
Задание группе. Прочитайте текст домашней задачи 7).
Какие слова выделены жирным шрифтом? Почему?
Если бы вы читали текст вслух, то, как бы вы дали понять, что это словосочетание главное?
Появляется проблемная ситуация. Какая (какие)?
Можем ли использовать выработанные алгоритмы?
Какой видите выход?
Знаете ли вы способ решения этой задачи?
Решите задачу, оформив ее решение на листе А4.
Задача7).(экзамен ЕГЭ 2012) Найти все значения параметра а, при каждом из которых уравнение 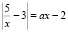 на промежутке (0; +∞) имеет более двух корней.
на промежутке (0; +∞) имеет более двух корней.
Решение.
1 способ. Рассмотрим функции 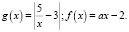 Исследуем уравнение g(x) = f(x) на промежутке (0; +∞).
Исследуем уравнение g(x) = f(x) на промежутке (0; +∞).
При a ≤ 0 все значения функции f(x) на промежутке (0; +∞) отрицательны, а все значения второй функции неотрицательны, поэтому уравнение g(x) = f(x) на промежутке (0; +∞)не имеет решений при a ≤ 0.
При 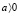 функция f(x) возрастает. Функция g(x) убывает на промежутке
функция f(x) возрастает. Функция g(x) убывает на промежутке 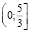 , поэтому уравнение g(x) = f(x) имеет не более одного решения на промежутке
, поэтому уравнение g(x) = f(x) имеет не более одного решения на промежутке 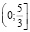 , причем решение будет существовать тогда и только тогда когда
, причем решение будет существовать тогда и только тогда когда 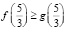 , откуда получаем
, откуда получаем 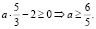
На промежутке 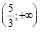 уравнение g(x) = f(x) примет вид
уравнение g(x) = f(x) примет вид 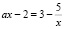 , которое сводится к квадратному уравнению: ax2 – 5x + 5 = 0. Будем считать, что
, которое сводится к квадратному уравнению: ax2 – 5x + 5 = 0. Будем считать, что 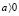 , так как случай a ≤ 0 был рассмотрен ранее. Дискриминант этого уравнения
, так как случай a ≤ 0 был рассмотрен ранее. Дискриминант этого уравнения 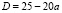 , поэтому при
, поэтому при 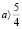 уравнение не имеет корней, при
уравнение не имеет корней, при 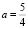 имеет единственный корень x = 2, при
имеет единственный корень x = 2, при 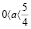 имеет два решения.
имеет два решения.
Если уравнение имеет два корня x1, x2, то при 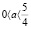 , больший корень
, больший корень 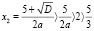 ,
,
поэтому он принадлежит промежутку 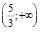 . Меньший корень x1 принадлежит промежутку
. Меньший корень x1 принадлежит промежутку 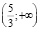 тогда и только тогда, когда
тогда и только тогда, когда 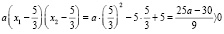 , то есть
, то есть 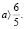
Таким образом, уравнение 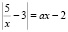 на промежутке (0; +∞) имеет следующее число корней:
на промежутке (0; +∞) имеет следующее число корней:
1. Нет корней при a ≤ 0; 2. Один корень при 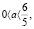
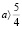 ; 3. Два корня
; 3. Два корня 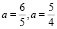 ; 4. Три корня
; 4. Три корня 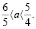
Ответ: 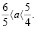
2 способ. Комментарий: Ограниченность времени мастер–класса не позволяет раскрыть технологию проектирования, которая является основной технологией работы с учащимися. В этой связи участникам мастер–класса наглядно демонстрируются основные результаты, а именно реализованный проект.
Путем тождественных преобразований выразим функцию 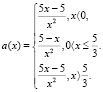
Строим график функции (рис. 15), который приводит к полученному ответу.
Ответ: 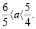
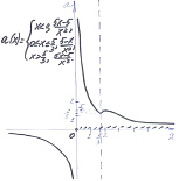
Рис. 15
Итак, сегодня мы с вами повторили свойства функции. Какие именно?
(Методический приём «комментируемое управление» с составлением опорный схемы).
Д/З: 1) Найдите всевозможные значения параметра а, при каждом из которых уравнение 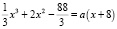 имеет ровно одно решение.
имеет ровно одно решение.
2) № 18, Вариант 12, 23, 26 Типовые экзаменационные варианты ЕГЭ 2018, профильный уровень, под ред. И.В. Ященко.
Самостоятельная работа по разработке собственной модели занятия в режиме продемонстрированной технологии.
С/Р: Задача 7.11. 1. Найдите все значения параметра a, при каждом из которых графики функций f(x) = x2 + 2x – 3 и ay + 5x + 6a = 0 имеют ровно одну точку пересечения.
А. Дистервег: «Если человека постоянно приучать усваивать знания и умения в готовом виде, можно и притупить его природные творческие способности – «разучить» думать самостоятельно». Современный урок математики – урок, на котором дети сами добывают знания, а учитель умело в этом им помогает.
Библиографическая ссылка
Рылова И.Г. ИЗ ОПЫТА ПОДГОТОВКИ УЧАЩИХСЯ К ЕГЭ ПО МАТЕМАТИКЕ // Международный школьный научный вестник. 2018. № 6-1. ;URL: https://school-herald.ru/ru/article/view?id=814 (дата обращения: 03.03.2026).