Роль математики в различных областях естествознания очень велика. В школе на уроках алгебры мы изучали интересную тему «Производная». Меня заинтересовало применение производной в физике и химии, так как я планирую поступать в технических вуз. В школьном курсе математике рассказывается лишь о малом применении производной.
Понятие производной занимает уникальное положение в школьной программе. С одной стороны, производная активно используется: с её помощью исследуются функции и строятся графики, ищутся наибольшие и наименьшие значения функций; школьникам надо уметь решать задачи на геометрический и физический смысл производной. С другой стороны, не дается строгое определение определения. Вследствие чего учащимся приходится заучивать таблицу производных и правила дифференцирования. При этом многие умеют лишь механически выполнять некоторые действия и решать типовые задачи, не понимая сути того, что они делают. В свою очередь производная в дальнейшем изучается в вузе на занятиях по высшей математике, применяется в физике и химии.
Производная – фундаментальное математическое понятие, используемое в различных вариациях во многих разделах математики. Это базовая конструкция дифференциального исчисления, допускающая много вариантов обобщений, применяемых в математическом анализе, алгебре, физике и химии.
Дифференциальное исчисление – это описание окружающего нас мира, выполненное на математическом языке. Производная помогает нам успешно решать не только математические задачи, но и задачи практического характера в разных областях науки.
Производная функции используется всюду, где есть неравномерное протекание процесса: это и неравномерное механическое движение, и переменный ток, и химические реакции и радиоактивный распад вещества и т.д.
Цель исследования: выявить применение производной в физике и химии.
Объект исследования – производная и ее применение.
Предмет исследования – применение производной в физике и химии.
Гипотеза: «Применение производной значительно облегчает решение задач в физике и химии».
Исходя из цели и предмета исследования, для доказательства гипотезы были поставлены следующие задачи:
1. Провести анализ литературы о производной и ее применении.
2. Выявить применение производной в физике.
3. Показать применение производной при решении физических и химических задач.
Для достижения цели и решения поставленных задач применен комплекс методов исследования:
– теоретические: изучение и анализ литературы и научно-исследовательских работ по теме исследования;
– эмпирические: наблюдение, опрос, анкетирование, проведение опытно-экспериментальной работы.
Производная и ее применение
На уроках алгебры в 10 классемы познакомились с определением производной, как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует.
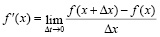 .
.
Действие нахождения производной функции называется её дифференцированием, а функцию, имеющую производную в точке х, называют дифференцируемой в этой точке. Функция, дифференцируемая в каждой точке промежутка, называется дифференцируемой в этом промежутке.
Большая часть открытия основных законов математического анализа принадлежат английскому физику и математику Исааку Ньютону и немецкому математику, физику, философу Лейбницу.
Ньютон ввел понятие производной, изучая законы механики, тем самым раскрыл её механический смысл.
Физический смысл производной: производная функции y=f(x) в точке x0 – это скорость изменения функции f(x) в точке x0 (рис. 1).
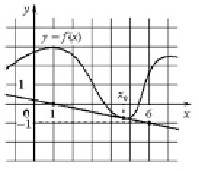
Рис. 1
Лейбниц пришёл к понятию производной, решая задачу проведения касательной к производной линии, объяснив тем самым ее геометрический смысл.
Геометрический смысл производной состоит в том, что производная функция в точке x0 равна угловому коэффициенту касательной к графику функции, проведенной в точке с абсциссой x0 (рис. 2).
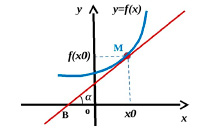
Рис. 2
Термин «производная» и современные обозначения y=f(x) ввёл Ж. Лагранж в 1797 г.
Применение производной в физике
Исторически понятие производной возникло из практики. Скорость неравномерного движения, плотность неоднородной материальной линии, а также тангенс угла наклона касательной к кривой и другие величины явились прообразом понятия производной. Возникнув из практики, понятие производной получило обобщаемый, абстрактный смысл, что ещё более усилило его прикладное значение. Создание дифференциального исчисления чрезвычайно расширило возможности применения математических методов в естествознании и технике. В таблице представлены формулы нахождения одной физической величины через производную другую.
Производная в физике
|
υ(t) = х′(t) |
скорость |
|
a (t)=υ′ (t) |
ускорение |
|
J(t) = q′(t) |
сила тока |
|
C(t) = Q′(t) |
теплоемкость |
|
d(l)=m′(l) |
линейная плотность |
|
K(t) = l′(t) |
коэффициент линейного расширения |
|
ω (t)= φ′(t) |
угловая скорость |
|
а(t)= ω′(t) |
угловое ускорение |
|
N(t) = A′(t) |
мощность |
Производная в электротехнике
В наших домах, на транспорте, на заводах всюду работает электрический ток. Под электрическим током понимают направленное движение свободных электрически заряженных частиц.
Количественной характеристикой электрического тока является сила тока.
В цепи электрического тока электрический заряд меняется с течением времени по закону q=q (t). Сила тока I есть производная заряда q по времени.
В электротехнике в основном используется работа переменного тока.
Электрический ток, изменяющийся со временем, называют переменным. Цепь переменного тока может содержать различные элементы: нагревательные приборы, катушки, конденсаторы.
Получение переменного электрического тока основано на законе электромагнитной индукции, формулировка которого содержит производную магнитного потока.
Производная в химии
И в химии нашло широкое применение дифференциальное исчисление для построения математических моделей химических реакций и последующего описания их свойств.
Производную в химии используют для определения очень важной вещи – скорости химической реакции, одного из решающих факторов, который нужно учитывать во многих областях научно-производственной деятельности.
Заключение
Таким образом, не зная, что такое производная, нельзя понять, что такое первообразная и интегрирование. А без него нельзя будет решать дифференциальные уравнения в высшей математике, химии и физики. По результатам проведенного исследования можно сделать вывод о том, что применение производной функции весьма многообразно и не только при изучении математики, но и других дисциплин.
Библиографическая ссылка
Скрипченко И.М. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ В ФИЗИКЕ И ХИМИИ // Международный школьный научный вестник. 2018. № 6-2. ;URL: https://school-herald.ru/ru/article/view?id=840 (дата обращения: 29.01.2026).
