В одной из книг венгерского математика Ласло Фейеш Тот[1] «Расположение на плоскости, на сфере и в пространстве» [6] я увидела такую изопериметрическую задачу: «Какое из выпуклых тел, имеющих равные по величине поверхности, имеют наибольший объем?» Меня данная задача заинтересовала, и я решила проверить этот факт на стереометрических фигурах, изучаемых в школьной программе.
Начав создание этой работы, я опиралась на исследование изопериметрического неравенства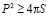 
, которое нашла в одной из литератур. Так как я учусь в одиннадцатом классе, мне бы хотелось получить неравенство для стереометрических фигур. Такого неравенства в школьной программе не нашла, поэтому мне захотелось составить его самой. В итоге я получила 
.
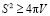В процессе доказывания неравенства появилась проблема, которая заключалась в следующем: я не учла, что у S единицы измерения в квадрате, который при возведении во вторую степень площади превращается в четвертую степень, а единицы объема измеряются в третьей степени, т.е. в кубе.
Следовательно, мне нужно было согласовывать единицы измерения и увеличить коэффициент. В итоге, уже после моего выведения, в одной литературе я нашла изопиранное[2] неравенство: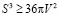 
, где S – площадь, V – объем, а π – известное иррациональное число, определяемое как отношение длины окружности к его диаметру.
Цель исследования: выяснить истинно или ложно изопиранное неравенство в трехмерном пространстве.
В соответствии с поставленной целью были определены задачи:
Определение объектов исследования (выписать из школьного курса геометрии объемные тела, соответствующие определению стереометрической фигуры, расположить их от простых к более сложным).
Изучение форм площадей и объемов объектов исследования, способов доказательства неравенств.
Доказать неравенства для каждой из рассматриваемых фигур, затем перейти к доказательству в общем виде.
Гипотеза: изопиранное неравенство верно для трехмерного пространства.
В качестве методов исследования применялись: работа с источниками информации, а также практическая работа на доказательства неравенств на конкретных примерах.
Объект исследования – изопиранное неравенство.
Предмет исследования – процесс доказательства неравенств.
Теоретическая и практическая значимость результатов данной работы – это применение данного материала на уроках математики, на внеурочной деятельности и использование приводимого мною неравенства для практического применения. Основными компонентами работы являются доступность, практическая направленность изучаемого материала.
1. Теоретические сведения о геометрических фигурах в пространстве
1.1. Многогранники
Для лучшего понимания напомним некоторые сведения о многогранниках и дадим каждому многограннику наглядное описание.
Куб представляет собой многогранник, у которого шесть граней, и все они – равные квадраты. У куба 12 равных ребер и 8 вершин (см. приложение 1).
;
.
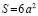Параллелепипед представляет собой многогранник, у которого шесть граней, и каждая из них – параллелограмм. Параллелепипед может быть прямым (см. приложение) или наклонным (см. приложение 2).
;
.
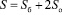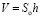Пирамида представляет собой многогранник, одна грань которого, называемая основанием пирамиды, – некоторый выпуклый n-угольник, а остальные n граней – треугольники с общей вершиной (см. приложение 3). Эта общая вершина называется вершиной пирамиды, а треугольники – боковыми гранями пирамиды.
;
.
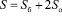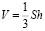Призма представляет собой многогранник, две грани которого, называемые основаниями призмы, – равные n-угольники, а все остальные n граней – параллелограммы. Они называются боковыми гранями призмы. Призма может быть прямой (см. приложение 4) или наклонной (см. приложение 5). У прямой призмы все боковые грани – прямоугольники, у наклонной призмы хотя бы одна грань – параллелограмм, не являющийся прямоугольником.
;
.
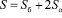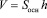1.2. Тела вращения
Цилиндр – геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её (см. приложение 6).
.
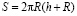
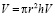Конус – тело в евклидовом пространстве, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность. Иногда конусом называют часть такого тела, имеющую ограниченный объём и полученную объединением всех отрезков, соединяющих вершину и точки плоской поверхности (последнюю в таком случае называют основанием конуса, а конус называют опирающимся на данное основание) (см. приложение 7).
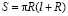
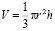
Шаром называется множество всех точек пространства, расстояние от каждой из которых до данной точки – центра шара – не превосходит данного положительного числа, которое называется радиусом шара (см. приложение 8).
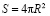
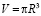
Сферой называется множество всех точек пространства, удаленных от данной точки, называемой центром сферы, на одно и то же расстояние (см. приложение). Отрезок, соединяющий любую точку сферы с ее центром, называется радиусом сферы. Радиусом сферы называют также расстояние от любой точки сферы до ее центра. Для сферы, как и для окружности, определяются хорды и диаметр (см. приложение 9).
1.3. Неравенство Коши в Евклидовом пространстве[3]
Огюстен Луи Коши (1789–1857) – французский математик, основоположник теории аналитических функций.
Среднее арифметическое двух неотрицательных чисел не меньше их среднего геометрического – это неравенство называется неравенством Коши: если
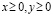, то 
.
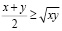Неравенство Коши часто используют при доказательстве других неравенств. А само оно доказывается так:
составим разность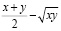 
.
Имеем:
.
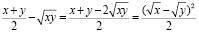Неравенство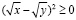 
верно при любых неотрицательных значениях x и y. Значит,
,
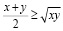причем равенство имеет место лишь в случае x = y.
Из неравенства Коши, в частности, следует неравенство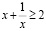 
, справедливое для всех x > 0.
В более общем виде: для неотрицательных чисел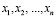 
справедливо неравенство между их средним арифметическим и средним геометрическим
,
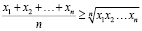причем равенство возможно лишь при условии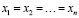 
.
Вывод. Все стереометрические тела, рассматриваемые в школьном курсе геометрии, имеют свои свойства и формулы, с помощью которых можно вычислить площадь поверхности и их объем.
2. Изопиранное неравенство
Рассмотрим доказательство изопиранного неравенства
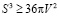
на конкретных фигурах, затем перейдем к доказательству в общем виде.
2.1. Изопиранное неравенство для многогранников
1. Доказательство неравенства для куба
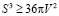
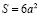
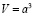
Подставим данные формулы в неравенство, получим:
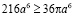
Разделим обе части неравенства на 36a2 получим: (верно)
.
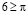2. Доказательство неравенства для прямоугольного параллелепипеда
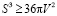
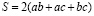
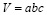
Заменим π на 4 (Если неравенство будет выполняться при 4, то оно будет выполняться и при π):
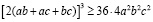
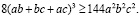
Разделим обе части неравенства на 8, получим:
.
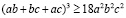Извлечем корень 3 степени:
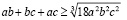(1)
Докажем это неравенство с помощью неравенства Коши (среднее арифметическое не меньше среднего геометрического):
,
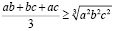умножим на 3:
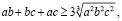
и внесем 3 под корень:
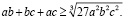(2)
Мне нужно доказать, что
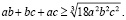
Так как в (1) и (2) неравенствах левые части одинаковые, следовательно, надо доказать, что:
.
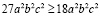Разделим на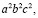 
получим:
27≥18 (верно)
3. Доказательство неравенства для треугольной правильной призмы
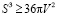
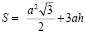
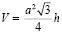
Сразу заменим π на 4:
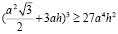
Извлечем корень:
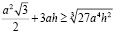(3)
Воспользуемся неравенством Коши, предварительно разбив: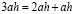 
.
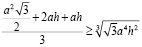Умножим на 3 и сразу внесем тройку под знак корня:
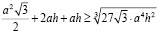(4)
Левые части неравенств (3) и (4) равны, следовательно, можно сравнить правые части этих неравенств:
.
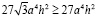Разделим обе части на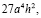 
получим
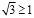(верно).
4. Доказательство неравенства для правильной треугольной пирамиды
.
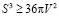
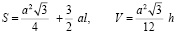Заменим π на 4:
.
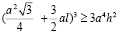Заменим
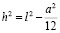
(по теореме Пифагора) и извлечем корень:
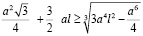. (9)
Воспользуемся неравенством Коши как делали ранее, разбив
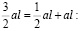
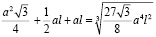(10)
Сравним правые части неравенств (9) и (10):
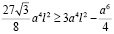
Занесем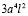 
в левую часть, получим:
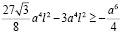
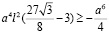
Полученное неравенство верно т.к. в левой части положительное число, а в правой – отрицательное.
Доказательство неравенства для правильной четырехугольной пирамиды
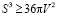
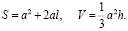
Заменим π на 4:
.
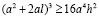Заменим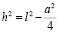 
(теорема Пифагора) и извлечем корень:
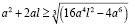(11)
Воспользуемся теоремой Коши, разбив
:
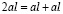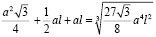
Умножим обе части неравенства на 3 и внесем тройку под знак корня в правой части неравенства:
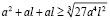(12)
Сравним подкоренные выражения в правых частях полученных неравенств (11) и (12):
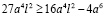
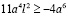(верно)
2.2. Изопиранное неравенство для тел вращения
1. Доказательство неравенства для цилиндра
, 
.
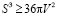
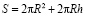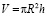Сразу заменим π на 4 в правой части неравенства:
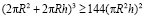
Извлечем корень из каждой части неравенства, получим:
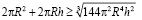(5)
Воспользуемся неравенством Коши, предварительно разбив
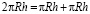
и выполнив манипуляции с тройкой, какие мы делали ранее:
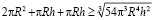(6)
А далее сравним правые части неравенств, как делали ранее:
,
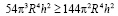разделим обе части на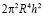 
:
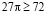, (верно)
2. Доказательство неравенства для конуса
.
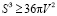
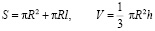Заменим π на 4 в правой части неравенства:
,
.
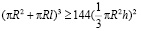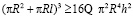Заменим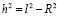 
(по теореме Пифагора), раскроем после подстановки скобки и извлечем корень:
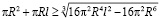(7)
Воспользуемся неравенством Коши как в предыдущих случаях, разбив
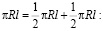
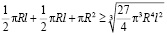(8)
Сравним правые части неравенств (7) и (8):
,
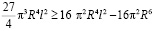перенесем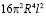 
в левую часть и вынесем 
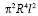за скобки:
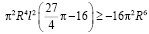
неравенство верно, т.к. в левой его части положительное число, а в правой части – отрицательное.
3. Доказательство неравенства для шара (сферы)
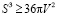
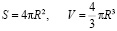
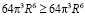(верно).
2.3. Доказательство неравенства в общем виде
Докажем это утверждение методом от противного. Предположим, что найдется хотя бы одна стереометрическая фигура, для которой не выполняется наше неравенство, а выполняется противоположное: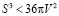 
, отсюда 
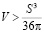, это означает, что объем может принять в качестве наименьшего значения 
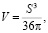а мы знаем, что это есть наибольшее значение площади, соответствующее единственной фигуре – шару.
Действительно, как мы видели, для шара:
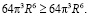
Получили противоречие:
V не может быть больше, чем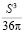 
, значит, 
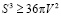всегда.
2.4. Применение изопиранного неравенства к стереометрическим фигурам
Задача 1. Докажите неравенство для прямого параллелепипеда, в основании которого ромб.
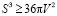
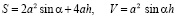
Опять же сразу заменим π на 4:
,
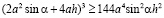извлечем корень:
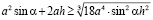
Воспользуемся неравенством Коши, предварительно разбив
:
,
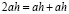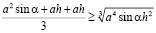умножим на 3, занесем 3 под знак корня и сравним правую часть из неравенства Коши и неравенства, доказуемого мною:
,
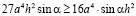разделим на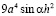 
:
,
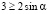т.к. наибольшее возможное значение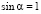 
, получившееся неравенство верно.
Задача 2. Докажите неравенство для прямого параллелепипеда, в основании которого параллелограмм.
,
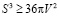
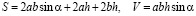Заменим π на 4:
,
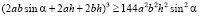Разделим обе части на 8, извлечем корень:
,
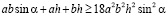Воспользуемся неравенством Коши:
,
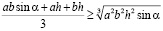опять же умножим на 3, внесем ее под корень, сравним правые части неравенств:
.
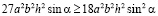Разделим на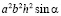 
: 
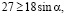т.к. наибольшее возможное значение 
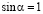, полученное неравенство верно.
Задача 3. Докажите изопиранное неравенство для прямоугольной равнобедренной пирамиды, высота которой совпадает с боковым ребром.
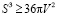
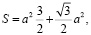
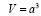, заменим π на 4:
,
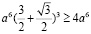сократим на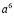 
:
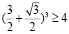(верно).
Задача 4. Докажите изопиранное неравенство для прямоугольной равнобедренной пирамиды, высота которой падает в центр описанной около основания окружности.
,
,
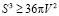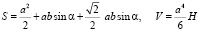заменим π на 4:
,
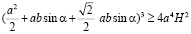Извлечем корень:
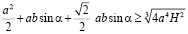
Воспользуемся неравенством Коши, сразу умножив обе части неравенства на 3:
,
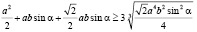т.к. левые части у нас одинаковые, можно сравнить правые:
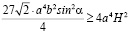
Заменим
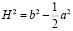
(Прямоугольный треугольник и радиус описанной окружности),
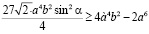
перенесем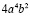 
влево, получим:
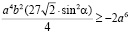(верно).
Задача 5. Докажите изопиранное неравенство для прямоугольной равнобедренной пирамиды, высота которой падает в центр вписанной окружности.
,
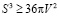
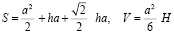сразу заменим π на 4:
.
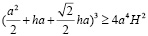Извлечем корень:
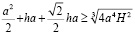
Воспользуемся неравенством Коши:
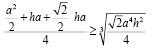
Умножим обе части на 3 и внесем в правой части 3 под корень:
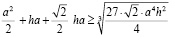
Сравним правые части как делали ранее:
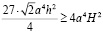
Заменим
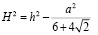
и умножим обе части на 4:
,
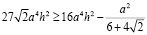
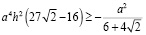(верно, т.к. слева положительное число, а справа – отрицательное).
Вывод: таким образом, изопиранное неравенство верно для всех стереометрических фигур. Суть изопиранного неравенства: если дан ряд стереометрических тел с одинаковой площадью, наибольший объем будет иметь шар. И наоборот: если дан ряд стереометрических тел с одинаковым объемом, наименьшую площадь будет иметь шар (сфера).
Заключение
В процессе исследовательской работы были решены поставленные задачи и получены следующие результаты и выводы:
Доказала справедливость неравенства для стереометрических фигур изучаемых в школьной программе.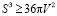 
2. Доказала справедливость данного соотношения в общем виде, а также доказала факт превращения этого неравенства в истинное равенство для сферы или шара.
3. Провела статистическую обработку данных на применение известных теорем для доказательства изопиранного неравенства для стереометрических фигур (см. приложение 10).
В процессе проведенного исследования гипотеза, о том, что изопиранное неравенство верно для трехмерного пространства, подтверждена.
Приложения
Приложение 1
Куб
Приложение 2
Параллелепипед
Приложение 3
Пирамида
Приложение 4
Призма
Приложение 5
Наклонная призма
Приложение 6
Цилиндр
Приложение 7
Конус
Приложение 8
Шар
Приложение 9
Сфера
Приложение 10
Применение известных теорем для доказательства неравенств стереометрических фигур
|
Применение неравенства Коши |
Применение теоремы Пифагора |
Использование метода от противного |
|
10 |
3 |
1 |
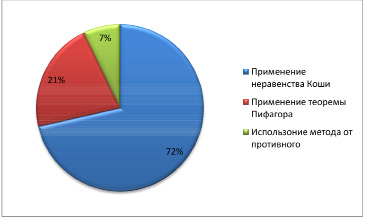
Применение известных теорем для доказательства неравенств стереометрических фигур
[1]Ласло Фейеш Тот (Сегеда, 12 марта 1915 — Будапешт, 17 марта 2005) — венгерский математик. Наряду с Коксетером и Эрдёшем, Фейеш Тот считается родоначальником комбинаторной геометрии.
[2]Изопиранное неравенство – это общий термин для обозначения неравенства между объемом и площадью плоской поверхности.
[3]Евкли́дово простра́нство (также эвкли́дово простра́нство) — в изначальном смысле, пространство, свойства которого описываются аксиомами евклидовой геометрии. В этом случае предполагается, что пространство имеет размерность, равную 3.
Библиографическая ссылка
Степанова Д.А. ИЗОПИРАННОЕ НЕРАВЕНСТВО // Международный школьный научный вестник. – 2019. – № 1-3. ;URL: https://school-herald.ru/ru/article/view?id=898 (дата обращения: 03.01.2025).