Международный школьный научный вестник

Научный журнал для старшеклассников и учителей ISSN 2542-0372

• Авторы
• Научный руководитель
• Файлы
• Литература

Калиманов И.М. 1

---

1 МОУ «Ильинская СОШ №25», 11 класс

Кулешов П.С. (, ЦИАМ)

Кузнецова Т.И. (, МОУ «Ильинская СОШ №25»)

Статья в формате PDF

0 KB

1. Куликов И.Ю. Эффект Магнуса // Чудесности вокруг нас. – М.: Инноватэк, 2017.

2. Бородин И.Д., Берестова Е., Берестова С.А., Войцык А. Эффект Магнуса. – Екатеринбург: ФГАОУ ВПО «УрФУ им, первого Президента России Б.Н. Ельцина».

3. Андреев А., Панов А., Панов П. Эксперименты с эффектом Магнуса // Квант. – 2017. – №2. – С. 41–44.

Об Эффекте Магнуса знают не все, но, скорее всего, каждый хоть раз в жизни с ним сталкивался при просмотре таких видов спорта как футбол, волейбол или теннис. Поводом для открытия и изучения этого эффекта послужило отклонение пушечного ядра от начальной траектории. Эффект был замечен и описан в восемнадцатом веке, и только в середине девятнадцатого века, в 1853 году, немецкий физик Генрих Густав Магнус предложил физическое объяснение искривления траектории полёта пушечного ядра, вследствие его вращения. «К сожалению, никаких количественных измерений, в ходе своих аэродинамических опытов, Магнус не проводил, а лишь зафиксировал возникновение отклоняющей силы и совпадение её направления с тем, которое имело место в артиллерийской практике» [1].

Цель работы: выдать рекомендации по наиболее оптимальному, с точки зрения практики, созданию подъёмной силы на основе Эффекта Магнуса.

Актуальность: можно указать множество примеров проявления Эффекта Магнуса в природе и технике: уклонение вертикальных вихрей в атмосфере от начальных траекторий; подача закрученного мяча в таких спортивных играх, как футбол, волейбол, теннис; создание тяги на судах вращающимися вертикальными цилиндрами за счет силы ветра вместо парусов.

Моя работа разделена на две логические части: аналитическую и экспериментальную. В аналитической будут представлены теоретические выкладки по исследуемому явлению, а в экспериментальной – результаты экспериментов и их систематизация с помощью таблиц и графиков.

Обзор литературы

Эффект Магнуса достаточно популярная тема для научных работ. В работе «Эффект Магнуса» от авторов Бородина И.Д., Берестовой Е., Берестовой С.А., Войцык А. сила Магнуса теоретически рассматривается почти также, как и в моей работе, но экспериментальная часть другая: «Эффект Магнуса можно легко продемонстрировать при помощи опыта со скатыванием цилиндра по наклонной плоскости» [2]. Такой метод запуска не позволяет набрать цилиндру большую поступательную и угловую скорость, к тому же скорости жёстко связаны, а в моей работе их соотношение можно менять в момент запуска. Также полёт цилиндра ограничен высотой наклонной плоскости по отношению к нулевому уровню потенциальной энергии. В итоге, в этом опыте получается не петля, а лишь дуга окружности, которая не позволяет рассмотреть изменение влияние падения скоростей на форму траектории. В этой работе эксперимент производился с одинаковыми параметрами цилиндра и не были рассмотрены другие силы, действующие на тело, а нашей работе менялись масса, длина, момент инерции цилиндра; оценивались силы сопротивления и вязкого трения. Идея выполнения проведённого нами эксперимента взята из статьи «Эксперименты с эффектом Магнуса» журнала «Квант» [3].

В статье «Эффект Магнуса» И.Ю. Куликов критикует подход к вычислению подъёмной силы Эффекта Магнуса через уравнение Бернулли: «Невероятно большую аэродинамическую силу, возникающую при обтекании вращающегося цилиндра, Прандтль пытался объяснить на основе теоремы Бернулли, по которой давление в потоке жидкости или газа резко падает при увеличении скорости потока. Однако, такое объяснение мало убедительно, поскольку многочисленные аэродинамические опыты наглядно доказали, что падение давления на обтекаемой поверхности зависит от относительной скорости обтекания, а не от скорости потока» [1]. Мы согласны с Куликовым и добавим, что уравнение Бернулли вообще применимо только для невязкого газа, а рассмотрение пограничного слоя подразумевает учет вязкости. Но школьный уровень не позволяет придерживаться этого подхода. Мы использовали уравнение Бернулли, и оно правильно качественно описало наблюдаемые явления.

Основная часть

Экспериментальная часть

В качестве экспериментального цилиндра были использованы скреплённые донышками пластиковые стаканы (см. Рис. 2), позже конструкция была немного изменена для изучения изменений параметров полёта. Цилиндру сообщалась поступательная и вращательная скорость при стрельбе им, как из рогатки, после наматывания на него растянутого резинового жгута. При таком способе запуска цилиндра можно легко распределять энергию деформации резины между кручением и поступательным движением цилиндра. Полёт цилиндра регистрировался на мобильный телефон со скоростью съёмки 240 кадров в секунду. Видеоматериалы просматривались в режиме покадровой перемотки, что позволило зарегистрировать координаты цилиндра, время, а также период вращения вокруг своей оси с помощью метки на цилиндре.

Экспериментальные данные обрабатывались в программе MSExcel. Численно определялись скорость, ускорение, путь, а их зависимости от времени и от координаты автоматически аппроксимировались различными степенными законами. Всего было записано в видеорежиме пять траекторий:

• 1 и 2 (цилиндры одинаковы по параметрам, но разные поступательные и угловые скорости,

• 3 (масса и момент инерции увеличены в два раза за счёт вставки внутрь дополнительных стаканчиков при сохранении длины цилиндра) (рис. 3),

• 4 (масса и длина увеличены в два раза путём присоединения с торцов дополнительных стаканчиков) (рис. 4),

• 5 (масса увеличена в два раза при неизменном моменте инерции).

Аналитическая часть

Эффект Магнуса в моей работе рассмотрен для вращающегося вокруг своей оси цилиндра, который помимо угловой скорости имеет и поступательную. Подъёмная сила Эффекта Магнуса будет всегда перпендикулярна скорости и, благодаря этому, траектория полёта цилиндра будет напоминать петлю. Для оценки радиуса этой петли нужно подробно рассмотреть случай, когда цилиндр увлекает за собой прилегающие слои воздуха: воздух получает поступательную движение, а также вращается вокруг цилиндра. Из-за разности направлений поступательной и вращательной скорости образуются области, где результирующая скорость равна сумме этих скоростей и где результирующая скорость равна их разности (см. рис. 1).

Уравнение Бернулли гласит, что внутреннее давление газа или жидкости уменьшается с увеличением скорости. Применим этот закон к случаю с цилиндром. Оказывается, что в области с большей скоростью воздуха давление меньше, чем в области с меньшей скоростью. Из-за разности сил, действующих на цилиндр, и возникает подъёмная сила Магнуса. Также, воспользовавшись уравнением Бернулли, можно найти изменение давления при переходе из областей с разным давлением:

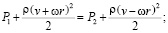
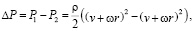
где ρ – плотность среды, ν – скорость потока, ω – угловая скорость цилиндра, r – радиус цилиндра, – давление в области большей скорости, – давление в области меньшей скорости.

Подъёмная сила Магнуса рассчитывается по формуле

,

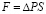где S – площадь горизонтальной проекции цилиндра. Подставим уже найденное изменение давления и площадь поверхности цилиндра:

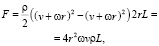
где L – длина цилиндра, ω – угловая скорость цилиндра.

Из наблюдений видно, что цилиндр описывает петлю. В простейшем случае можно представить петлю окружностью. Тогда, если пренебречь силами сопротивления, вязкого трения и силой тяжести, то в системе координат центра масс цилиндра вдоль радиуса кривизны траектории действует центробежная сила против силы Магнуса:

.

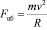Т.к. F=Fцб => ,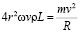

где m – масса цилиндра.

Из этого уравнения можно вывести радиус окружности:

.

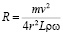Если же учесть реальное уменьшение поступательной и угловой скорости, то, из-за разных темпов их изменений, радиус окружности может изменяться.

Уменьшение поступательной скорости связано с наличием сил аэродинамического сопротивления

,

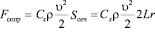где Сx – аэродинамический коэффициент, характеризующий форму тела с точки зрения её обтекаемости, Sсеч – площадь сечения цилиндра.

Запишем 2-й закон Ньютона:

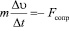
или в безразмерных величинах

.

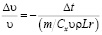Понятно, что знаменатель в правой части имеет размерность времени – это характерное время процесса. Однако, вместо неопределенной текущей скорости надо подставить известную величину начальной скорости

.

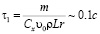Заметим, что существует точное решение исходного уравнения, правда, выходящее за рамки школьной программы:

,

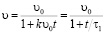из которого характерное время уменьшения скорости в 2 раза в точности совпадает с предложенной нами оценкой

.

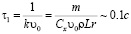Уменьшение угловой скорости связано с наличием вязкого трения (надо учитывать внешнюю боковую поверхность цилиндра и внутреннюю, т.к. цилиндр с торцов открыт):

,

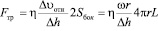где Δh – толщина пограничного слоя, η – коэффициент вязкого трения.

Данная сила направлена по касательной против вращения цилиндра относительно его оси симметрии. Сила трения создает момент силы, который уменьшает момент импульса вращения цилиндра:

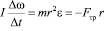
(I – момент инерции). Или в относительных единицах

.

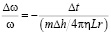В знаменателе правой части стоит величина, имеющая размерность времени. Можно принять ее за характерное время процесса. Действительно, точное решение данного уравнения (выходящее за школьные рамки) имеет вид:

,

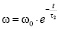где характерное время

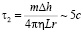
(при 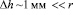и η=17,1 мкПа•с) соответствует уменьшению угловой скорости закрутки в 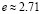раз.

Объяснение экспериментов

Анализ видеоматериалов эксперимента показал, что траектория движения представляет собой не окружность, а петлю неправильной формы или скручивающуюся плоскую спираль со сдвигом, т.е. со временем радиус окружности уменьшается, а ее центр сдвигается. Но несмотря на это, сравнение результатов полётов разных цилиндров даёт возможность проверить состоятельность выведенных формул.

Из графиков 1 и 2 (см. рис. 5) видно, что запуск одного и того же цилиндра при разном натяжении резинового шнура (с разными линейными 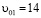м/с 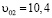м/с и угловыми 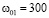рад/с, 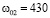рад/с начальными скоростями (см. табл. 1)) приводит к изменению размеров петель – с 5 см до 4.5 см в горизонтальном направлении или с 14 см до 11 см в вертикальном. Действительно, если сопоставить значения линейных и угловых скоростей цилиндра в верхних точках петель (см. рис. 10, табл. 1(верхние точки выделены чёрным цветом)), то отношение v/ω уменьшается с 1.13 (м/с) /301.4 (рад/с) =0.00375 до 0.94 (м/с) /318 (рад/с)=0.00296 или в 1.3 раз. Это теоретически качественно объясняет уменьшение радиуса окружности согласно формуле

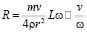
Из графиков 2 и 5 (см. рис. 6) видно, что, увеличивая массу цилиндра примерно в 2 раза (с 5.6 до 11.2 грамм) (при прочих равных условиях, к которым относится и момент инерции) мы увеличиваем радиус петли с 4.5 см до 7 в горизонтальном направлении или с 11 см до 13 см в вертикальном. Этот эффект предсказывает качественно в упрощенном виде и наша формула 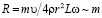. Отметим, что начальные скорости (см. табл. 1) в этом сравнении были одинаковы: линейные v0 = 10,4 м/с и угловые ω0=430 рад/с.

Интересно отметить, что в случаях 4 и 5 (см. рис. 8), вопреки внесенным изменениям, угловые скорости ведут себя одинаково (равны их начальные значения и значения в вершинах петель), что объясняется компенсацией увеличения длины образующей цилиндра закрытием его торцов в случае 4, т.е. внутренняя боковая поверхность не участвует в создании момента трения (см. рис. 4).

Случай 3 не был сравнён с другими, потому что форма траектории сильно отличалась от других петель (см. рис. 7). Возможно, это произошло из-за сильно возросшего момента инерции.

Довольно большие значения начальной поступательной и, особенно, начальной угловой скорости цилиндра вызвали у нас определенное недоверие к измерениям в эксперименте. Была предпринята косвенная проверка полученных данных путем подсчета затрат энергии и их сравнения с энергией деформации резинового жгута. Должно выполняться Wдеф >Wкин (Wдеф – энергия деформации резинового жгута, Wкин – кинетическая энергия цилиндра). Рассчитаем начальную кинетическую энергию поступательного и вращательного движения цилиндра:

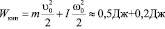
(для первой траектории) или 0,27 Дж+0,42 Дж (для второй траектории). Получились величины сопоставимые между отдельными видами энергий, уже это укрепляет уверенность в правильности определения угловой скорости. Однако, дополнительно была определена жесткость резинового шнура и его растяжение при запуске цилиндра: k≈17 H/м, Δx≈35 см. Энергия деформации составила

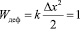Дж.

Таким образом, баланс энергий был соблюден и измерения следует признать корректными.

Также экспериментальные данные объясняют отсутствие второй петли у цилиндра. По результатам вычислений, оказывается, что в конце петли сила Магнуса сопоставима с силой тяжести цилиндра (см. табл. 2). Также в таблице (см. табл. 2) есть значения силы сопротивления, которая в начале движения должна быть равна произведению массы цилиндра и его ускорения. Чтобы проверить правильность приведённых значений вычислим ускорение в начале движения:

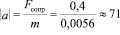м/с2

Значение начального ускорения из графика для траектории 2 (см. рис. 13), ложащегося на линию тренда, по модулю равно 85 м/с2. Значения отличаются относительно не сильно, следовательно, можно судить о правильности выполнения измерений и вычислений.

Графики зависимостей поступательной скорости, угловой скорости, ускорения от времени были построены в программе «Excel» на основе вычисленных там же значений. Скорость вычислялась, как отношение перемещения (находилось через теорему Пифагора по координатам цилиндра) к времени, за которое оно совершалось. Ускорение находилось, как изменение скорости (разность скоростей) к времени, за которое оно произошло. Угловая скорость вычислялась через период обращения цилиндра вокруг своей оси по формуле . Путь находился, как сумма путей между двумя ближайшими точками, которые вычислялись, как произведение скорости цилиндра и времени. Все величины вычислялись итерационно, т.е. по предыдущему значению вычислялось последующее на каждом временном шаге.

Техническое применение

Проблема аэродромов малой авиации в России остаётся актуальной уже много лет. Одним из способов её решения является уменьшение затрат на строительство взлётно-посадочной полосы. Я предлагаю сократить длину разбега и пробега самолётов лёгкой авиации при помощи конструкции, разработанной на основе моих исследований Эффекта Магнуса.

Основным элементом конструкции являются трёхсекционные телескопические выдвижные цилиндры с каждой стороны (L=1,5 м, R=0,25 м). Для уменьшения силы трения, препятствующей вращению, и силы сопротивления (особенно на взлете), создающей значительные механические нагрузки на конструкцию, цилиндры необходимо делать закрытыми с торцов. Каждая секция цилиндра должна иметь выступающее оребрение для увеличения жесткости и препятствия перетеканию вихрей. Масса цилиндров из углепластика при толщине стенки 2мм примерно 30 кг. При частоте вращения конструкции 40 оборотов в секунду, создается сила Магнуса 3600Н (полезная часть силы 3300Н). Т.е. на ~13 % (Eclipse 500) или на 8 % (Ан-28 (рис. 15)) от исходной величины можно понизить подъемную силу основного крыла. Начальная скорость пробега/скорость отрыва при взлете связаны с дистанцией следующей формулой 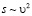. Подъемная сила основного крыла также зависит от скоростного напора по формуле 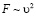, а сила Магнуса выдвижных цилиндров при закручивании от мотора – 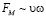. Отсюда видно, что при фиксированной частоте закрутки выгодно использовать силу Магнуса именно при низких скоростях, когда ее относительный вклад выше. При уменьшении на 13 % подъемной силы дистанция также должна сократиться на 13 % даже без учета возросшего аэродинамического сопротивления самолета (выдвижные цилиндры дополнительно выполняют функцию тормозных щитков). С учетом последнего фактора дистанция пробега сократится еще сильнее. Подъемной силой и тормозящим эффектом цилиндров можно управлять за счет изменения их длины и частоты вращения.

Выводы

В ходе проведённого исследования были получены качественные зависимости изменения радиуса петли от таких характеристик: скорости, угловой скорости, длины цилиндра, радиуса цилиндра, плотности среды. Эти данные могут послужить, как и для изучения Эффекта Магнуса в школьной программе, так и для использования в аэро- и гидродинамических исследованиях.

Полученные данные помогли сформулировать практическую рекомендацию: подъёмную силу Эффекта Магнуса энергетически выгоднее развивать за счёт увеличения частоты вращения, нежели за счёт увеличения поступательной скорости, т.к. линейная скорость затухает быстрее угловой, а сила аэродинамического сопротивления больше силы вязкого трения.

Данная рекомендация может быть применима для увеличения подъёмной силы летательных аппаратов во время взлёта и посадки с помощью вращающихся цилиндров в качестве переднего горизонтального оперения. Используя такую конструкцию, можно понизить поступательную скорость самолёта, сохранив или увеличив подъёмную силу. Также важным преимуществом такой конструкции является уменьшение длины взлёта и пробега.

Приложение

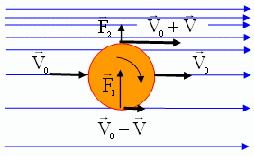
Рис. 1. Возникновение подъемной силы, действующей на тело, помещенное в газовый поток (эффект Магнуса)

Рис. 2

Рис. 3

Рис. 4

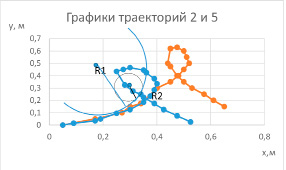
Рис. 5. Точки старта, то есть отделения цилиндра от резинки, совмещены. Синияя линия – траектория 5, орнажевая – траектория 2

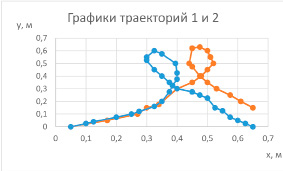
Рис. 6. Точки старта, то есть отделения цилиндра от резинки, совмещены. Синяя линия-траектория 1, орнажевая-траектория 2

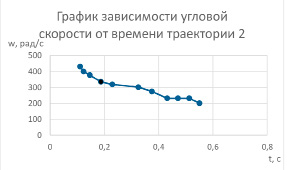
Рис. 7

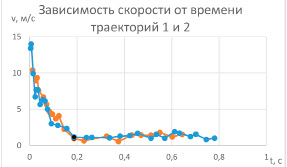
Рис. 8

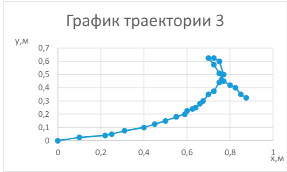
Рис. 9

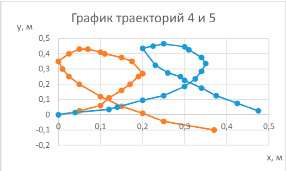
Рис. 10. Точки старта, то есть отделения цилиндра от резинки, совмещены. Оранжевая линия-траектория 4, синяя-траектория 5

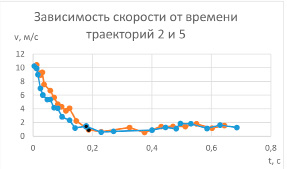
Рис. 11. Точки старта, то есть отделения цилиндра от резинки, совмещены

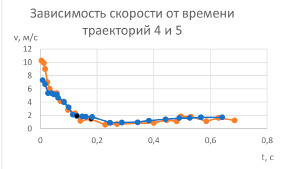
Рис. 12

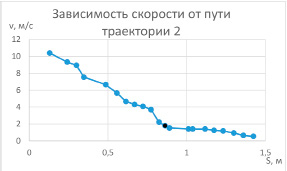
Рис. 13

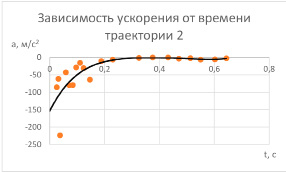
Рис. 14. Чёрная линия – полиноминальная (5 степени) линия тренда

Рис. 15

Таблица 1

Таблица 2

Силы, действующие на цилиндр во втором случае

Библиографическая ссылка