Введение
Тема моей исследовательской работы «Графический способ решения систем алгебраических уравнений с использованием программного пакета MathCAD».
Данная научно-исследовательская работа является актуальной в силу четырех обстоятельств:
1.Она имеет непосредственное практическое отношение к курсу алгебры в школе;
2.Элементы работы могут быть представлены для изучения учащимся 8-11 классов;
3.Возможность применения программного пакета MathCAD для проверки знаний учащихся, связанных связанная с графическим решением систем алгебраических уравнений;
4.Работа имеет прикладной характер и требует изучения языка программирования MathCAD;
Цель научно-исследовательской работы: показать применение программного пакета MathCAD для решения системы двух линейных уравнений с двумя переменными графическим методом.
Графический способ решение систем алгебраических уравнений лежит в основе исследования элементарных функций в курсе математики средней школы. График функции используют для решения задач и систем уравнений. В связи с этим данная работа позволит учащимся средней и, в особенности, старшей школы более плодотворно подготовиться к экзаменам и освоить решение систем алгебраических уравнений графическим способом, изучаемых в школе.
Для достижения цели были поставлены следующие задачи:
Изучить процесс построения графиков алгебраических уравнений в курсе средней школы;
Изучить функционал среды программирования MathCAD;
и ее возможности;
Изучить основы программирования на языке Pascal;
Научно-исследовательская работа состоит из: введения, двух глав, заключения и списка литературы.
В введение сформулированы цель, задачи и актуальность научно-исследовательской работы.
В первой главе рассмотрен функционал среды инженерного программного пакета MathCAD и его возможности для графического способа решения систем алгебраических уравнений.
Во второй главе рассмотрен алгоритм графического метода решения систем линейных уравнений с помощью программы MathCAD.
В заключении отражены результаты и перспективы применения программы MathCAD при графическом решении систем алгебраических уравнений на уроке алгебры.
В работе рассматривается тематика, связанная с решением систем алгебраических уравнений с применением программного продукта MathCAD
Использование компьютерных программ для построения графиков функций и уравнений, изучение их свойств и закономерностей, дает возможность рассмотреть большое количество примеров с минимальными затратами времени. Данная работа предназначена в помощь учителям при изучении построения графиков функций, заданных уравнениями выше второй степени, а также ученикам с целью заинтересовать их математикой и информатикой, показав возможности использования информационных технологий на уроках математики.
Глава 1. Среда программирования MathCAD для построения графиков линейных уравнений.
Материал данной главы взят из учебного пособия «Использование пакета Mathcad в информатике». [1]
На рис. 1 приведены основные команды меню пакета Mathcad 15, та-
кие как Файл – Правка – Вид – Добавить – Формат – Инструменты – Символика – Окно – Справка.
Рис. 1 Интерфейс окна Mathcad
Для удобства работы можно устанавливать панели инструментов:
Стандартная, Форматирования, Математика и т. д. Некоторые из них (Вычисления, Математика, Греческий алфавит, График, Вектор и матри-
ца, Исчисление, Математический анализ, Логика, Греческие буквы, Символика, Программирование, Модификаторы) приведены на рис.2
Рис. 2 Основные панели инструментов
Основные типы данных
Алфавит системы содержит:
· строчные и прописные буквы латинского алфавита;
· строчные и прописные буквы греческого алфавита;
· арабские цифры от 0 до 9;
переменные
(TOL, ORIGIN, PRNPRECISION, PRNCOLWIDHT, FRAME);
· имена встроенных функций;
· специальные знаки;
Системные переменные имеют определенные системой значения, например TOL – погрешность численных методов, по умолчанию равна
0.001. Её можно изменять путем присвоения нового значения.
Функции решения алгебраических уравнений и систем Find(x,y,...) – возвращает значения х, у, …, удовлетворяющие ограничениям: равенствам и неравенствам, которые определены в блоке решения уравнений.
Maximize(f,var1,var2,...) – возвращает значения var1, var2, которые обеспечивают максимальное значение функции f. Перед использованием этой функции необходимо задать начальное приближение для каждой неизвестной, и если ограничения даны, то ключевое слово – Given.
Minerr(x,y,...) – возвращает значения x, y, ..., наиболее близкие к решению системы уравнений; х и у есть скалярные переменные, значения которых ищутся в системе уравнений. Перед использованием этой функции необходимо задать начальное приближение для каждой неизвестной, и если ограничения даны, то ключевое слово – Given.
Minimize(f,var1,var2,...) – возвращает значения var1, var2, которые обеспечивают минимальное значение функции f. Перед использованием этой функции необходимо задать начальное приближение для каждой неизвестной, и если ограничения даны, то ключевое слово – Given.
Root(f(x),x) – находит корень уравнения с одним неизвестным.
Организация циклов
Для организации цикла необходимо набрать переменную, присвоение, константу начала, две точки как символ циклических действий и константу конца. Если константа начала больше константы конца, то шаг равен –1, иначе шаг равен 1 Если после константы начала поставить запятую константу, то шаг равен разности между стартовым значением и следующим. Переменные, которые могут иметь множество регулярных значений, называются ранжированными (от слова range variable).
Вводим x: 0 ; 5
получаем: х:=0..5,
шаг равен 1
Если начальное значение больше конечного (x:=5..0), то шаг равен –1.
x:=2,2.5..4 – шаг равен 0.5. Начальное значение 2
Система линейных алгебраических уравнений
Для численного решения линейных систем уравнений в Mathcad имеется специальная функция lsolv(A,B). Она решает систему линейных алгебраических уравнений вида А×X = B, выдавая решение – вектор X.
А – матрица коэффициентов размерности n×n; В – вектор свободных членов размерности n; X – вектор неизвестных пока решений.
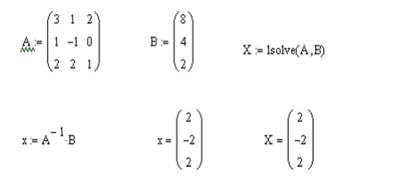
Или простым матричным методом:
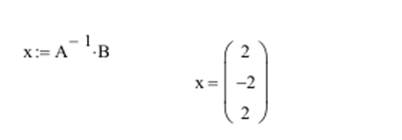
Глава 2. Алгоритм графического метода решения систем линейных уравнений с помощью программы MathCAD.
1.1 Алгоритм построения графика линейного уравнения с помощью программы MathCAD;
Пример1.
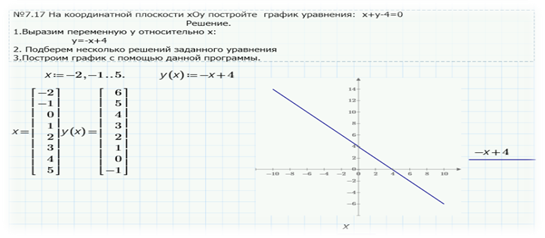
На координатной плоскости хОу постройте график уравнения:
а) х+у-4=0
Выполнение задания:
1.Задать функцию, приведенную выше. Вставить оператор абсолютного значения
2.На вкладке Графики в группе Кривые щелкнуть Вставить график, а затем выбрать График ХУ.
Появиться пустой пустой график
3.В местозаполнителе оси У ,в левой или правой части ввести функцию
у = -х+4.
4.В местозаполнителе оси Х внизу графика ввести х. Нажать клавишу «Ввод», появиться линейная кривая.
Пример 2.
Постройте график линейной функции у = х+4 и у=2х
Найдите:
а) координаты точек пресечения графика с осями координат;
б) значение у, соответствующее значению х=--2;-1;1.
в ) значение х ,которому соответствует значение у, равное-2;2;4.
Алгоритм построения
1. Задать функцию, приведенную выше. Вставить оператор абсолютного значения
2. На вкладке Графики в группе Кривые щелкнуть Вставить график, а затем выбрать График ХУ
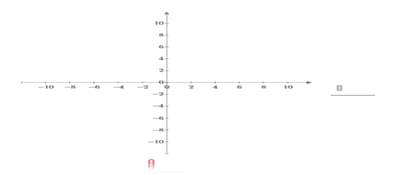
Появиться пустой график.
3. В местозаполнителе оси У ,в левой или правой части ввести функцию у = х+4.
4. В местозаполнителе оси Х внизу графика ввести х. Нажать клавишу «Ввод», появиться линейная кривая
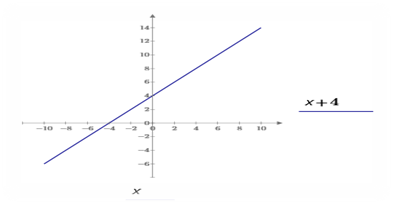
5.Установить курсор справа от функции. Щелкнуть Добавить кривую.
Появиться новый местозапонитель оси У под текущим местозаполнителем.
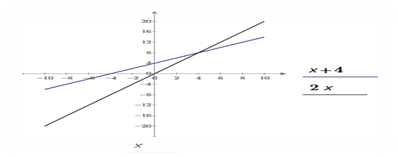
а) Найти координаты точек пресечения графика с осями координат.
На графике точки пересечения: х=0,у=- 4 :У=0,х=4
б) Найти значение у, соответствующее значению х = --2;-1;1.
в) Найти значение х которому соответствует значение у, равное-2;2;4.
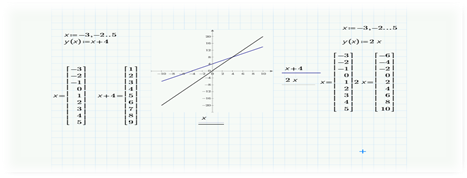
Внесем данные и получим следующее распределение по столбцам .
1.2.Алгоритм графического метода решения систем линейных уравнений с помощью программы MathCAD;
Пример 1. Решить систему уравнений
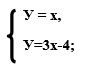
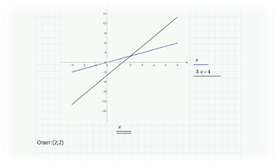

Ответ: система имеет одно решение (2;2)
Пример2.
Решить систему уравнений
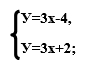
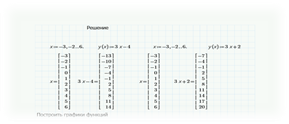
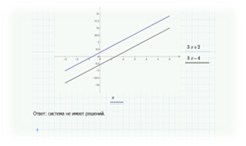
Ответ: система не имеет решений
Заключение
Работая над научно-исследовательской работой, мне пришлось изучить учебно-методическую и научную литературу, а также проанализировать материал, изученный мной в школе.
В процессе исследования:
-из множества программ, позволяющих рисовать графики функций, выполнять построения, была выбрана MathCAD , которая является средой визуального программирования, то есть не требует знания специфического набора команд. Простота освоения пакета, дружественный интерфейс, относительная непритязательность к возможностям компьютера явились главными причинами того, что именно этот пакет был выбран мной для решения данной проблемы;
- изучил алгоритм построения графика линейного уравнения с помощью программы MathCAD;
- изучил графический метод решения систем линейных уравнений с помощью программы MathCAD и убедился в том, что графический метод решения системы линейных уравнений имеет большое значение при подготовке к ОГЭ и ЕГЭ..
С помощью программы MathCAD мною были выполнены все задания из задачника Алгебра 9 класс по этой теме, ряд заданий олимпиадного характера и задания для подготовки к ОГЭ. Я смог за короткий срок выполнить большой объем учебного материала, причем в очень наглядной и доступной форме.В процессе работы не тратил время на составление таблиц и построение графиков в тетради .Получился большой запас времени на отработку заданий повышенной сложности.
