Цель деятельности учителя
Создать условия для совершенствования навыков решения тригонометрических уравнений
Планируемые результаты
• Предметные умения: Умеют применять изученные понятия, методы для решения задач
• Универсальные учебные действия:
– Познавательные: осуществляют логические действия; формулируют ответы на вопросы.
– Регулятивные: умеют самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных задач, адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность и собственные возможности ее решения.
– Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве.
– Личностные: имеют целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики
План урока
I. Актуализация знаний
Цель деятельности: проверить уровень сформированности знаний по теме простейшие тригонометрические уравнения, подготовить к восприятию нового.
1. Теоретический опрос. (Индивидуально подготовить ответы на вопросы)
1 ученик: на крайней левой стационарной доске
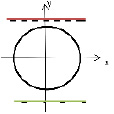
Изобразить схемы решения уравнений вида: cоs x =a
Ответ:
Если │а│≤1, то cоs x =a имеет решения вида
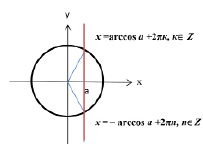
Если │а│>1, то cоs x =a
Решений нет
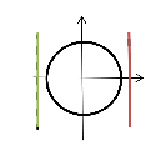
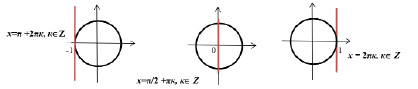
2ученик: на крайней правой стационарной доске
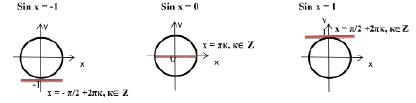
Изобразить схемы решения уравнений вида: Sin x =a
Ответ:
Если │а│≤1, то sin x =a имеет решения вида Если │а│>1, то sin x =a
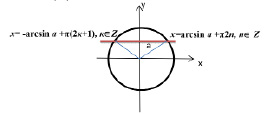
Множество решений можно записать так: решений нет
х=(–1)narcsin x +πk, k∈ Z.
3 ученик: на центральной части стационарной доски.
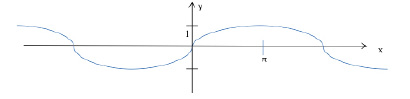
Начертить график функции у = sin x/2
Ответ
4 ученик: на центральной части стационарной доски или на дополнительной маркерной доске.
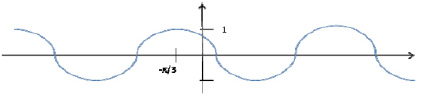
Начертить график функции у = cos (x +π/3)
Ответ
2. Фронтальная работа с классом (на интерактивной доске задание в виде таблице) Устная работа.
В каждом из приводимых примеров селаны ошибки. Заполните схему. Напишите верный ответ. Подумайте о причине ошибки (обучающиеся заполняют 3 и 4 столбики таблицы)
|
Пример |
Ответ с ошибкой |
Схема |
Верный ответ |
|
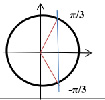
cos x = 1/2 |
X=±π/6 +2πk, k∈Z |
|
x=±π/3 +2πk, k∈Z |
|
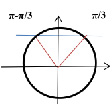
sin x = √3/2 |
x=π/3 +πk, k∈Z |
|
x=π/3 +2πk, k∈Z x=2π/3 +2πk, k∈Z |
|
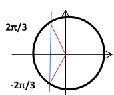
cos x = – 1/2 |
x=±π/3 +2πk, k∈Z |
|
x=±2π/3 +2πk, k∈Z |
|
sin x = √10/3 |
x=(–1)ⁿarcsin √10/3+ πk, k∈Z |
|
√10/3 > 1, то решений нет |
|
Cos x = π/4 |
x ∈ Ø |
Т.к π/4≤1, то |
x= ±arccos π/4+ 2∏ k, |
3. Проверить ответы учащихся у доски.
II. Изучение новой темы. Совместная деятельность
Цель деятельности: Вывести алгоритм решения уравнений вида sin f(x) = a, cos f(x)=a.
Сегодня мы с вами должны освоить методы решения тригонометрических уравнений вида sinf(x) = a, cos f(x)=a.
1. Я предлагаю вам решить вместе следующее уравнение: sin x/2= – 1/2.
Пример на интерактивной доске
Можно ли данное уравнение решить графическим способом?
Графики каких функций для этого необходимо начертить?
График какой функции сегодня мы уже построили на доске?
Так как, на доске уже построен график у = sin x/2, нам остаётся построить только график какой функции?
y = –1/2
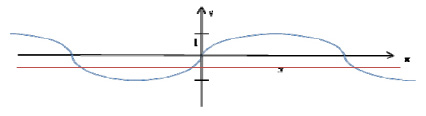
Какой вывод можно сделать?
Ученики. Данное уравнение имеет бесконечное множество решений.
Скажите, чем наше уравнение отличается от простейшего, умеем ли мы с вами решать простейшее тригонометрическое уравнение?
Какое действие поможет данное уравнение превратить в прстейшее тригонометрическое уравнение?
Правильно, ввести новую переменную?
Давайте попробуем это сделать. Вызываем к доске обучающегося и решаем вместе данное уравнение.
sin x/2= – 1/2.
Пусть x/2=t, тогда получим sin t = – ½
t = (-1)ⁿ arcsin (-1/2)+ πk, k∈Z,
t = (-1)ⁿ⁻¹ π/6+ πk, k∈ Z
x/2 = (-1)n–1 π/6+ πk, k∈ Z
x= (-1)ⁿ⁻¹ π/3+ 2πk, k∈Z
Ответ: x= (-1)ⁿ⁻¹ π/3+ 2πk, k∈Z
Попробуйте сформулировать алгоритм решения уравнений вида sin f(x) = a, cos f(x)=a.
1. Решить сначала уравнение относительно f(x), как простейшее тригонометрическое уравнение.
2. Полученное уравнение решить относительно x.
2. Решить уравнение (учащийся у доски).
cos (x +π/3) = 1
(x +π/3)=2πk, k∈ Z
x = –π/3 +2πk, k∈ Z
Укажите несколько решений данного уравнения
При k =0, x = –π/3
При k=1, x = –π/3 +2π= 5π/3
При k= –1, x = –π/3 –2π= – 7π/3
Учитель показывает данные ответы с помощью построенного графика в начале урока.

3. Работа в парах. Решите данное уравнение по выработанному алгоритму. Подумайте можно ли данное уравнение упростить?
III. Проверка решений учащихся
Библиографическая ссылка
Ярчук И.В. УРОК. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ ВИДА SIN F(X) = A, COS F(X)=A // Международный школьный научный вестник. 2019. № 4-4. ;URL: https://school-herald.ru/ru/article/view?id=1215 (дата обращения: 04.03.2026).