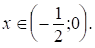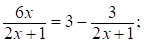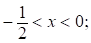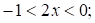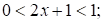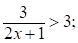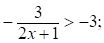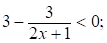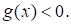Великий математик Карл Фридрих Гаусс, в свое время, назвал математику «царицей всех наук». Математика скорее добрая фея, только получить у нее можно не волшебную палочку, а надежный и точный инструмент – математические методы.
И.Г. Петровский
Реализация концепции математического образования Российской Федерации, утвержденной приказом Минобразования России от 24.12.2013 г. № 2506-р, направлена на более эффективную подготовку выпускников школы к освоению программ высшего профессионального образования.
В связи с чем, мы посчитали необходимым рассмотреть использование некоторых свойств функций (область определения, ограниченность, монотонность) при решении нестандартных неравенств, как один из эффективных методов подготовки будущих абитуриентов.
Пример 1. (Демовариант ЕГЭ-2015, задание 17)
Решите неравенство:
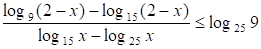 .
.
Решение
1. ОДЗ: 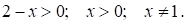
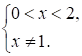
2. а) При 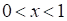 имеем
имеем
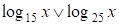
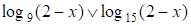
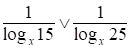
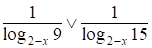
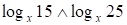
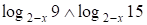
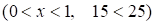

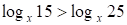
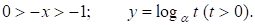
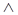 ~
~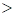 ;
; 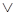 ~
~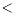 .
. 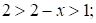 возр. ф.)
возр. ф.)
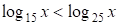 .
. 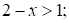
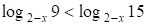
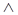 ~
~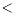 ;
;  ~
~ .
.
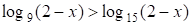 .
.
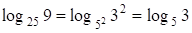 ;
; 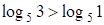 ;
; 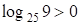 .
.
Левая часть неравенства отрицательна, правая часть неравенства положительна; (0; 1) – множество решений.
б) При 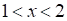 имеем
имеем
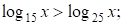
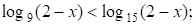
левая часть неравенства отрицательна, 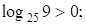 (1; 2) – множество решений неравенства.
(1; 2) – множество решений неравенства.
в) 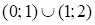 - множество всех решений данного неравенства.
- множество всех решений данного неравенства.
Ответ: (0; 1); (1; 2).
Пример 2 (Пробник 2015, задание 17)
Решите неравенство 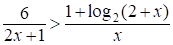 .
.
Решение.
1. ОДЗ: 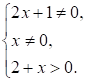
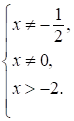
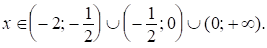
2. а) При 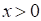 имеем
имеем
умножим обе части неравенства на х
(*) 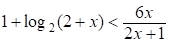 ; где
; где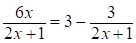 .
.
Правая часть неравенства (*) строго меньше 3 при 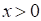 .
.
Пусть 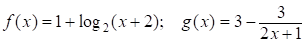 .
.
Функции f и g – возрастающие функции.
Если 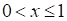 , то
, то
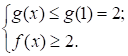 значит, неравенство
значит, неравенство 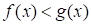 не имеет решений.
не имеет решений.
|
Если
где Значит, неравенство |
|
Если 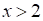 , то
, то
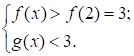 значит, неравенство
значит, неравенство 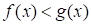 не имеет решений.
не имеет решений.
б) При 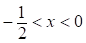 имеем
имеем
умножаем обе части на x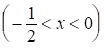 , получаем равносильное неравенство
, получаем равносильное неравенство 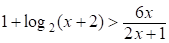 .
.
|
|
|
в) При 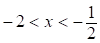 имеем
имеем
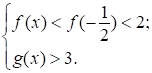
Значит, неравенство 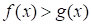 не имеет решений.
не имеет решений.
Ответ: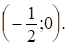
Таким образом, для обеспечения устойчивого повышения уровня успеваемости учащихся необходимо обратить внимание, прежде всего, на развитие таких структур интеллекта, как математическая интуиция, формально-логическое мышление, оперативная логическая память.
Одним из путей формирования УУД может стать включение таких заданий в содержание обучения математике (например, в рамках элективного курса).
Библиографическая ссылка
Караева Д.А. НЕСТАНДАРТНЫЕ НЕРАВЕНСТВА // Международный школьный научный вестник. 2021. № 6. ;URL: https://school-herald.ru/ru/article/view?id=1495 (дата обращения: 10.01.2026).

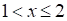 , то
, то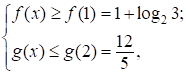
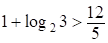 .
.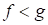 не имеет решений.
не имеет решений.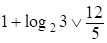
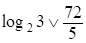
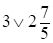
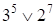
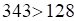
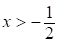
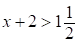
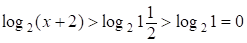 ;
;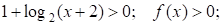
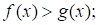 верно при любом
верно при любом